
Qu’est-ce qu’une suite de nombres réels ?…
L’illustration dynamique ci-dessous peut en donner une première idée.
Une suite de rebonds …
Une balle est lâchée sans vitesse initiale et rebondit indéfiniment.
A chaque rebond, elle perd un peu d’énergie par dissipation : friction avec le sol, déformation et échauffement de la balle et du support, émission d’ondes sonores, resistance de l’air, …
Notons :
 la hauteur de laquelle la balle est lâchée,
la hauteur de laquelle la balle est lâchée, la hauteur atteinte à l’issue du n-ème rebond, pour
la hauteur atteinte à l’issue du n-ème rebond, pour 
Les nombres ![]()
![]()
![]() etc … forment une suite de nombres positifs.
etc … forment une suite de nombres positifs.
Dans le monde réel, la balle finira bien sûr par s’immobiliser, ce qui suggère de ne considérer qu’une liste (une suite finie). Mais on peut aussi considérer que ![]() est défini pour tout n, et que
est défini pour tout n, et que ![]() dès que n est assez grand.
dès que n est assez grand.
L’objet de cet article est de montrer comment on étudie une suite numérique, sur le plan qualitatif : sens de variation, caractère borné ou non, convergence ou divergence, périodicité éventuelle … tout en se limitant à des outils accessibles en fin de lycée.
Dans un premier temps, les notions utiles sont introduites (sections 1 à 5). En fin d’article, des exemples variés sont examinés en détail.
1 – Quel est le terme suivant ?
L’un des tests de logique les plus connus consiste, après avoir énuméré quelques nombres, à demander quel doit être le suivant. Connaissant les premiers termes ![]() d’une certaine suite numérique, il faut donc tâcher de trouver
d’une certaine suite numérique, il faut donc tâcher de trouver ![]()
Dans certains cas, une réponse s’impose plus que toute autre … Par exemple, en démarrant avec :
1, 2, 4, 8, 16, 32
on reconnaît les premières puissances de 2; il est donc raisonnable de proposer 64 pour le terme suivant.
De même, l’énumération :
2, 3, 5, 7, 11, 13, 17, 19, 23
doit faire penser aux nombres premiers. C’est donc 29 qui est probablement attendu ensuite.
Dans certains cas, si aucune règle supplémentaire n’est fixée, alors plusieurs réponses sont envisageables, toutes aussi acceptables les unes que les autres. On peut consulter l’exemple du nombre de régions limités par les cordes joignant ![]() points d’un cercle, qui est présenté dans cet article et le comparer avec celui des puissances de 2.
points d’un cercle, qui est présenté dans cet article et le comparer avec celui des puissances de 2.
Voici un troisième exemple, plus original …
Quel serait, selon vous, le terme suivant pour la séquence ci-dessous ?
2, 5, 4, 3, 4, 3, 7, 5, 10, 9, 8, 9, …
Réponse (cliquer pour déplier / replier)
Vous cherchiez sans doute une astuce arithmétique ou une formule ?
En fait, cette suite a été construite selon un procédé non mathématique. On a simplement énuméré, dans l’ordre croissant, les entiers positifs dont l’écriture en toutes lettres (et en français) ne comporte pas la lettre ‘e’, en comptant à chaque fois le nombre de lettres (et sans compter le tiret éventuel) :

🙂
Bref, la donnée des premiers termes d’une suite numérique ne suffit pas pour connaître les suivants ! Il faut s’y prendre autrement pour définir une suite sans ambiguïté. De quelle manière ?
2 – Définir une suite … oui, mais comment ?
Les modalités les plus courantes sont :
- une formule explicite,
- une formule de récurrence.
➣ Une formule explicite permet le calcul direct d’un terme, dès que son indice (c’est-à-dire son numéro d’ordre) est connu. On peut faire démarrer les indices à zéro, ou bien à une autre valeur; c’est sans importance.
Par exemple, la formule explicite :
![]()
1, 2, 5, 10, 17, 26, 37, 50
La formule suivante :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace t_{n}=\left(\sum_{k=1}^{n}\frac{1}{k}\right)^{2}\prod_{k=1}^{n}\left(1-\frac{1}{2k^2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01ad46ad4148bb842825dc88c82dd18b_l3.png)
![]()
➣ Une formule de récurrence du premier ordre donne accès à n’importe quel terme, dès qu’on connaît celui qui le précède. Un exemple :
![]()
![]()
0, 1, 2, 5, 26, 677, 458330, 210066388901
Cette suite et la précédente sont distinctes, mais elles ont quelque chose en commun : les termes de la seconde sont tous présents dans la première (ce qui est normal, vu que ce sont des carrés d’entiers auxquels on a ajouté 1). En outre, l’ordre d’apparition des termes est le même : on dit que la seconde suite est extraite de la première.
➣ Une formule de récurrence du second ordre permet le calcul de chaque terme, dès que les deux précédents sont connus. Bien entendu, on a besoin des deux premiers termes pour amorcer le
processus. Exemple :
![]()
2, 1, 3, 4, 7, 11, 18, 29
Cette suite est connu sous le nom de suite de Lucas, c’est un peu la sœur jumelle de la suite de Fibonacci, quoique sans doute moins célèbre.

Les deux suites obéissent à la même formule de récurrence, mais avec des conditions initiales différentes. La suite de Fibonacci est définie par :
![]()
![]()
➣ On peut généraliser … Voici une suite définie par une relation de récurrence d’ordre 4 :
![]()
![]()
➣ Il faut également signaler le cas des suites définies par une formule de récurrence forte : on donne le premier terme ainsi qu’une formule permettant de calculer chaque terme en fonction de tous les précédents. Exemple :
![Rendered by QuickLaTeX.com \[\boxed{y_{0}=1\qquad\text{et}\qquad\forall n\in\mathbb{N},\thinspace y_{n+1}=1+\prod_{k=0}^{n}y_{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f6af3850e8a361ee3ed5a45fd2bdef78_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{ccccc}y_{0} & = & 1\\y_{1} & = & 1+1 & = & 2\\y_{2} & = & 1+1\times2 & = & 3\\y_{3} & = & 1+1\times2\times3 & = & 7\\y_{4} & = & 1+1\times2\times3\times7 & = & 43\\y_{5} & = & 1+1\times2\times3\times7\times43 & = & 1807\\y_{6} & = & 1+1\times2\times3\times7\times43\times1807 & = & 3263443\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec815413a9c529107cc20160c8be429f_l3.png)
En effet, si l’on pose :
![]()
![Rendered by QuickLaTeX.com \[\begin{array}{ccccc}z_{1} & = & 2^{2}-2+1 & = & 3\\z_{2} & = & 3^{2}-3+1 & = & 7\\z_{3} & = & 7^{2}-7+1 & = & 43\\z_{4} & = & 43^{2}-43+1 & = & 1807\\z_{5} & = & 1807^{2}-1807+1 & = & 3263443\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df05591a28dad92e505078df5c02268e_l3.png)
La suite ![]() est connue sous le nom de suite de Sylvester.
est connue sous le nom de suite de Sylvester.
Elle possède des propriétés remarquables. Par exemple, si l’on calcule la somme des inverses des premiers termes :
![]()
3 – Divers attributs pour une suite
L’illustration dynamique ci-dessous doit aider à rendre intuitives les notions de suite croissante, décroissante, stationnaire, oscillante, majorée, minorée, bornée, périodique, convergente … Des définitions précises sont données juste après (la convergence est définie à la section 4).
Cliquer sur l’image pour faire défiler les différents exemples :
Considérons une suite numérique ![]() (on peut noter
(on peut noter ![]() mais il est plus commode de noter simplement
mais il est plus commode de noter simplement ![]() .
.
![]() est dite croissante lorsque :
est dite croissante lorsque :
![]()
![]()
Si la condition
![]()
Parmi les suites non monotones, on distingue les suites oscillantes. Ce sont celles qui varient « en zig-zag », c’est-à-dire que la différence ![]() est de signe alterné (positif ou négatif, selon la parité de
est de signe alterné (positif ou négatif, selon la parité de ![]()
![]() est dite périodique s’il existe un entier
est dite périodique s’il existe un entier ![]() tel que :
tel que :
![]()
![]() est dite majorée si :
est dite majorée si :
![]()
![]()
Une suite simultanément majorée et minorée est dite bornée. Ceci équivaut à :
![]()
Pour la notion de convergence, voir la section 4, plus bas.
Examinons maintenant quelques exemples, en détaillant les calculs …
Exemple 1
La suite définie par :
![]()
Plus généralement, si ![]() est une application croissante, alors la suite définie par la formule explicite :
est une application croissante, alors la suite définie par la formule explicite :
![]()
Dans le cas présent, ![]() est l’application
est l’application
![]()
![]()
Exemple 2
Considérons la suite définie par :
![]()
![]()
Mais méfions-nous des apparences et calculons le quotient ![]() pour le comparer ensuite à 1. Pour tout
pour le comparer ensuite à 1. Pour tout ![]() :
:
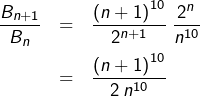
![]()
![]()
L’étude générale des suites dont le terme général est de la forme :
![]()
Exemple 3
La suite définie par :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace C_{n}=\sum_{k=0}^{n}\frac{2^{-k}}{k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5a3d4baa62946ab72249edc1f15323aa_l3.png)
![Rendered by QuickLaTeX.com \[ \forall n\in\mathbb{N},\thinspace S_{n}=\sum_{k=0}^{n}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3d56b0530aed8c1508ba76d5dfd818e2_l3.png)
![Rendered by QuickLaTeX.com \[S_{n+1}-S_{n}=\left(\sum_{k=0}^{n+1}u_{k}\right)-\left(\sum_{k=0}^{n}u_{k}\right)=u_{n+1}\geqslant0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5fb4875c1218f9545bb2f909f17965cb_l3.png)
![Rendered by QuickLaTeX.com \[S_n=\sum_{k=0}^{2n-1}\frac{\left(-1\right)^{k}}{k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-005a0c2d739218dc9b840cee426958ce_l3.png)
![Rendered by QuickLaTeX.com \[S_n=\frac{1}{2}\sum_{k=1}^{n}\frac{1}{k\left(2k-1\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5598cbb5540429082032c997b57b9c21_l3.png)
Exemple 4
Considérons la suite définie par :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace D_{n}=\sum_{k=1}^{n}\frac{1}{n+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6823b05dbc03269606257fb86492e5b7_l3.png)
Pour comprendre ce qui se passe, il sera plus simple d’effectuer un
petit changement d’indice. En posant ![]() on voit que :
on voit que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace D_{n}=\sum_{j=n+1}^{2n}\frac{1}{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c7f16b9dffac6bb436f951aade05ff03_l3.png)
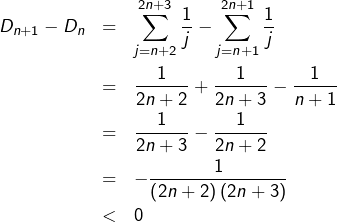
Exemple 5
Considérons la suite définie par :
![]()
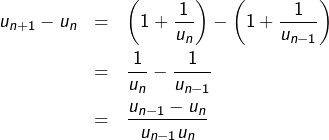
On a donc affaire à une suite oscillante.
L’étude de cette suite sera poursuivie à la section 6
Exemple 6
Considérons la suite définie par :
![]()
La fonction « partie fractionnaire », définie par ![]() pour tout
pour tout ![]() est 1-périodique. La suite de terme général :
est 1-périodique. La suite de terme général :
![]()
![]()
4 – Qu’est ce qu’une suite convergente ?
La notion de convergence pour une suite numérique est moins simple à définir (et à cerner …) que les notions de monotonie, périodicité et autres, vues plus haut.
Il serait incorrect de la définir en disant qu’une suite ![]() converge vers un nombre réel
converge vers un nombre réel ![]() à condition que l’écart
à condition que l’écart ![]() diminue et s’approche indéfiniment de 0. On a en effet envie de considérer que la suite de terme général :
diminue et s’approche indéfiniment de 0. On a en effet envie de considérer que la suite de terme général :
![Rendered by QuickLaTeX.com \[u_{n}=\left\{ \begin{array}{cc}0 & \text{si }n\text{ est pair}\\\\{\displaystyle \frac{1}{n}} & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df52eb9fdfe5512a6f28dcf5abaa0109_l3.png)
La bonne définition remonte au milieu du XIXème siècle. Elle est attribuée à A-L. Cauchy (même s’il y a eu des précurseurs, comme le portugais José Anastácio da Cunha) :
Définition
On dit qu’une suite ![]() de nombres réels converge vers
de nombres réels converge vers ![]() lorsque, pour tout
lorsque, pour tout ![]() il existe un entier
il existe un entier ![]() tel que :
tel que :
![]()
Exemple
Considérons la suite de terme général :
![]()
Pour tout ![]() :
:
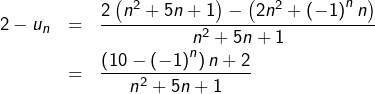
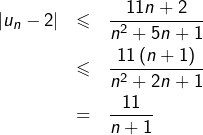
![]()
![]()
On peut prouver les résultats suivants, qui sont fondamentaux :
Théorème 1
Etant données deux suites convergentes ![]() et
et ![]() de limites respectives
de limites respectives ![]() et
et ![]() :
:
- la suite
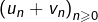 converge vers
converge vers 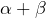
- la suite
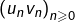 converge vers
converge vers 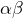
Théorème 2
Etant donnée une suite convergente ![]() de limite
de limite ![]() il existe
il existe ![]() tel que
tel que ![]() dès que
dès que ![]() et la suite
et la suite ![]() converge vers
converge vers ![]()
En combinant le second théorème avec la deuxième partie du premier, on obtient la :
Proposition
Etant données deux suites convergentes ![]() et
et ![]() de limites respectives
de limites respectives ![]() et
et ![]() avec
avec ![]() , la suite
, la suite ![]() est bien définie pour
est bien définie pour ![]() assez grand et converge vers
assez grand et converge vers ![]()
Signalons encore un résultat important :
Lemme de Cesàro
Etant donnée une suite convergente ![]() de limite
de limite ![]() la suite de terme général :
la suite de terme général :
![Rendered by QuickLaTeX.com \[ M_{n}=\frac{1}{n+1}\sum_{k=0}^{n}x_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-45b87f3e681b1ba981d4ae9dd237d3eb_l3.png)
La preuve du lemme de Cesàro constitue une excellente occasion de se frotter à la définition de la convergence, en manipulant des ![]() et des
et des ![]() …
…
On veut montrer que l’écart ![]() peut être rendu arbitrairement petit, pourvu que
peut être rendu arbitrairement petit, pourvu que ![]() soit assez grand.
soit assez grand.
Etant donné ![]() arbitraire, on sait qu’il existe un entier
arbitraire, on sait qu’il existe un entier ![]() tel que :
tel que :
![]()
![Rendered by QuickLaTeX.com \[M_{n}-L=\frac{1}{n+1}\sum_{k=0}^{n}\left(x_{k}-L\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c04a26698a451986a7eac868a9cbdf18_l3.png)
![Rendered by QuickLaTeX.com \[M_{n}-L=\boxed{\frac{1}{n+1}\sum_{k=0}^{N}\left(x_{k}-L\right)}+\frac{1}{n+1}\sum_{k=N+1}^{n}\left(x_{k}-L\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8438e98dcf42b10af2d5bd07d46183e5_l3.png)
Allègeons l’écriture en notant simplement ![]() la quantité encadrée, qui est constante (elle ne dépend pas de
la quantité encadrée, qui est constante (elle ne dépend pas de ![]() :
:
![Rendered by QuickLaTeX.com \[M_{n}-L=\frac{A}{n+1}+\frac{1}{n+1}\sum_{k=N+1}^{n}\left(x_{k}-L\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-afb02e7fa199f80a386f4be4f522e085_l3.png)
![Rendered by QuickLaTeX.com \[\left|M_{n}-L\right|\leqslant\frac{\left|A\right|}{n+1}+\frac{1}{n+1}\sum_{k=N+1}^{n}\left|x_{k}-L\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-47a277bc822aefd183afbe4770d5ad52_l3.png)
![]()
![]()
Pour finir, il existe certainement un entier ![]() tel que :
tel que :
![]()
Remarque : le cas 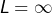
Ce résultat reste valable dans le cas d’une suite qui diverge vers ![]() ou vers
ou vers ![]() Autrement dit, si
Autrement dit, si ![]() alors
alors ![]() et même chose avec
et même chose avec ![]() La démonstration est à peine différente, mais détaillons-la tout de
La démonstration est à peine différente, mais détaillons-la tout de
même, dans le cas où ![]() diverge vers
diverge vers ![]()
Etant donné un réel ![]() arbitraire, il existe un entier
arbitraire, il existe un entier ![]() tel que :
tel que :
![]()
![Rendered by QuickLaTeX.com \[M_{n}=\frac{1}{n+1}\sum_{k=0}^{N}x_{k}+\frac{1}{n+1}\sum_{k=N+1}^{n}x_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d190e373b3a88a08f40d9a7e0ec4f4e_l3.png)
![]()
![]()
Ainsi, pour tout ![]() :
:
![]()
Un article intégralement dédié au lemme de Cesàro et à son histoire est consultable ici.
5 – Convergence monotone
En théorie, la convergence d’une suite peut être établie en se servant de la définition rappelée au début de la section précédente.
Toutefois, dans bon nombre de cas, cette stratégie n’est pas envisageable, pour la simple raison qu’elle exige que la valeur de la limite soit connue à l’avance (voir l’exemple traité à la section 4, ainsi que la preuve du lemme de Cesàro).
Par exemple, il se trouve la suite de terme général :
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}\frac{\cos\left(k\right)}{k^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c96e2f59bc6c452c0b1e79184f53dbbf_l3.png)
Voici un résultat d’usage courant, qui fournit une condition suffisante de convergence :
Théorème de la limite monotone
Toute suite réelle, croissante et majorée ou bien décroissante et minorée, est convergente.
Il est essentiel de bien voir que l’hypothèse ne constitue qu’une condition SUFFISANTE, et pas du tout nécessaire ! Par exemple, la suite de terme général :
![]()
Le théorème de la limite monotone sera admis dans le présent article. Toutefois, le lecteur intéressé pourra consulter ici une preuve. Contentons-nous d’examiner des exemples qui en soulignent l’intérêt.
Exemple 1
Notons, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}\frac{1}{k^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f72f3861d85d23f6f870b66b691b5a2_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\sum_{k=2}^{n}\frac{1}{k^{2}}<\sum_{k=2}^{n}\left(\frac{1}{k-1}-\frac{1}{k}\right)=1-\frac{1}{n}<1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8321888811386355c60fcbe8289a769_l3.png)
![]()
La convergence de la suite ![]() est établie, mais cette méthode nous laisse dans l’ignorance quant à la valeur de sa limite, qu’on peut noter
est établie, mais cette méthode nous laisse dans l’ignorance quant à la valeur de sa limite, qu’on peut noter ![]()
La question du calcul explicite de ![]() constitue le célèbre problème de Bâle, posé en
constitue le célèbre problème de Bâle, posé en ![]() par le mathématicien italien Pietro Mengoli, et résolu environ un siècle plus tard par Leonhard Euler, qui prouva que :
par le mathématicien italien Pietro Mengoli, et résolu environ un siècle plus tard par Leonhard Euler, qui prouva que :
![]()
![]()
Exemple 2
La suite définie par :
![]()
![]()
Comme on le voit d’ailleurs dans l’article en question, on peut prouver (en faisant intervenir les intégrales de Wallis) que :
![]()
6 – Exemples variés d’études de suites
Commençons par deux « incontournables ».
Exemple 1
Donnons-nous un réel ![]() quelconque et un réel
quelconque et un réel ![]() tel que
tel que ![]()
Etudions la suite de terme général :
![]()
![]()
![]()
Notons ![]() En passant à la limite dans l’égalité :
En passant à la limite dans l’égalité :
![]()
Remarque
Ce qui précède inclut le cas particulier de la suite géométrique ![]() (en choisissant
(en choisissant ![]() Bien entendu, une telle suite est (strictement) décroissante, tout court (la mention APCR n’a pas lieu d’être).
Bien entendu, une telle suite est (strictement) décroissante, tout court (la mention APCR n’a pas lieu d’être).
Exemple 2
A présent, fixons un réel ![]() et posons, pour tout
et posons, pour tout ![]() :
:
![]()
![]()
![]()
![]()
On notera que les deux exemples précédents ont été traités essentiellement de la même façon. Passons à l’étude d’une suite définie par itération d’une fonction.
Exemple 3
Reprenons la suite définie par :
![]()
Nous savons qu’elle est oscillante et le théorème de la limite monotone ne peut donc pas lui être appliqué directement.
Une première chose à faire consiste à déterminer sa limite EVENTUELLE.
Supposons un instant que cette suite converge et notons ![]() sa limite. Comme
sa limite. Comme ![]() pour tout
pour tout ![]() alors
alors ![]() et, en particulier :
et, en particulier : ![]() Ceci nous autorise à effectuer un passage à la limite dans l’égalité :
Ceci nous autorise à effectuer un passage à la limite dans l’égalité :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\lambda\in\left\{ \frac{1-\sqrt{5}}{2},\thinspace\frac{1+\sqrt{5}}{2}\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-998cd7ae43ccb3512caa648f046f1f29_l3.png)
![]()

Attention, ceci ne prouve absolument pas que la suite ![]() converge vers cette valeur, mais seulement que SI ELLE CONVERGE, alors c’est nécessairement vers ce nombre (que le lecteur averti aura reconnu : il s’agit du nombre d’or).
converge vers cette valeur, mais seulement que SI ELLE CONVERGE, alors c’est nécessairement vers ce nombre (que le lecteur averti aura reconnu : il s’agit du nombre d’or).
En utilisant le logiciel en ligne live-itération, on peut facilement obtenir le graphique ci-dessous. On y voit les premières étapes de l’itération de la fonction ![]()
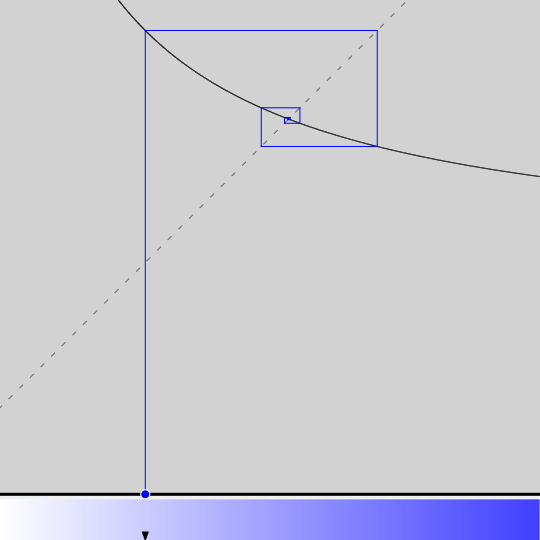
Bien qu’il n’ait évidemment pas valeur de preuve, ce dessin suggère fortement que la suite ![]() converge en oscillant vers une limite plus grande que 1.
converge en oscillant vers une limite plus grande que 1.
Il nous reste à établir rigoureusement cette convergence. Pour cela, l’idée va être de majorer convenablement l’écart ![]() . Etant donné que :
. Etant donné que :
![]()
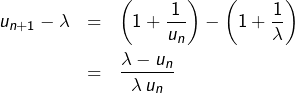
![]()
![]()
Exemple 4
Petit changement d’ambiance … posons, pour tout ![]() :
:
![]()
L’intérêt de ce genre d’exercice tient notamment au fait que l’intégrale n’est pas calculable explicitement (sauf pour ![]() et
et ![]() … exercice pour le lecteur 🙂 ). On doit donc abandonner l’idée de se débarrasser du symbole
… exercice pour le lecteur 🙂 ). On doit donc abandonner l’idée de se débarrasser du symbole ![]()
Avec un peu d’habitude, on pense à faire intervenir ici la majoration suivante :
![]()
On voit ainsi que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[J_{n}\leqslant\int_{0}^{1}t^{n}\thinspace dt=\left[\frac{t^{n+1}}{n+1}\right]_{t=0}^{1}=\frac{1}{n+1} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8a941f3212eeee4ef3d765a93882ffae_l3.png)

Théorème d’encadrement
Soient ![]() sont trois suites réelles. On suppose que
sont trois suites réelles. On suppose que ![]() et, de plus, que les suites
et, de plus, que les suites ![]() et
et ![]() convergent vers une même limite
convergent vers une même limite ![]()
Dans ces conditions, la suite ![]() converge aussi vers
converge aussi vers ![]()
En conclusion, la suite ![]() converge vers 0.
converge vers 0.
Dans les exemples qui précèdent, les suites étudiées étaient convergentes. Terminons avec deux exemples de suites divergentes …
Exemple 5
Posons, pour tout ![]() :
:
![]()
![]()
(![]() )
) ![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N}^{\star},\thinspace H_{2n}-H_{n}\geqslant\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ff43d9dff4f5bdace62fe51cdea9885c_l3.png)
![Rendered by QuickLaTeX.com \[H_{2n}-H_{n}=\sum_{k=n+1}^{2n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-435cf17541d3018088c023746d4d83f1_l3.png)
Si la suite ![]() était majorée, elle convergerait vers une limite
était majorée, elle convergerait vers une limite ![]() En passant à la limite dans l’inégalité
En passant à la limite dans l’inégalité ![]() on obtiendrait :
on obtiendrait :
![]()
Détail (cliquer pour déplier / replier)
On dit d’une suite réelle ![]() qu’elle diverge vers
qu’elle diverge vers ![]() lorsque :
lorsque :
![]()
En effet, soit ![]() une telle suite. Le fait qu’elle ne soit pas majorée se traduit par :
une telle suite. Le fait qu’elle ne soit pas majorée se traduit par :
![]()
![]()
Exemple 6
Fixons un réel ![]() non multiple de
non multiple de ![]() et posons, pour tout
et posons, pour tout ![]() :
:
![]()
On fait donc l’hypothèse que l’une au moins des deux suites converge et l’on cherche une contradiction.
Il sera utile de noter que, pour tout ![]() :
:
![]()
Vu que ![]() la relation
la relation ![]() montre que, pour tout
montre que, pour tout ![]() :
:
![]()
De même, la relation ![]() montre que pour tout
montre que pour tout ![]() :
:
![]()
Bref, la convergence de l’une au moins des deux suites entraîne la convergence des deux.
Notons ![]() les limites respectives de
les limites respectives de ![]() et
et ![]() En passant à la limite dans les relations
En passant à la limite dans les relations ![]() et
et ![]() on voit que :
on voit que :
![]()
![]()
![]()
(![]() )
) ![]()
![]()
(![]() )
) ![]()
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonjour, à propos de la section 6. Convergence d’une suite. L’exemple choisi :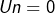 si n pair ,
si n pair , 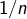 sinon.
sinon.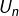 et
et 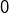 ne décroisse pas de manière uniforme mais plutôt en dents de scie en
ne décroisse pas de manière uniforme mais plutôt en dents de scie en 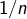 si n impair et 0 sinon. …
si n impair et 0 sinon. … 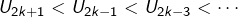 et
et 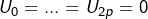 . Le fait que la suite soit oscillante ne me parait pas contredire la définitition de convergence selon Cauchy.
. Le fait que la suite soit oscillante ne me parait pas contredire la définitition de convergence selon Cauchy.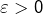 aussi petit soit il, on trouvera toujours un N tel que
aussi petit soit il, on trouvera toujours un N tel que 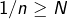 et a fortiori 0 soit plus petit que le Epsilon choisit. N’est ce pas suffisant pour affirmer que
et a fortiori 0 soit plus petit que le Epsilon choisit. N’est ce pas suffisant pour affirmer que 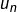 converge vers 0?
converge vers 0?
Je conçois que l’écart entre
Pour n’importe quel
correction, Tous les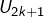 superieurs aux
superieurs aux 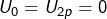
Je pense que vous devez faire référence à la section 4 (et pas 6), où l’on explique que la convergence d’une suite ne saurait être définie en imposant à l’écart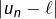 de décroître et de « s’approcher toujours plus de 0 ».
de décroître et de « s’approcher toujours plus de 0 ».
La suite proposée ne vérifie d’ailleurs PAS cette condition et pourtant on a bien envie de la considérer comme une suite convergente. A partir de là, on adopte la définition de la convergence telle que Cauchy l’a formulée.
… et donc, en choisissant N = 1/Epsilon, La suite verifie bien la definition telle que Cauchy l’a formule’e, i.e. elle converge vers 0. Cette conclusion est elle correcte?
En relisant, je pense que le texte veut montrer l’evolution de la notion de suite convergente qui « converge » vers une definition plus precise telle « Cauchy ».
Ah oui, je réalise tout à coup le lapsus ! C’est la réponse du berger à la bergère. Bon, les colles reprennent cette semaine, non plus en MPSI mais en MP2I pour moi. Merci pour vos articles intéressants dans lesquels je puise des idées pour mes exercices.
Bonjour, il manque le cœur et le trèfle pour désigner où sont les deux relations incompatibles. Enfin, elle ne sont pas bien difficiles à localiser. Par contre, il y a beaucoup plus grave : sur la photo, ce ne sont pas des gendarmes mais des policiers !
Bonjour et merci pour votre lecture attentive (et votre œil d’aigle !) : j’ai ajouté en toute fin d’article les deux symboles manquants.
Vous avez raison, j’ai confondu policiers et gendarmes et je m’en excuse. Mais je n’ai pas trouvé meilleure photo …
Et après tout, confondre trèfle et pique, n’est-ce pas tout aussi grave ? 🙂