
1 – En bref …
On a parfois besoin de déterminer le signe d’une expression qui dépend d’une variable réelle ![]() .
.
Notons ![]() une telle expression. Si l’on sait écrire
une telle expression. Si l’on sait écrire ![]() comme le produit de deux expressions plus simples, disons
comme le produit de deux expressions plus simples, disons ![]() et
et ![]() , pour chacune desquelles le signe est connu, il suffit d’appliquer la fameuse règle des signes pour conclure.
, pour chacune desquelles le signe est connu, il suffit d’appliquer la fameuse règle des signes pour conclure.
On présente généralement le résultat dans un tableau qui comporte quatre lignes :
→ une pour ![]()
→ une pour ![]()
→ une pour ![]()
→ une pour ![]()
Bien entendu, ce principe s’applique tout aussi bien pour un plus grand nombre de facteurs ! Par exemple, si ![]() , on ajoutera simplement une ligne au tableau …
, on ajoutera simplement une ligne au tableau …
2 – Un exemple basique
On souhaite déterminer, pour tout ![]() , le signe de :
, le signe de :
![]()
![]()
![]()
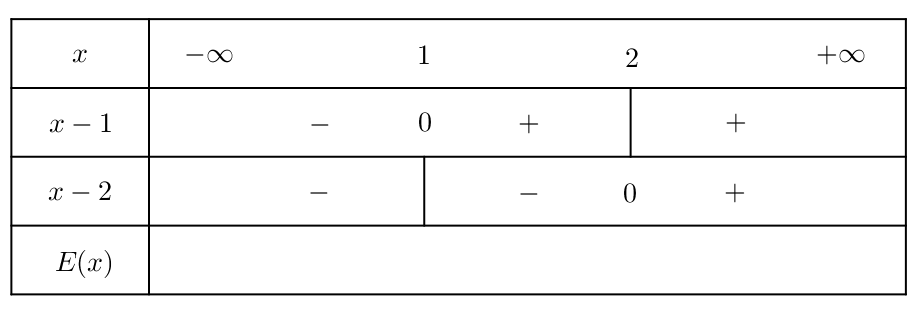
La dernière ligne s’obtient alors, comme on l’a expliqué plus haut, grâce à la règle des signes :
- Si
 , alors
, alors 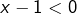 et
et 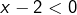 , donc
, donc 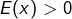
- Si
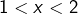 , alors
, alors 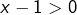 et
et 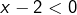 , donc
, donc 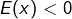
- Si
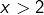 , alors
, alors 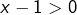 et
et 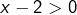 , donc
, donc 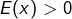
- Si
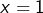 ou
ou 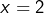 , alors
, alors 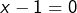 ou
ou 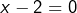 , donc
, donc 
On obtient finalement le tableau de signe :
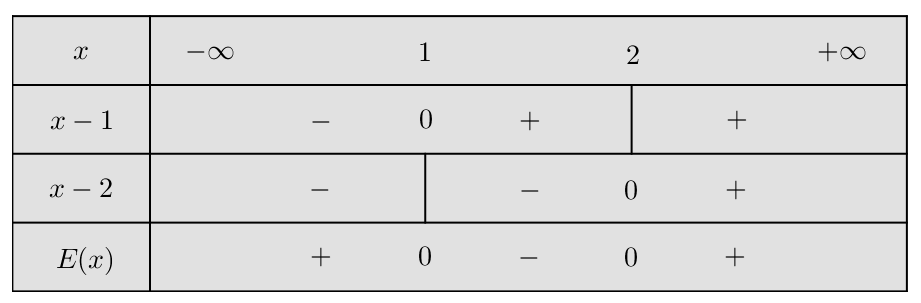
La quantité ![]() est donc :
est donc :
➡ strictement positive pour ![]()
➡ nulle pour ![]()
➡ strictement négative pour ![]()
3 – Un autre exemple, moins basique
On souhaite déterminer, pour tout ![]() , le signe de :
, le signe de :
![]()
L’expression ![]() se présente comme une somme. Comme expliqué au début de ce document, on doit d’abord l’écrire comme un produit : autrement dit, la factoriser.
se présente comme une somme. Comme expliqué au début de ce document, on doit d’abord l’écrire comme un produit : autrement dit, la factoriser.
Pour cela, on peut remarquer que, pour tout ![]() :
:
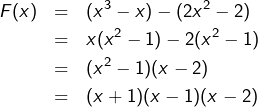
En suivant alors la même démarche que dans l’exemple précédent, on construit le tableau :
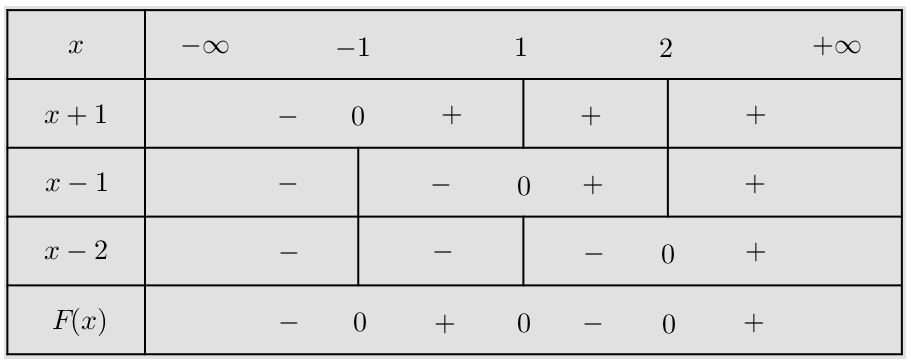
Tout ceci montre que la quantité ![]() est :
est :
➡ strictement positive pour ![]()
➡ nulle pour ![]()
➡ strictement négative pour ![]()
4 – Un dernier exemple, teinté de trigonométrie
On souhaite déterminer le signe de ![]() pour tout
pour tout ![]() .
.
On doit, pour commencer, factoriser ![]() . Pour cela, on utilise la formule de trigonométrie suivante, valable pour tout couple
. Pour cela, on utilise la formule de trigonométrie suivante, valable pour tout couple ![]() de nombres réels :
de nombres réels :
![]()
![]()
Il nous faut maintenant déterminer le signe de chacun des deux facteurs ![]() et
et ![]() .
.
Lorsque ![]() parcourt
parcourt ![]() , on constate que :
, on constate que :
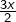 parcourt
parcourt ![Rendered by QuickLaTeX.com \left[0,\frac{3\pi}{2}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6d962714de7814ca269d448fbd8a4775_l3.png)
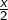 parcourt
parcourt ![Rendered by QuickLaTeX.com \left[0,\frac{\pi}{2}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e9254a292c8c3851d8d369b66f14c9d_l3.png)
Or, on connaît le signe de ![]() sur
sur ![]() et celui de
et celui de ![]() sur
sur ![]() :
:


Il ne reste plus qu’à combiner tout cela, pour obtenir :
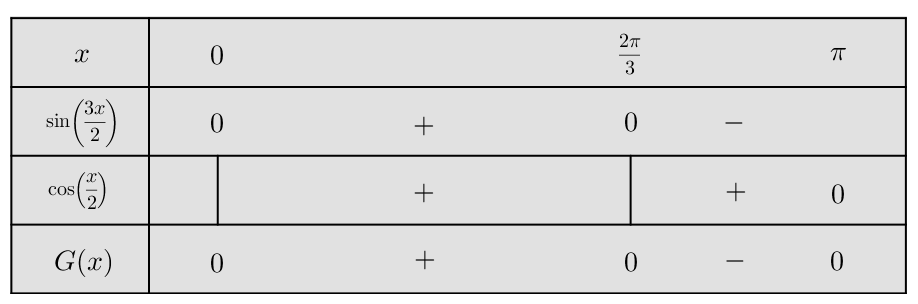
Ainsi, la quantité ![]() est :
est :
➡ strictement positive pour ![]()
➡ nulle pour ![]()
➡ strictement négative pour ![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Yes, ça m’a bien aidé. Merci beaucoup !