Lettre F
FACTORIELLE
Pour chaque entier ![]() on définit sa factorielle, que l’on note
on définit sa factorielle, que l’on note ![]() comme le produit des entiers de 1 à
comme le produit des entiers de 1 à ![]() Par exemple :
Par exemple :
![]()
![]()
La factorielle de ![]() peut s’interpréter comme le nombre de permutations de
peut s’interpréter comme le nombre de permutations de ![]() éléments. Cet article propose une interprétation amusante de la factorielle de
éléments. Cet article propose une interprétation amusante de la factorielle de ![]() (c’est-à-dire du nombre de façons de permuter un jeu de cartes).
(c’est-à-dire du nombre de façons de permuter un jeu de cartes).
Si ![]() sont des entiers tels que
sont des entiers tels que ![]() le coefficient binomial
le coefficient binomial ![]() est donné par :
est donné par :
![]()
Une condition nécessaire et suffisante pour qu’un entier ![]() soit premier est donnée par le théorème de Wilson :
soit premier est donnée par le théorème de Wilson :
![]()
La formule de Stirling donne, lorsqu’on fait tendre ![]() vers
vers ![]() l’estimation asymptotique suivante :
l’estimation asymptotique suivante :
![]()
La fonction Gamma ![]() d’Euler, définie pour tout réel
d’Euler, définie pour tout réel ![]() par :
par :
![]()
Ainsi,
On peut montrer que
![]()
FERMAT (petit théorème de)
Le petit théorème de Fermat ne doit pas être confondu avec le grand théorème de Fermat (ou dernier théorème de Fermat), démontré en 1995 par Andrew Wiles.
petit théorème de Fermat
Etant donné un nombre premier ![]() tout entier naturel
tout entier naturel ![]() vérifie la congruence :
vérifie la congruence :
![]()
On peut prouver ce résultat par récurrence sur ![]() en exploitant la formule du binôme et le fait que :
en exploitant la formule du binôme et le fait que :
![]()
On peut aussi appliquer le théorème de Lagrange au groupe ![]() (groupe de cardinal
(groupe de cardinal ![]() constitué des éléments inversibles du corps
constitué des éléments inversibles du corps ![]()
Ces différents points de vue sont développés dans cet article.
Le petit théorème de Fermat fait l’objet de l’exercice n° 8 de cette fiche.
Une question naturelle est la réciproque : est-ce qu’un entier ![]() vérifiant
vérifiant ![]() pour tout
pour tout ![]() est nécessairement premier ?
est nécessairement premier ?
La réponse est non : il existe des entiers, appelés nombres de Carmichael, qui sont composés (c’est-à-dire non premiers) mais qui vérifient tout de même cette condition. Le plus petit tel entier est 561.
Il est connu (théorème de Alford, Granville et Pomerance – 1994) qu’il existe une infinité de nombres de Carmichael.
Un nombre composé ![]() est dit pseudo-premier en base
est dit pseudo-premier en base ![]() si
si ![]() Les nombres de Carmichael sont donc ceux qui sont pseudo-premiers en toute base. Le fait que les nombres pseudo-premiers simultanément en plusieurs bases soient « suffisamment rares » est à l’origine d’un test de primalité probabiliste, appelé test de Rabin-Miller. Ce test permet d’affirmer – avec certitude – qu’un nombre
Les nombres de Carmichael sont donc ceux qui sont pseudo-premiers en toute base. Le fait que les nombres pseudo-premiers simultanément en plusieurs bases soient « suffisamment rares » est à l’origine d’un test de primalité probabiliste, appelé test de Rabin-Miller. Ce test permet d’affirmer – avec certitude – qu’un nombre ![]() est composé ou bien – avec une très petite probabilité d’erreur – qu’il est premier.
est composé ou bien – avec une très petite probabilité d’erreur – qu’il est premier.
FERMÉ
La notion de partie fermée est présentée ici dans ![]() par souci de simplicité. Son cadre naturel est celui des espaces topologiques.
par souci de simplicité. Son cadre naturel est celui des espaces topologiques.
On dit d’une partie ![]() de
de ![]() que c’est un fermé lorsque son complémentaire est un ouvert; autrement dit lorsque :
que c’est un fermé lorsque son complémentaire est un ouvert; autrement dit lorsque :
![]()
Cette condition équivaut à la suivante (caractérisation séquentielle des fermés) : pour toute suite ![]() à termes dans
à termes dans ![]() si cette suite converge, alors sa limite appartient à
si cette suite converge, alors sa limite appartient à ![]()
L’adjectif « fermé » doit donc être compris comme « fermé pour le passage à la limite » : on ne sort pas de ![]() en prenant la limite d’une suite convergente d’éléments de
en prenant la limite d’une suite convergente d’éléments de ![]()

Attention :
« être un fermé » n’est pas la négation de « être un ouvert » !
Par exemple : ![]() n’est ni un ouvert ni un fermé.
n’est ni un ouvert ni un fermé.
Les parties suivantes de ![]() sont des fermés :
sont des fermés :
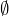

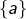
![Rendered by QuickLaTeX.com \left[a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1c9b62f4ffe493505d6566104a9b311_l3.png) pour tout couple
pour tout couple 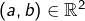 tel que
tel que 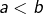
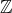
- l’intersection de toute famille de fermés
- l’union d’un famille finie de fermés
- l’image réciproque d’un fermé par une application continue
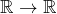
Les parties suivantes de ![]() ne sont pas des fermés :
ne sont pas des fermés :
![Rendered by QuickLaTeX.com \left]a,b\right[,\left[a,b\right[,\left]a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4d4019f2fcc59c5249417065b82670b9_l3.png) pour tout couple
pour tout couple 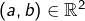 tel que
tel que 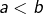
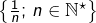
 et
et 
FIBONACCI (suite de)
Définition
La suite d’entiers naturels définie par les relations de récurrence suivantes :
![]()
![]()
Quelques généralités à son sujet sont rassemblées dans cet article.
La suite de Fibonacci vérifie donc une relation de récurrence linéaire du second ordre à coefficients constants. Le polynôme caractéristique associé est ![]() et ses racines sont distinctes; il s’agit de :
et ses racines sont distinctes; il s’agit de :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N},\thinspace F_{n}=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f02c1cfda97a37a484e35bdf783c4f1a_l3.png)
Pour les détails, on pourra consulter l’exemple A de la section 6 de cet article.
On notera qu’il n’est pas du tout évident que le second membre de cette égalité soit un entier naturel … mais c’est pourtant bien le cas !
Parmi les nombreuses propriétés remarquables de la suite ![]() retenons les trois suivantes (la première peut servir de base à un algorithme de calcul rapide des
retenons les trois suivantes (la première peut servir de base à un algorithme de calcul rapide des ![]() :
:
Proposition 1
Pour tout ![]() :
:
![]()
Proposition 2
Pour tout couple ![]() d’entiers naturels :
d’entiers naturels :
![]()
On note ![]() le PGCD des entiers
le PGCD des entiers ![]()
Proposition 3
Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=0}^{n}\binom{n}{k}F_{k}=F_{2n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1433aab9d1cfd355c54a5008ae60084_l3.png)
Les preuves de ces trois propositions sont laissées en pâture au lecteur 🙂 Mais n’hésitez pas – si nécessaire – à demander une indication en passant par le formulaire de contact.
Signalons encore les challenges n° 26 et n° 33 qui portent, l’un comme l’autre, sur la suite de Fibonacci.
FORME LINÉAIRE
Définition
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() on appelle forme linéaire sur
on appelle forme linéaire sur ![]() toute application linéaire de
toute application linéaire de ![]() dans
dans ![]()
Le noyau d’une forme linéaire est :
- l’espace entier (s’il s’agit de la forme linéaire nulle),
- un hyperplan de
 (dans les autres cas).
(dans les autres cas).
Quelques exemples …
Exemple 1
Si ![]() est de dimension finie et si
est de dimension finie et si ![]() est une base de
est une base de ![]() alors l’application
alors l’application ![]() qui à chaque vecteur de
qui à chaque vecteur de ![]() associe sa
associe sa ![]() ème coordonnée dans
ème coordonnée dans ![]() est une forme linéaire, appelée
est une forme linéaire, appelée ![]() ème forme coordonnée relative à
ème forme coordonnée relative à ![]()
La famille ![]() est une base de
est une base de ![]() : c’est la base duale de
: c’est la base duale de ![]()
Exemple 2
Si ![]() alors l’application
alors l’application ![]() est une forme linéaire.
est une forme linéaire.
Son noyau est constitué des polynômes de la forme ![]() avec
avec ![]() arbitraire.
arbitraire.
Exemple 3
Soit ![]() un intervalle non trivial de
un intervalle non trivial de ![]() et
et ![]() l’espace des applications continues et intégrables de
l’espace des applications continues et intégrables de ![]() dans
dans ![]() (la précision « intégrables » étant superflue si
(la précision « intégrables » étant superflue si ![]() est un segment).
est un segment).
L’application ![]() est une forme linéaire.
est une forme linéaire.
Définition
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() on appelle forme linéaire sur
on appelle forme linéaire sur ![]() toute application linéaire de
toute application linéaire de ![]() dans
dans ![]()
Le noyau d’une forme linéaire est :
- l’espace entier (s’il s’agit de la forme linéaire nulle),
- un hyperplan de
 (dans les autres cas).
(dans les autres cas).
Quelques exemples …
Exemple 1
Si ![]() est de dimension finie et si
est de dimension finie et si ![]() est une base de
est une base de ![]() alors l’application
alors l’application ![]() qui à chaque vecteur de
qui à chaque vecteur de ![]() associe sa
associe sa ![]() ème coordonnée dans
ème coordonnée dans ![]() est une forme linéaire, appelée
est une forme linéaire, appelée ![]() ème forme coordonnée relative à
ème forme coordonnée relative à ![]()
La famille ![]() est une base de
est une base de ![]() : c’est la base duale de
: c’est la base duale de ![]()
Exemple 2
Si ![]() alors l’application
alors l’application ![]() est une forme linéaire.
est une forme linéaire.
Son noyau est constitué des polynômes de la forme ![]() avec
avec ![]() arbitraire.
arbitraire.
Exemple 3
Soit ![]() un intervalle non trivial de
un intervalle non trivial de ![]() et
et ![]() l’espace des applications continues et intégrables de
l’espace des applications continues et intégrables de ![]() dans
dans ![]() (la précision « intégrables » étant superflue si
(la précision « intégrables » étant superflue si ![]() est un segment).
est un segment).
L’application ![]() est une forme linéaire.
est une forme linéaire.
Exemple 4
Soit ![]() un espace pré-hilbertien réel et soit
un espace pré-hilbertien réel et soit ![]()
L’application ![]() est une forme linéaire sur
est une forme linéaire sur ![]()
Si de plus ![]() est de dimension finie (espace euclidien), alors toute forme linéaire sur
est de dimension finie (espace euclidien), alors toute forme linéaire sur ![]() est de ce type. C’est le théorème d’isomorphisme canonique entre un espace vectoriel euclidien et son dual (cas particulier du théorème de représentation de Riesz).
est de ce type. C’est le théorème d’isomorphisme canonique entre un espace vectoriel euclidien et son dual (cas particulier du théorème de représentation de Riesz).

