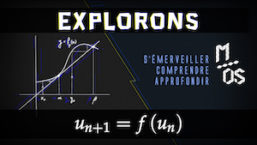
Itération d’une fonction numérique

Description

Etant donné un réel $p\in[0,4]$ , considèrons l’application :

$\boxed{f_p:[0,1]\to[0,1],\,x\mapsto px(1-x)}$

Il est facile de voir que, pour tout $x\in[0,1]$ :

$0\leqslant x(1-x)\leqslant\frac14$

Ceci montre que la définition de $f_p$ tient la route (lorsqu’on applique $f_p$ à un élément de l’intervalle $[0,1]$ , on retombe bien dans cet intervalle).

Etant donné un réel $s\in[0,1]$ , on peut donc définir une suite à termes dans $[0,1]$ en posant :

$\boxed{x_0=s\qquad\text{et}\qquad\forall n\in\mathbb{N},x_{n+1}=f_p(x_n)}$

Et maintenant, on peut se poser tout un tas de questions au sujet de cette suite …

1°) Quel est son comportement ? Est-elle monotone ? Oscillante ?

2°) Quelles sont les couples $(p,s)\in[0,4]\times[0,1]$ pour lesquels elle converge ?

3°) En cas de divergence, que peut-on dire de l’ensemble de ses valeurs d’adhérence ?

4°) Peut-elle être périodique à partir d’un certain rang ?

5°) Pour un $p\text{ donné}$ , est-ce que deux valeurs « voisines » de $s$ donnent lieu à des suites « voisines » ?

Certaines de ces questions sont assez faciles d’accès. D’autres sont d’une difficulté considérable.

Pour celles et ceux qui souhaitent lire un texte mathématique très complet sur ce sujet, je recommande cet article de Daniel Perrin.

Le programme ci-dessous permet, dans une certaine mesure, de visualiser le comportement de la séquence $(x_k)_{0\leqslant k\leqslant n-1}$ .

Vous pouvez faire varier des paramètres et voir, en temps réel, l’impact de ces modifications.

Un mode d’emploi détaillé est donné plus bas, mais si vous préférez consulter une vidéo explicative, la voici :

Le programme Live Iteration !

Mode d’emploi

Ce programme utilise conjointement la souris (ou le trackpad) et le clavier. Il est conçu pour être utilisé sur ordinateur, mais pas sur smartphone ni sur tablette.

En déplaçant le curseur de la souris dans la zone d’entrée (il s’agit de la zone rectangulaire colorée), on fait varier p, n ou s selon le mode actif (indiqué juste au-dessous). Noter que la couleur de la zone d’entrée dépend du mode actif.

On passe d’un mode à l’autre en pressant sur les touche P, N et S respectivement.

– Champs de saisie –

Il est recommandé d’appuyer sur ‘Entrée’ pour valider la saisie (plutôt que ‘Tab’).

Deux champs de saisie permettent de définir les bornes a et b du segment sur lequel la fonction $\mathbf{f}_p$ est définie. En cas de saisie invalide, le programme rectifie de lui-même.

Un troisième champ de saisie autorise la modification de la fonction. Est acceptable toute expression utilisant …

les symboles p et x,
les opérateurs 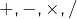$+,-,\times,/$ , ainsi que 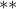$**$ pour l’exponentiation
les parenthèses
les fonctions mathématiques usuelles : sqrt, log, exp, sin, cos, floor, etc …
la constante 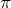$\pi$ , qu’il faut noter PI
la syntaxe condition ? exprVrai : exprFaux (pour définir une fonction par morceaux).

L’expression choisie doit être syntaxiquement correcte (la syntaxe est celle du langage JavaScript) ! En cas de saisie erronée, le programme se rabat sur la dernière fonction valide utilisée antérieurement.

– Principales commandes –

Plusieurs actions sont effectuées en pressant une touche spécifique (ou une combinaison de touches) du clavier …

La touche Alt doit, dans certains environnements, être remplacée par Alt Gr.

Ctrl → ←⭡⭣ : translation du système de coordonnées
+ / – : changement d’échelle (attention : pas les touches du pavé numérique).
Shift → ← : variation fine de s
Alt → ← : variation fine de t si mode SACI activé. Pour savoir ce qu’est ce mode, voir ci-dessous.
Shift + Alt → ← : variation fine de p
Shift ⭡⭣ : variation de n avec un pas de 1.
Shift + déplacement du curseur dans la zone d’entrée : variation du paramètre p, n ou s (selon le mode actif) avec un pas fixé, pour effectuer un ajustement précis.

Et aussi :

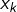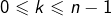A : montre des graduations sur l’axe des abscisses, qui correspondent aux valeurs des $x_k$ pour $0\leqslant k\leqslant n-1$ . Une seconde pression sur cette touche révèle les numéros mais seulement jusqu’à 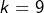$k=9$ . Les graduations sont colorées en gris ou bien alternativement rouges ou bleues, selon la parité de de l’indice 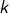$k$ : voir la touche Y plus bas.
B : affichage / masquage de la bissectrice (en pointillés).
D : affichage / masquage du dernier point calculé. Lorsque ce mode est actif, un petit disque apparaît au bout de la ligne polygonale bleue (et aussi de la rouge si le mode SACI est activé.
F : affichage / masquage des points fixes (les points fixes attractifs apparaissent colorés en vert, les super-attractifs en noir, les répulsifs en rouge et les indifférents en blanc).
G : affichage / masquage de la grille.
I : activation / désactivation le calcul des 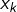$x_k$ pour $0\leqslant k<n$ .
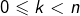M : interrupteur à trois positions, qui met le paramètre n successivement à 2000 (Maximum), à 1 (Minimum), ou à la dernière valeur Mémorisée (obtenue en déplaçant le curseur dans la zone d’entrée ou bien en pressant sur Shift ⭡⭣).
N : passage en mode N. On peut alors faire varier n en déplaçant le curseur dans la zone d’entrée.
P : passage en mode P. On peut alors faire varier n en déplaçant le curseur dans la zone d’entrée.
R : ajustement de l’origine du repère et du facteur d’échelle pour que le carré $[a,b]^2$ soit bien visible.
Shift R : réinitialisation de tous les paramètres aux valeurs par défaut.
S : passage en mode S. On peut alors faire varier s en déplaçant le curseur dans la zone d’entrée.
T : affichage / masquage de la tangente au graphe de 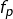$f_p$ , au point de même abscisse que le curseur.
V : activation / désactivation de l’affichage des valeurs d’adhérence (l’activation n’est possible que depuis le mode P et si de plus $n\geqslant 1500$ ).
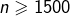X : affichage / masquage des coordonnées du curseur.

Y : coloration simple ou alternée (seulement si l’affichage des 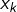$x_k$ est activé : cf. touche A plus haut).
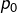Z : activation / désactivation du zoom pour le paramètre p. Cette fonctionnalité n’est disponible que depuis le mode P. Après activation, le domaine de variation du paramètre p n’est plus $[0,4]$ mais $[p_0-(b-a)/10,p_0+(b-a)/10]$ , où $p_0$ désigne la valeur qu’avait 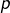$p$ au moment de l’activation.

– Le sous-mode SACI –

En pressant Shift S, on active (ou l’on désactive) le sous-mode Sensibilité Aux Conditions Initiales (« SACI » en abrégé), qui peut coexister en même temps que chacun des modes P, N ou S.

Lorsque ce mode est actif, on voit non pas une mais deux lignes polygonales démarrant respectivement en s (tracée en bleu) et l’autre en t (tracée en rouge), comme indiqué sur la figure ci-dessous :

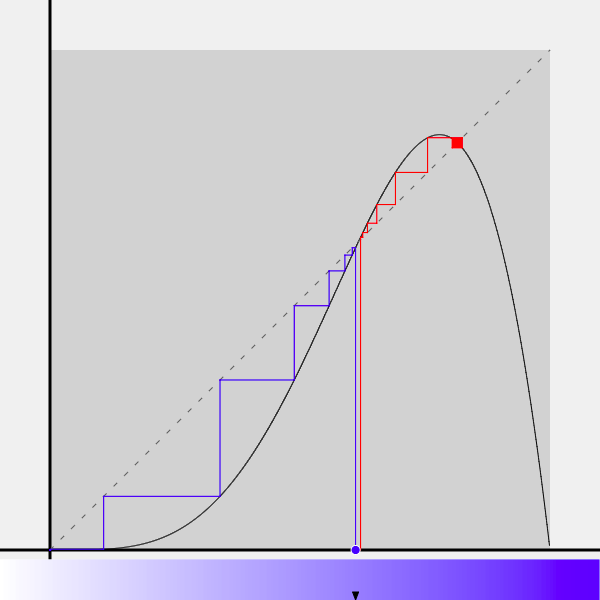
On peut contrôler séparément les valeurs de s et t (à condition que le mode actif soit le mode S) :

pour s, on déplace la souris dans la zone d’entrée.
Et pour t aussi, mais en appuyant en même temps sur la touche Alt (ou Alt Gr dans certains environnements).

Si ce programme vous plaît, ou si vous souhaiter proposer des améliorations,
merci de laisser un commentaire ou bien de passer par le formulaire de contact.