Lettre V

VALEUR ABSOLUE

La valeur absolue d’un nombre réel $A$ est notée $\left|A\right|.$ On peut la définir comme étant :

$\left|A\right|=\left\{ \begin{array}{cc}A & \text{si }A\geqslant0\\0 & \text{sinon}\end{array}\right.$

ou bien, de façon équivalente :

$\left|A\right|=\max\left\{ A,-A\right\}$

L’écart (ou la distance) entre deux nombres réels est mesuré par la valeur absolue de leur différence.

Il est utile de savoir que, pour tout $A\in\mathbb{R}$ :

$\sqrt{A^{2}}=\left|A\right|$

ce qui résulte aussitôt de la définition de la racine carrée d’un réel positif ou nul.

Le résultat suivant est essentiel :

Inégalité triangulaire

Pour tout couple $\left(A,B\right)$ de nombres réels :

avec égalité si, et seulement si, $A$

et $B$

sont de même signe.

Preuve (cliquer pour déplier / replier)

Il revient au même de comparer les carrés. Or d’une part :

$\begin{eqnarray*}\left|A+B\right|^{2} & = & \left(A+B\right)^{2}\\& = & A^{2}+2AB+B^{2}\end{eqnarray*}$

et, d’autre part :

$\begin{eqnarray*}\left(\left|A\right|+\left|B\right|\right)^{2} & = & A^{2}+2\left|A\right|\thinspace\left|B\right|+B^{2}\end{eqnarray*}$

Enfin, l’inégalité triangulaire est une égalité lorsque $AB=\left|AB\right|,$

c’est-à-dire lorsque $AB\geqslant0,$

ce qui signifie précisément que les réels $A$

et $B$

sont de même signe.

On pourra retrouver la preuve ci-dessus (mais pas seulement) dans cette vidéo, qui porte sur l’inégalité triangulaire dans les champs réel et complexe.

VANDERMONDE (formule sommatoire de)

Considérons deux ensembles $A,B$ de cardinaux respectifs $p,q$ et notons $E=A\cup B.$

Etant donné un entier naturel $k$ tel que $k\leqslant p+q,$ combien existe-t-il de parties de $E$ de cardinal $k$ ? Par définition des coefficients binomiaux, la réponse est naturellement :

$\binom{p+q}{k}$

Mais on peut voir les choses différemment.

Une partie de cardinal $k$ de $E$ peut être considérée comme l’union d’une partie $X$ de $A$ et d’une partie $Y$ de $B,$ pourvu que la condition $\text{card}\left(X\right)+\text{card}\left(Y\right)=k$ soit respectée.

En notant $\mathcal{P}_{m}\left(Z\right)$ l’ensemble des parties de $Z$ de cardinal $m$ (où $Z$ désigne un ensemble fini et $m$ un entier naturel), l’affirmation ci-dessus se traduit par :

$\mathcal{P}_{k}\left(E\right)=\bigsqcup_{\left(i,j\right)\in\Omega}\mathcal{P}_{i}\left(A\right)\times\mathcal{P}_{j}\left(B\right)$

l’union disjointe étant indexée par l’ensemble :

$\Omega=\left\{ \left(i,j\right)\in\left\llbracket 0,p\right\rrbracket \times\left\llbracket 0,q\right\rrbracket ;\thinspace i+j=k\right\}$

En passant aux cardinaux, il vient :

( $\star$ ) $\binom{p+q}{k}=\sum_{\left(i,j\right)\in\Omega}\binom{p}{i}\binom{q}{j}$

C’est la formule de Vandermonde, qu’on peut encore écrire :

$\binom{p+q}{k}=\sum_{i=0}^{k}\binom{p}{i}\binom{q}{k-i}$

Mais ATTENTION, dans cette écriture apparaissent des coefficients du type $\binom{\beta}{\alpha}$

avec $\alpha<0$

ou $\alpha>\beta$

: il doivent être considérés comme nuls pour cette formule soit valide. Si l’on s’interdit l’usage de cette convention, on doit écrire plutôt :

( $\star\star$ ) $\boxed{\binom{p+q}{k}=\sum_{i=\max\left\{ 0,k-q\right\} }^{\min\left\{ p,k\right\} }\binom{p}{i}\binom{q}{k-i}}$

Remarque 1

Pour $p=q=k,$ et par symétrie des coefficients binomiaux, la formule $\left(\star\star\right)$ devient :

$\binom{2k}{k}=\sum_{i=0}^{k}\binom{k}{i}^{2}$

Remarque 2

La formule $\left(\star\right)$ se généralise sous la forme :

$\binom{p_{1}+\cdots+p_{r}}{k}=\sum_{\left(i_{1},\cdots,i_{r}\right)\in\Omega}\;\prod_{s=1}^{r}\binom{p_{s}}{i_{s}}$

où l’on a posé :

$\Omega=\left\{ \left(i_{1},\cdots,i_{r}\right)\in\left\llbracket 0,p_{1}\right\rrbracket \times\cdots\times\left\llbracket 0,p_{r}\right\rrbracket ;\thinspace\sum_{s=1}^{r}i_{s}=k\right\}$

Un peu trop abstrait ? Pas de problème, voici un exemple numérique qui pourra aider …

Choisissons $r=3,$ $\left(p_{1},p_{2},p_{3}\right)=\left(2,4,8\right)$ et $k=5.$ Les triplets $\left(i_{1},i_{2},i_{3}\right)$ vérifiant :

$0\leqslant i_{1}\leqslant2,\quad0\leqslant i_{2}\leqslant4,\quad0\leqslant i_{3}\leqslant8\quad\text{et}\quad i_{1}+i_{2}+i_{3}=5$

sont au nombre de 14 :

$\left(2,3,0\right),\quad\left(2,2,1\right),\quad\left(2,1,2\right),\quad\left(2,0,3\right),\quad\left(1,4,0\right),\quad\left(1,3,1\right),\quad\left(1,2,2\right)$

$\left(1,1,3\right),\quad\left(1,0,4\right),\quad\left(0,4,1\right),\quad\left(0,3,2\right),\quad\left(0,2,3\right),\quad\left(0,1,4\right),\quad\left(0,0,5\right)$

On obtient ainsi :

$\begin{eqnarray*}\binom{2+4+8}{5} & = & \binom{2}{2}\binom{4}{3}\binom{8}{0}+\binom{2}{2}\binom{4}{2}\binom{8}{1}+\binom{2}{2}\binom{4}{1}\binom{8}{2}+\\& & \binom{2}{2}\binom{4}{0}\binom{8}{3}+\binom{2}{1}\binom{4}{4}\binom{8}{0}+\binom{2}{1}\binom{4}{3}\binom{8}{1}+\\& & \binom{2}{1}\binom{4}{2}\binom{8}{2}+\binom{2}{1}\binom{4}{1}\binom{8}{3}+\binom{2}{1}\binom{4}{0}\binom{8}{4}+\\& & \binom{2}{0}\binom{4}{4}\binom{8}{1}+\binom{2}{0}\binom{4}{3}\binom{8}{2}+\binom{2}{0}\binom{4}{2}\binom{8}{3}+\\& & \binom{2}{0}\binom{4}{1}\binom{8}{4}+\binom{2}{0}\binom{4}{0}\binom{8}{5}\end{eqnarray*}$

et cette égalité est bien correcte (un petit calcul direct montre que les deux membres valent $2002).$

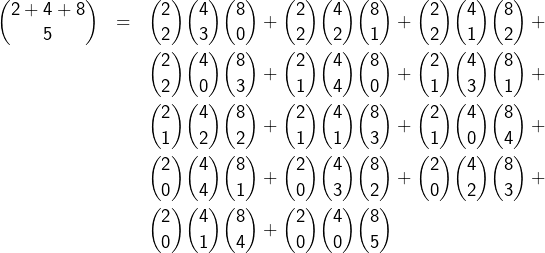
On pourra retrouver ici l’essentiel de cette courte note.

VANDERMONDE (matrice et déterminant de)

« La grande notoriété n’est assurée en Mathématiques qu’aux noms associés à une méthode, à un théorème, à une notation. Peu importe d’ailleurs que l’attribution soit fondée ou non, et le nom de Vandermonde serait ignoré de l’immense majorité des mathématiciens si on ne lui avait attribué ce déterminant que vous connaissez bien, et qui n’est pas de lui ! »

Henri LEBESGUE (conférence donnée à Utrecht, 1937)

Définition

Etant donnée une liste $\left(x_{1},\cdots,x_{n}\right)$ de scalaires, la matrice de Vandermonde associée à cette liste est :

$V\left(x_{1},\cdots,x_{n}\right)=\left[x_{j}^{i-1}\right]_{1\leqslant i,j\leqslant n}$

c’est-à-dire, de manière plus visuelle :

$V\left(x{1},\cdots,x_{n}\right)=\left[\begin{array}{ccccc}1 & 1 & 1 & \cdots & 1\\x_{1} & x_{2} & x_{3} & \cdots & x_{n}\\x_{1}^{2} & x_{2}^{2} & x_{3}^{2} & \cdots & x_{n}^{2}\\\vdots & \vdots & \vdots & & \vdots\\x_{1}^{n-1} & x_{2}^{n-1} & x_{3}^{n-1} & \cdots & x_{n}^{n-1}\end{array}\right]$

On peut éventuellement définir $V\left(x_{1},\cdots,x_{n}\right)$ comme étant la transposée de la matrice ci-desssus, ce qui ne change rien d’essentiel.

La principale propriété de cette matrice est qu’elle est inversible si, et seulement si, les $x_{i}$ sont deux à deux distincts. Ceci résulte de la :

Proposition

Le déterminant de la matrice $V\left(x_{1},\cdots,x_{n}\right)$ est :

$\prod_{1\leqslant i<j\leqslant n}\left(x_{j}-x_{i}\right)$

Preuve (cliquer pour déplier / replier)

Par récurrence sur $n.$ Pour $n=2,$ c’est immédiat puisque :

$\left|\begin{array}{cc}1 & 1\\x_{1} & x_{2}\end{array}\right|=x_{2}-x_{1}$

Supposons la formule établie au rang $n,$

pour un certain $n\geqslant2$

et soient $x_{1},\cdots,x_{n+1}$

des scalaires. Pour factoriser le déterminant de taille $n+1$

$V\left(x_{1},\cdots,x_{n},x_{n+1}\right)=\left|\begin{array}{cccccc}1 & 1 & 1 & \cdots & 1 & 1\\x_{1} & x_{2} & x_{3} & \cdots & x_{n} & x_{n+1}\\x_{1}^{2} & x_{2}^{2} & x_{3}^{2} & \cdots & x_{n}^{2} & x_{n+1}^{2}\\\vdots & \vdots & \vdots & & \vdots & \vdots\\x_{1}^{n-1} & x_{2}^{n-1} & x_{3}^{n-1} & \cdots & x_{n}^{n-1} & x_{n+1}^{n-1}\\x_{1}^{n} & x_{2}^{n} & x_{3}^{n} & \cdots & x_{n}^{n} & x_{n+1}^{n}\end{array}\right|$

on peut retrancher à la ligne $i$

(pour $i=n+1$

à $i=2,$

dans cet ordre), la ligne précédente préalablement multipliée par $x_{1},$

ce qui donne :

$\left|\begin{array}{cccccc}1 & 1 & 1 & \cdots & 1 & 1\\0 & x_{2}-x_{1} & x_{3}-x_{1} & \cdots & x_{n}-x_{1} & x_{n+1}-x_{1}\\0 & x_{2}\left(x_{2}-x_{1}\right) & x_{3}\left(x_{3}-x_{1}\right) & \cdots & x_{n}\left(x_{n}-x_{1}\right) & x_{n+1}\left(x_{n+1}-x_{1}\right)\\\vdots & \vdots & \vdots & & \vdots & \vdots\\0 & x_{2}^{n-2}\left(x_{2}-x_{1}\right) & x_{3}^{n-2}\left(x_{3}-x_{1}\right) & \cdots & x_{n}^{n-2}\left(x_{n}-x_{1}\right) & x_{n+1}^{n-2}\left(x_{n+1}-x_{1}\right)\\0 & x_{2}^{n-1}\left(x_{2}-x_{1}\right) & x_{3}^{n-1}\left(x_{3}-x_{1}\right) & \cdots & x_{n}^{n-1}\left(x_{n}-x_{1}\right) & x_{n+1}^{n-1}\left(x_{n+1}-x_{1}\right)\end{array}\right|$

c’est-à-dire, par multilinéarité par rapport aux colonnes :

$\prod_{j=2}^{n+1}\left(x_{j}-x_{1}\right)\;\left|\begin{array}{cccccc}1 & 1 & 1 & \cdots & 1 & 1\\0 & 1 & 1 & \cdots & 1 & 1\\0 & x_{2} & x_{3} & \cdots & x_{n} & x_{n+1}\\\vdots & \vdots & \vdots & & \vdots & \vdots\\0 & x_{2}^{n-2} & x_{3}^{n-2} & \cdots & x_{n}^{n-2} & x_{n+1}^{n-2}\\0 & x_{2}^{n-1} & x_{3}^{n-1} & \cdots & x_{n}^{n-1} & x_{n+1}^{n-1}\end{array}\right|$

ou encore, en développant par rapport à la première colonne :

$\prod_{j=2}^{n+1}\left(x_{j}-x_{1}\right)\quad V\left(x_{2},\cdots,x_{n+1}\right)$

Grâce à l’hypothèse de récurrence, on conclut que :

$\begin{eqnarray*}V\left(x_{1},\cdots,x_{n},x_{n+1}\right) & = & \prod_{j=2}^{n+1}\left(x_{j}-x_{1}\right)\quad\prod_{2\leqslant i<j\leqslant n+1}\left(x_{j}-x_{i}\right)\\& = & \prod_{1\leqslant i<j\leqslant n+1}\left(x_{j}-x_{i}\right)\end{eqnarray*}$

comme souhaité.

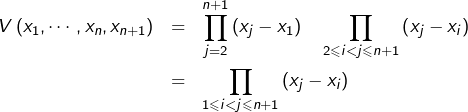
Un exemple d’utilisation est donné dans cette vidéo où l’on prouve, par différentes méthodes, l’indépendance linéaire des fonctions $x\mapsto\cos\left(kx\right)$ pour $1\leqslant k\leqslant n.$

Partager cet article