Exercices sur les suites numériques - 01 - Math-OS

Exercices sur les suites numériques – 01

Auteur/autrice de la publication :René Adad
Post published:26 juillet 2019
Post category:Exercices

Neuf énoncés d’exercices sur les suites numériques (fiche 01).

icone-math-OS-Exos

exercice 1 facile

On définit une suite $u$ par les relations :

$u_{0}=-1$

et

$\forall n\in\mathbb{N},\thinspace u_{n+1}=\frac{u_{n}}{3}-\frac{1}{2}$

Montrer que cette suite converge et préciser sa limite.

exercice 2 facile

Soient $r,s$ deux réels et soit $p\in\left]0,1\right[.$ On définit un couple $\left(a,b\right)$ de suites réelles en posant :

$\left\{\begin{array}{ccc}a_{0} & = & r\\b_{0} & = & s$

et pour tout $n\in\mathbb{N}$ :

$\left\{\begin{array}{ccc}a_{n+1} & = & \left(1-p\right)a_{n}+pb_{n}\\b_{n+1} & = & pa_{n}+\left(1-p\right)b_{n}\end{array}\right.$

Montrer que les suites $a$ et $b$ convergent et préciser leurs limites respectives.

exercice 3 facile

Soit la suite définie par :

$q_{0}=2$

et

$\forall n\in\mathbb{N},\thinspace q_{n+1}=1+\prod_{i=0}^{n}q_{i}$

Trouver une relation de récurrence du premier ordre vérifiée par cette suite.

Calculer 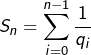$S_{n}=\sum_{i=0}^{n-1}\frac{1}{q_{i}}$ pour $1\leqslant n\leqslant4$ .

Conjecturer une formule générale pour $S_{n}$ puis la démontrer.

Etant donné un réel $s>0,$ on définit une suite $x$ par les relations :

$x_{0}=s$

et

$\forall n\in\mathbb{N},\thinspace x_{n+1}=1+\frac{1}{x_{n}}$

Montrer que cette suite converge vers une limite indépendante de $s.$

On pose, pour tout $n\in\mathbb{N}^{\star}$ :

$H_{n}=\sum_{k=1}^{n}\frac{1}{k}$

Justifier que, pour tout $x>1$ :

$\frac{1}{x-1}+\frac{1}{x}+\frac{1}{x+1}>\frac{3}{x}$

En déduire que la suite $H$ diverge vers l’infini.

Soit $y$ la suite réelle définie par $y_0=0$ et la formule de récurrence :

$\forall n\in\mathbb{N},\thinspace y_{n+1}=\left(n+1\right)y_{n}+1$

Trouver un équivalent de $y_{n}$ lorsque $n\rightarrow\infty.$

Soit $a,b$ deux suites réelles. On suppose $a$ convergente, $b$ bornée et de plus, que :

$\forall n\in\mathbb{N},\thinspace b_{n+1}-b_{n}\leqslant a_{n+1}-a_{n}$

Montrer que $b$ est convergente.

On pose pour tout $n\in\mathbb{N}^{\star}$ :

$P_{n}=\left[\prod_{k=1}^{n}\left(n^{2}+k^{2}\right)\right]^{1/n}$

Montrer qu’il existe deux réels $\lambda,\mu$ (que l’on précisera) tels que :

$P_{n}\sim\lambda\thinspace n^{\mu}\quad\text{lorsque }n\rightarrow\infty$

exercice 9 difficile

Soient $a,b,c$ trois suites réelles vérifiant :

$\left\{ \begin{array}{ccc}{\displaystyle \lim_{n\rightarrow\infty}\left(a_{n}+b_{n}+c_{n}\right)} & = & 0\\\\{\displaystyle \lim_{n\rightarrow\infty}\left(e^{a_{n}}+e^{b_{n}}+e^{c_{n}}\right)} & = & 3\end{array}\right.$

Que peut-on dire ?

Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

Partager cet article

Étiquettes : couple de suites, fonction exponentielle, fonction logarithme, itération, limite monotone, Math-OS, MP*, MPSI, série harmonique, série numérique, somme de Riemann, somme partielle, suite convergente, suite divergente

Laisser un commentaire Annuler la réponse

%d blogueurs aiment cette page :