
Le résultat suivant est bien connu :
Théorème
Soit ![]() un intervalle non trivial de
un intervalle non trivial de ![]()
Si ![]() est dérivable et
est dérivable et ![]() alors
alors ![]() est croissante.
est croissante.
Ce résultat est essentiel à l’étude des variations des fonctions numériques. Il est généralement vu comme conséquence de la formule des accroissements finis :
Preuve (cliquer pour déplier / replier)
Si ![]() est tel que
est tel que ![]() alors il existe
alors il existe ![]() tel que
tel que ![]()
Vue l’hypothèse ![]() on obtient
on obtient ![]() Ainsi,
Ainsi, ![]() est croissante.
est croissante.
L’objet de ce qui suit est de prouver ce théorème, sans recourir à la formule des accroissements finis.
On va suivre le plan de bataille suivant, en deux étapes :
➭ ETAPE 1
Si ![]() sont deux suites à termes dans l’intervalle
sont deux suites à termes dans l’intervalle ![]() vérifiant :
vérifiant :
![]()
![]()
![]()
➭ ETAPE 2
Soit ![]() dérivable et telle que
dérivable et telle que ![]() Alors, en raisonnant par l’absurde et en utilisant l’étape 1, on prouve que
Alors, en raisonnant par l’absurde et en utilisant l’étape 1, on prouve que ![]() est croissante.
est croissante.
Passons aux explications détaillées …
Détail de l’étape 1
Pour tout ![]() , posons :
, posons :
![]()
Posons aussi, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[T(u)=\left\{\begin{array}{cc}\displaystyle{\frac{f(u)-f(\alpha)}{u-\alpha}} & \text{si }u\neq\alpha\\\\f'(\alpha) & \text{sinon}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b4da9032864fd1b1e54a2a1a9f12989d_l3.png)
Alors, pour tout ![]() :
:
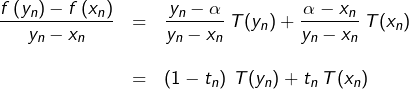
![Rendered by QuickLaTeX.com \[\frac{f\left(y_{n}\right)-f\left(x_{n}\right)}{y_{n}-x_{n}}-f'\left(\alpha\right)=\underbrace{\left(1-t_{n}\right)}_{\textrm{borné}}\,\underbrace{\left[T(y_n)-f'\left(\alpha\right)\right]}_{\rightarrow0}+\underbrace{t_{n}}_{\textrm{borné}}\,\underbrace{\left[T(x_n)-f'\left(\alpha\right)\right]}_{\rightarrow0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3808054355dcef7b8f3c01410b69e7a0_l3.png)
Remarque 1
Si les suites ![]() et
et ![]() convergent vers
convergent vers ![]() du même côté, la conclusion ne persiste pas.
du même côté, la conclusion ne persiste pas.
Pour le voir, on peut considérer l’exemple suivant :
![Rendered by QuickLaTeX.com \[f(x)=\left\{\begin{array}{cc}x^{2}\sin(1/x) & \textrm{si }x\neq0\\\\0 & \textrm{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e03ad4a6689fa52b6915893590626014_l3.png)
![]()
![]()
Remarque 2
Cependant, si ![]() est de classe
est de classe ![]() (c’est-à-dire que
(c’est-à-dire que ![]() est non seulement dérivable mais aussi que
est non seulement dérivable mais aussi que ![]() est continue), alors pour tout couple
est continue), alors pour tout couple ![]() de suites vérifiant les conditions
de suites vérifiant les conditions
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left|\frac{f\left(y_{n}\right)-f\left(x_{n}\right)}{y_{n}-x_{n}}-f'\left(\alpha\right)\right| & = & \left|\frac{1}{y_{n}-x_{n}}\int_{x_{n}}^{y_{n}}\,\left(f'\left(t\right)-f'\left(\alpha\right)\right)\,dt\right|\\& \leqslant & \sup_{t\in\left[x_{n},y_{n}\right]}\left|f'\left(t\right)-f'\left(\alpha\right)\right|\underset{n\rightarrow\infty}{\longrightarrow}0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d79cc73f00237355fd9145571da911da_l3.png)
Détail de l’étape 2
Soit ![]() dérivable et telle que
dérivable et telle que ![]() On suppose l’existence d’un couple
On suppose l’existence d’un couple ![]() tel que
tel que ![]() et
et ![]() et l’on espère bien aboutir à une contradiction !
et l’on espère bien aboutir à une contradiction !
Notons ![]() et
et ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c}{\displaystyle f\left(a\right)-f\left(\frac{a+b}{2}\right)\geqslant\frac{d}{2}}\\\textrm{ou}\\{\displaystyle f\left(\frac{a+b}{2}\right)-f\left(b\right)\geqslant\frac{d}{2}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-13856754ccec52ff588f7d3631208d5a_l3.png)
Posons
On construit ainsi, par récurrence, une suite ![]() de segments, vérifiant :
de segments, vérifiant :
(![]() )
) ![]()
![]()
![Rendered by QuickLaTeX.com \[\bigcap_{n=0}^{\infty}\,\left[x_{n},y_{n}\right]=\left\{ \alpha\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-25d2824e57d7cc68b52a0b78a6e2080e_l3.png)
![]()
![]()
![]()
Mais ceci n’est pas compatible avec l’hypothèse ![]() Nous avons obtenu la contradiction souhaitée. Finalement,
Nous avons obtenu la contradiction souhaitée. Finalement, ![]() est croissante.
est croissante.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonjour Monsieur,
Je vous en prie 😊
Après deux relectures attentives je crois avoir bien compris les arguments en jeu, et je n’ai pas de remarque supplémentaire !
Je vous souhaite un bon dimanche
Merci monsieur pour cette nouvelle réponse !
Je crois que nous parlons de deux points différents 😊
Si vous me le permettez, je retrace mon cheminement en vous posant plusieurs questions, comme cela vous pourrez me dire exactement le moment où je fais probablement fausse route !
– dans la section « Détail de l’étape 2 », juste après « D’après l’étape 1 : », vous utilisez la conclusion (le résultat) de l’étape 1 ?
– si c’est bien le cas, en tout début d’article, après « On va suivre le plan de bataille… », les hypothèses permettant d’appliquer le résultat de l’étape 1 sont annoncées :
lim Xn = lim Yn = alpha et Xn < alpha < Yn pour tout n.
Est-ce bien cela ?
– Ainsi, toujours dans la section « Détail de l’étape 2 », juste après « D’après l’étape 1 », je ne vois pas pourquoi vous ne montrez pas que l’hypothèse « Xn < alpha < Yn pour tout n » est vérifiée avant d’appliquer le résultat 1 ie le quotient tend vers le nombre dérivé ?
Mon point concerne la vérification des hypothèses avant application du résultat de l’étape 1 !
Je suis d’accord avec tout le reste y compris les segments emboîtés 🙂
Bien à vous
Cette fois, je pense avoir compris votre objection et j’ai fait les modifications qui s’imposaient. Vous avez raison, il n’y avait pas adéquation entre les étapes 1 et 2. Cela dit, il s’avère que c’est l’étape 1 que j’ai dû modifier (afin d’autoriser que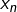 ou que
ou que 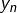 soit égal à
soit égal à 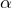 pour certaines valeurs de
pour certaines valeurs de  ) et non l’étape 2. J’ai donc remplacé l’hypothèse
) et non l’étape 2. J’ai donc remplacé l’hypothèse 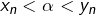 par
par 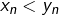 et
et ![Rendered by QuickLaTeX.com \alpha\in[x_n,y_n]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e41efd0801c30eed7b5bc1dff19d331f_l3.png) et j’ai aussi introduit la fonction taux d’accroissement en
et j’ai aussi introduit la fonction taux d’accroissement en 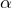 , ou plus exactement son prolongement par continuité, que j’ai noté
, ou plus exactement son prolongement par continuité, que j’ai noté 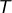 .
.
Vous me direz si ça vous paraît tenir la route à présent. Encore merci pour cet échange fructueux !
Bonsoir Monsieur,
Je vous remercie pour votre réponse.
Le théorème des segments emboîtés et la construction des segments In entraînent que :
– lim Xn = lim Yn = alpha
– et Xn <= alpha <= Yn pour tout n.
Mais les hypothèses énoncées en début d’article permettant d’appliquer l’étape 1 sont un peu plus restrictives :
– lim Xn = lim Yn = alpha ;
– et Xn < alpha < Yn pour tout n (donc X ACPR de limite alpha non autorisée par exemple sauf erreur de ma part).
Mon point d’incompréhension est pourquoi il n’est pas nécessaire de vérifier les hypothèses les plus restrictives avant d’appliquer le résultat de l’état 1 en fin d’article ?
En espérant ne pas être à côté de la plaque 🙂
Bien à vous
Bonjour et merci pour cet échange,
Notre point de désaccord provient sans doute d’un léger écart entre votre énoncé du théorème des segments emboîtés et le mien.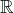 ou, plus généralement, d’un espace métrique complet) dont le diamètre tend vers 0 a pour intersection un singleton.
ou, plus généralement, d’un espace métrique complet) dont le diamètre tend vers 0 a pour intersection un singleton.
Voici l’énoncé sur lequel je m’appuie :
Toute suite décroissante (pour l’inclusion) de fermés non vides (de
Ou bien son corollaire, suffisant ici :
Toute suite décroissante de segments (= intervalles non vides, fermés et bornés de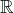 ) dont la longueur tend vers 0 a pour intersection un singleton.
) dont la longueur tend vers 0 a pour intersection un singleton.
Le raisonnement par récurrence signalée dans l’article permet de construire une suite de segments![Rendered by QuickLaTeX.com [x_n,\,y_n]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d98d17520af48cf1b2b12f852e46ddc2_l3.png) vérifiant notamment, pour tout
vérifiant notamment, pour tout 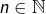 :
:
Ceci permet d’invoquer le théorème précité (ou son corollaire) sans qu’on s’inquiète de savoir si les suites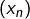 ou
ou 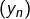 sont stationnaires.
sont stationnaires.
Sommes-nous parvenus à un accord ? 🙂
Bonsoir Monsieur,
Merci pour cet article !
En petites fautes de frappes j’ai relevé au début du détail de l’étape 2 un af(b) qui s’est glissé à la place de f(a)>f(b), et dans l’accolade en-dessous un y qui s’est glissé à la place d’un b.
Lorsque l’étape 1 est appliquée à la suite du théorème des segments emboîtés, comment exclure par exemple le cas où les Xn seraient tous égaux à alpha à partir d’un certain rang (ce qui aurait pour conséquence que la 1ere hypothèse -double inégalité stricte- permettant d’appliquer l’étape 1 ne serait pas vérifiée) ?
Bien à vous
Bonjour et merci pour ce commentaire.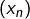 et la suite
et la suite 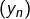 , la construction montre que pour tout
, la construction montre que pour tout 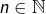 on a
on a 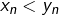 et
et 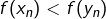 , ce qui permet d’appliquer l’étape 1 à coup sûr. Ceci n’empêche pas, certes, que les
, ce qui permet d’appliquer l’étape 1 à coup sûr. Ceci n’empêche pas, certes, que les 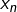 (ou bien les
(ou bien les 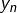 ) soient tous égaux APCR mais ce n’est pas gênant et le théorème des segments emboîtés s’applique quand même. Vous ai-je convaincu ?
) soient tous égaux APCR mais ce n’est pas gênant et le théorème des segments emboîtés s’applique quand même. Vous ai-je convaincu ?
J’ai rectifié les deux coquilles signalées.
Pour ce qui concerne la suite