
Cet article est consacré au résultat classique suivant, connu sous le nom de lemme de Cesàro.
Proposition
Soit ![]() une suite de nombre réels admettant une limite L, finie ou non.
une suite de nombre réels admettant une limite L, finie ou non.
Pour tout ![]() on note
on note ![]() la moyenne des
la moyenne des ![]() premiers termes, c’est-à-dire :
premiers termes, c’est-à-dire :
![Rendered by QuickLaTeX.com \[M_{n}=\frac{1}{n+1}\sum_{k=0}^{n}x_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f4cacb4170154a3750b999c34989e858_l3.png)
Ce résultat est intuitivement simple à comprendre : lorsque ![]() est grand, les termes de la somme sont en majorité très proches de la limite. On s’attend donc à ce que la moyenne soit, elle aussi, proche de cette limite.
est grand, les termes de la somme sont en majorité très proches de la limite. On s’attend donc à ce que la moyenne soit, elle aussi, proche de cette limite.
Une preuve détaillée (et rigoureuse) est consultable ici.
On peut s’étonner de l’appellation « lemme de Cesàro, » dans la mesure ou Cesàro est né en 1859 alors qu’en 1821, Cauchy mentionne déjà ce résultat dans son cours d’Analyse de l’Ecole Royale Polytechnique, sous une forme légèrement différente mais équivalente (qu’on appelle souvent, aujourd’hui, le « lemme de l’escalier »).




Voici l’énoncé en question, sous la plume de Cauchy :

Tâchons d’éclaircir un peu la chronologie des évènements …
1 – Qui a dit quoi avant qui ?
En 1896, Cesàro publie, dans le Bulletin des Sciences Mathématiques, un article intitulé « Sur la multiplication des séries ». Son principal objectif est d’établir que si deux séries numériques convergent, alors leur produit de Cauchy (voir définition de cette notion un peu plus bas) converge en moyenne vers le produit des sommes.
De façon précise, si ![]() et
et ![]() sont deux séries réelles convergentes, de sommes respectives
sont deux séries réelles convergentes, de sommes respectives ![]() et
et ![]() alors en posant pour tout
alors en posant pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[c_{n}=\sum_{k=0}^{n}a_{k}b_{n-k}\qquad\text{et}\qquad X_{n}=\sum_{k=0}^{n}c_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-842c76bd6d1cd8e9546f009efca755b7_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\frac{1}{n+1}\sum_{k=0}^{n}X_{k}=\alpha\beta\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1eb85389d6a627cb9146b408f32bde9e_l3.png)
Lemme de convolution
Si ![]() et
et ![]() sont deux suites réelles convergentes, de limites respectives
sont deux suites réelles convergentes, de limites respectives ![]() et
et ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\frac{1}{n+1}\sum_{k=0}^{n}x_{k}y_{n-k}=\alpha\beta\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2dff0117c1ff87a9743b330d35a4c619_l3.png)
Il s’agit bien d’une généralisation, puisqu’en choisissant les ![]() tous égaux à 1, on retrouve la proposition d’origine.
tous égaux à 1, on retrouve la proposition d’origine.
Ceci explique sans doute (en partie) que la terminologie « lemme de Cesàro » se soit imposée : en effet, on nomme souvent un théorème d’après la personne qui en a fourni l’énoncé le plus général.
Mais il existe une autre raison : la preuve fournie par Cauchy était incorrecte ! En effet, Cauchy s’appuie sur une affirmation préalable, que voici :
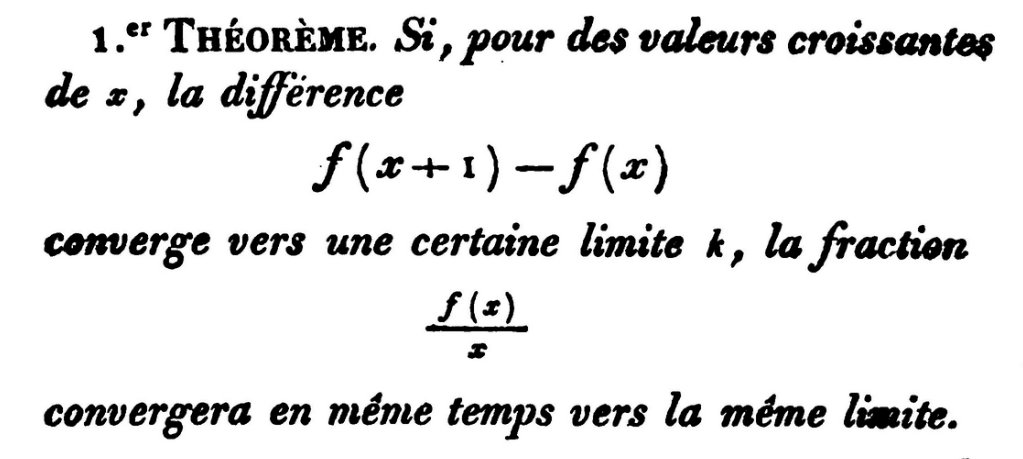
En des termes plus actuels :
Affirmation
Si une application ![]() vérifie la condition
vérifie la condition
(![]() )
) ![]()
(![]() )
) ![]()
Or cette affirmation est FAUSSE ! Il aurait suffit de supposer que ![]() est continue pour arranger les choses, mais Cauchy n’a pas fait cette hypothèse. Certes, on peut toujours imaginer que Cauchy ait sous-entendu cette condition de continuité … mais les faits sont têtus : il n’a rien écrit de tel.
est continue pour arranger les choses, mais Cauchy n’a pas fait cette hypothèse. Certes, on peut toujours imaginer que Cauchy ait sous-entendu cette condition de continuité … mais les faits sont têtus : il n’a rien écrit de tel.
Voici d’ailleurs un contre-exemple. Considérons l’application :
![]()
![]()
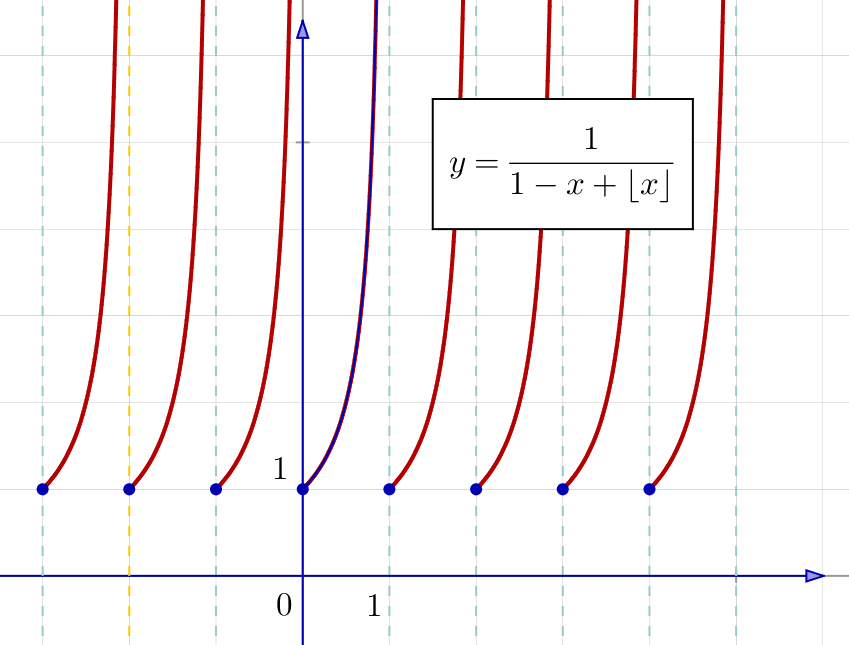
Comme ![]() est
est ![]() périodique, alors
périodique, alors ![]() vérifie trivialement la condition
vérifie trivialement la condition ![]() avec
avec ![]()
Pourtant, lorsque ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\frac{f\left(n-\frac{1}{n}\right)}{n-\frac{1}{n}}=\frac{\varphi\left(1-\frac{1}{n}\right)}{n-\frac{1}{n}}=\frac{n}{n-\frac{1}{n}}\rightarrow1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b9a758664014724cfb0c56170d6228a1_l3.png)
![]()
A présent, examinons en détail les preuves :
- du lemme de convolution,
- du théorème relatif au produit de deux séries convergentes.
2 – Un lemme de convolution
C’est donc Cesàro qui a énoncé en 1896 le résultat suivant :
Lemme
Si ![]() et
et ![]() sont deux suites réelles convergentes, de limites respectives
sont deux suites réelles convergentes, de limites respectives ![]() et
et ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\frac{1}{n+1}\sum_{k=0}^{n}x_{k}y_{n-k}=\alpha\beta\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2dff0117c1ff87a9743b330d35a4c619_l3.png)
Posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[z_{n}=\frac{1}{n+1}\sum_{k=0}^{n}x_{k}y_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6dd78f0520b319c82e5e5a9455b45318_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}z_{n}-\alpha\beta & = & \frac{1}{n+1}\sum_{k=0}^{n}\left(x_{k}y_{n-k}-\alpha\beta\right)\\& = & \frac{1}{n+1}\sum_{k=0}^{n}\left[\left(x_{k}-\alpha\right)y_{n-k}+\alpha\left(y_{n-k}-\beta\right)\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-3f7a8654fc845032358afde804a5ca9b_l3.png)
Ensuite, on sépare en deux sommes puis on ré-indexe la seconde, ce qui donne :
![Rendered by QuickLaTeX.com \[z_{n}-\alpha\beta=\frac{1}{n+1}\sum_{k=0}^{n}\left(x_{k}-\alpha\right)y_{n-k}+\frac{\alpha}{n+1}\sum_{k=0}^{n}\left(y_{k}-\beta\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6370c5b608882162066e9c8e90a948f_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left|z_{n}-\alpha\beta\right|\leqslant\frac{\left|\gamma\right|}{n+1}\sum_{k=0}^{n}\left|x_{k}-\alpha\right|+\frac{\left|\alpha\right|}{n+1}\sum_{k=0}^{n}\left|y_{k}-\beta\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-de217706a79674141a014e21ed9f19ff_l3.png)
![]()
3 – Produit de séries convergentes
Etant données deux séries ![]() et
et ![]() il pourrait sembler naturel de définir leur produit comme étant la série dont le terme général est simplement le produit des termes généraux, c’est-à-dire la série
il pourrait sembler naturel de définir leur produit comme étant la série dont le terme général est simplement le produit des termes généraux, c’est-à-dire la série ![]() .
.
Mais cette définition n’aurait guère d’intérêt. En effet, en cas de convergence des deux séries ![]() et
et ![]() non seulement la série
non seulement la série ![]() peut très bien diverger (voir plus bas), mais même si elle converge, sa somme est en général distincte du produit des sommes.
peut très bien diverger (voir plus bas), mais même si elle converge, sa somme est en général distincte du produit des sommes.
Bref, cette définition naïve du produit ne conduit pas à de bonnes propriétés algébriques.
Voici maintenant le bon point de vue :
Définition
Etant données des séries ![]() et
et ![]() leur produit de Cauchy est la série de terme général :
leur produit de Cauchy est la série de terme général :
![Rendered by QuickLaTeX.com \[c_{n}=\sum_{k=0}^{n}a_{k}b_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddae751d742a69500fc944422afa9b57_l3.png)
Le résultat suivant est fondamental :
Théorème
Si chacune des séries ![]() et
et ![]() est absolument convergente, alors c’est aussi le cas de leur produit de Cauchy et :
est absolument convergente, alors c’est aussi le cas de leur produit de Cauchy et :
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{\infty}c_{n}=\left(\sum_{n=0}^{\infty}a_{n}\right)\left(\sum_{n=0}^{\infty}b_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81f8b91739b63d9ead4f416ba4bc992c_l3.png)
Vous en trouverez une preuve dans cet article sur les séries numériques.
La conclusion est d’ailleurs maintenue sous une hypothèse plus faible, à savoir la convergence absolue de l’une des deux séries et la semi-convergence de l’autre. Ce résultat constitue le théorème de Mertens. Une preuve en est donnée, dans le dernier exercice de cette fiche.
Comme signalé plus haut, il se peut que le produit de Cauchy de deux séries semi-convergentes soit divergent. L’exemple typique est le suivant :
Exemple
On pose ![]() et, pour tout
et, pour tout ![]() :
:
![]()
Mais on constate que pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[c_{n}=\sum_{k=0}^{n}a_{k}b_{n-k}=\left(-1\right)^{n}\:\sum_{k=1}^{n-1}\frac{1}{\sqrt{k\left(n-k\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4eb7168a0bf86d7596ec17548e7f98ff_l3.png)
![]()
![]()
Ces rappels étant faits, il est temps de passer au théorème que Cesàro avait en vue dans son article.
4 – Convergence en moyenne d’un produit de séries convergentes
Théorème (Cesàro, 1896)
Etant données deux séries réelles convergentes ![]() et
et ![]() , de sommes respectives
, de sommes respectives ![]() et
et ![]() , la suite des sommes partielles de leur produit de Cauchy converge, en moyenne de Cesàro, vers
, la suite des sommes partielles de leur produit de Cauchy converge, en moyenne de Cesàro, vers ![]() .
.
Commençons par mettre en place quelques notations. Pour tout ![]() posons :
posons :
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=0}^{n}a_{k},\qquad B_{n}=\sum_{k=0}^{n}b_{k}\qquad X_{n}=\sum_{k=0}^{n}c_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e1580c2a69cccb4b58d41253cd99ec30_l3.png)
![Rendered by QuickLaTeX.com \[c_{k}=\sum_{i=0}^{k}a_{i}b_{k-i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-291309fcf0a62cb7ca9e6f4628f8bf09_l3.png)
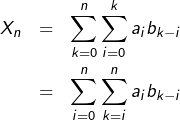
![Rendered by QuickLaTeX.com \[X_{n}=\sum_{i=0}^{n}a_{i}\sum_{k=0}^{n-i}b_{k}=\sum_{i=0}^{n}a_{i}B_{n-i}=\sum_{i=0}^{n}a_{n-i}B_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-005cb82469fc96abc96d5a643d85b62c_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{N}X_{n}=\sum_{n=0}^{N}\sum_{i=0}^{n}a_{n-i}B_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b3d23cec9f7cca16c3fae070cbe18c77_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{N}X_{n}=\sum_{i=0}^{N}\sum_{n=i}^{N}a_{n-i}B_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-268463d0820bae962e1a5efa69c21528_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{N}X_{n}=\sum_{i=0}^{N}A_{n-i}B_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-23d28396af31b88565275b452b5a3ca9_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{N+1}\sum_{n=0}^{N}X_{n}=\frac{1}{N+1}\sum_{i=0}^{N}A_{n-i}B_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ce2132b47ce8d6dc9af1c99c1ac6a68_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{N\rightarrow\infty}\frac{1}{N+1}\sum_{n=0}^{N}X_{n}=\left(\sum_{n=0}^{\infty}a_{n}\right)\left(\sum_{n=0}^{\infty}b_{n}\right)}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-22f1386ae3e74c130d7ebbee64866886_l3.png)
Corollaire
Si ![]() et
et ![]() sont deux séries réelles convergentes dont le produit de Cauchy
sont deux séries réelles convergentes dont le produit de Cauchy ![]() est aussi convergent, alors :
est aussi convergent, alors :
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty c_n=\left(\sum_{n=0}^\infty a_n\right)\,\left(\sum_{n=0}^\infty b_n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-331983e6f6172f7612e7ba355af6d698_l3.png)
En effet, en notant ![]() la suite des sommes partielles du produit de Cauchy, comme cette suite converge vers un certain réel
la suite des sommes partielles du produit de Cauchy, comme cette suite converge vers un certain réel ![]() , alors (lemme de Cesàro) :
, alors (lemme de Cesàro) :
![Rendered by QuickLaTeX.com \[\lim_{n\to\infty}\frac{1}{n+1}\sum_{k=0}^nX_k=\gamma\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5342ba5d0fe95d929374d8617171bfef_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\to\infty}\frac{1}{n+1}\sum_{k=0}^nX_k=\left(\sum_{n=0}^\infty a_n\right)\,\left(\sum_{n=0}^\infty b_n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fff0dc11846ef9320424b55001df07d0_l3.png)


Pour consulter en ligne le cours de Cauchy de 1821, c’est ici.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Ça fonctionne avec le mode horizontal d’un téléphone !
En lisant l’article c’est naturel, car cela permet de lire la partie de l’équation hors champ alors que l’on voit la partie dans le champ. Mais pour les commentaires c’est moins évident d’y penser, car le caractère mathématique que l’on suppose bien présent dans le champ n’est pas visible, mais en effet il apparaît en passant à l’horizontal 😊
Je reviens donc à votre réponse. C’est noté pour votre exemple réel qui achève de montrer que la convergence au sens de Cesàro est plus faible que la convergence au sens usuel. C’est également noté pour la preuve de Cesàro complexe dans le cas infini ie sur une demi droite partant de l’origine. Bien qu’il découle immédiatement du cas infini réel, je trouve dommage que ce dernier cas soit (presque?) jamais mentionné !
Bien à vous
J’ai pensé aussi que cela pouvait provenir du fait que je consulte sur iPhone ! Avec safari / Google / Firefox j’ai le même problème d’affichage dans les commentaires (pas dans l’article!).
A mon retour de vacances je relis l’ensemble de vos réponses sur PC androïd. Merci pour vos réponses 😊
Est-ce que ce problème disparaît en positionnant l’écran de votre iPhone en mode horizontal ?
Dans mon message initial ce n’était pas très beau mais c’était lisible tout en texte 😊
Avec l’ajout de latex certaines parties ne sont désormais plus lisibles !
Mais ce n’était pas mon propos lors de mon deuxième message, je me suis mal exprimé, c’était dans votre réponse que je voulais pointer des parties non visibles, comme tout à la fin par exemple « il suffit d’appliquer … à la suite de terme général… » et le terme général voulu est absent !
Bien à vous
Et maintenant ? J’ai rajouté quelques balises LaTeX à votre précédent message. C’est comme cela qu’il faut procéder pour inclure des formules mathématiques en commentaire.
Les caractères mathématiques ne sont pas passés !
Vous pouvez effacer mon commentaire présent 😊 si vous refaites passer le votre.
Bien à vous
Ok, je comprends. J’ai fait des tests sur d’autres machines et il semble que tout soit OK au niveau de l’affichage. Je pense que le souci doit provenir de votre browser : à l’occasion, pourriez-vous essayer d’en changer et de voir ce que ça donne ?
Bonjour Monsieur,
Merci pour cet article agrémenté de remarques éclairantes (je pense notamment à l’intuition sous-jacente au lemme de Cesàro, ou à l’intérêt de considérer le produit de Cauchy au lieu de la série de terme général égal au produit des termes généraux des deux séries mères).
Si vous le voulez bien j’ai quelques remarques et interrogations :
1) Sauf erreur de ma part, à la fin de l’exemple de la partie 3, la dernière minoration concerne la valeur absolue de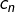 au lieu de
au lieu de 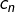 ?
?
2) Le lemme de convolution, tel qu’énoncé dans la partie 1 puis démontré dans la partie 2, est une généralisation du lemme de Cesàro restreint au cas de la limite finie. On pourrait donc parler dans la partie 1 de généralisation partielle lorsque vous montrez qu’il s’agit d’une généralisation ?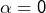 et
et 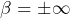 et en évitant également
et en évitant également 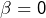 et
et 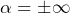 puis en posant les conventions habituelles du type
puis en posant les conventions habituelles du type 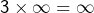 ,
, 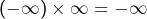 etc …?
etc …?
Cela m’interroge sur l’existence d’une généralisation « totale »? Peut-être en évitant soigneusement les cas
3) Si l’on revient au lemme de Cesàro, le cas réel de la limite finie se généralise sans peine au cas complexe, avec donc toujours une limite finie. Mais à votre connaissance, qu’en est-il du cas
« infini complexe » ? Par exemple dans le cas d’une suite complexe qui « diverge » selon une demi droite en s’éloignant toujours plus de l’origine, sa moyenne de Cesàro aurait-elle un comportement similaire ?
Je comprendrais tout à fait que vous n’ayez pas le temps de répondre, ou que vos réponses soient très brèves !
Bonjour et merci pour ces commentaires pertinents.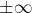 , mais restons simples 🙂 Je me limiterai (jeu de mots …) au cas de deux suites convergentes et il s’agit donc bien d’une généralisation partielle, comme vous l’avez mentionné.
, mais restons simples 🙂 Je me limiterai (jeu de mots …) au cas de deux suites convergentes et il s’agit donc bien d’une généralisation partielle, comme vous l’avez mentionné.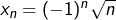 , par exemple (je vous laisse le soin de vérifier que la suite des moyennes converge vers 0). Pour finir, si
, par exemple (je vous laisse le soin de vérifier que la suite des moyennes converge vers 0). Pour finir, si 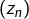 est une suite complexe qui diverge en module vers l’infini mais dont les termes sont tous portés par une demi-droite d’origine 0, alors la suite des moyennes diverge effectivement vers ce qu’on pourrait noter
est une suite complexe qui diverge en module vers l’infini mais dont les termes sont tous portés par une demi-droite d’origine 0, alors la suite des moyennes diverge effectivement vers ce qu’on pourrait noter 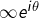 où
où 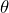 désigne un argument pour cette demi-droite. Pour le démontrer, il suffit d’appliquer le lemme de Cesàro réel à la suite de terme général
désigne un argument pour cette demi-droite. Pour le démontrer, il suffit d’appliquer le lemme de Cesàro réel à la suite de terme général 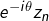 .
.
Pour le 1er point, il s’agissait bien d’une coquille : j’ai donc rajouté la valeur absolue manquante.
Pour le 2nd point, on pourrait effectivement chercher à formuler le lemme de convolution dans le cas ou l’une au moins des deux suites diverge vers
Enfin, pour le 3ème point, dans le cas d’une suite complexe qui diverge en module vers l’infini, la suite des moyennes peut parfaitement converger; cela se voit déjà dans le champ réel en considérant
J’espère avoir répondu à vos questions.
Bien cordialement, R. Adad