Lettre A
ACCROISSEMENT (taux d’)
Soient ![]() un intervalle non trivial,
un intervalle non trivial, ![]() une application de
une application de ![]() dans
dans ![]() et
et ![]() tels que
tels que ![]()
Le taux d’accroissement de ![]() entre
entre ![]() et
et ![]() est le réel :
est le réel :
![]()
Le théorème des accroissements finis dit que si ![]() est dérivable alors il existe
est dérivable alors il existe ![]() tel que :
tel que :
![]()

Pour tout ![]() fixé, on peut définir la « fonction pente » :
fixé, on peut définir la « fonction pente » :
![]()
Par définition, la dérivabilité de ![]() en
en ![]() équivaut à l’existence d’une limite finie pour
équivaut à l’existence d’une limite finie pour ![]() en
en ![]()
Par ailleurs, la convexité de ![]() équivaut à la croissance de
équivaut à la croissance de ![]() pour tout
pour tout ![]()
ADJACENTES (suites)
Deux suites réelles ![]() et
et ![]() sont dites adjacentes lorsque :
sont dites adjacentes lorsque :
- l’une est croissante,
- l’autre est décroissante,
- leur différence tend vers 0.
Proposition
Si les suites réelles ![]() sont adjacentes, alors elles convergent vers une même limite.
sont adjacentes, alors elles convergent vers une même limite.
Pour tout réel ![]() on peut construire un couple
on peut construire un couple ![]() de suites adjacentes, à termes rationnels et dont la limite commune est
de suites adjacentes, à termes rationnels et dont la limite commune est ![]()
Une façon de faire consiste à poser, pour tout ![]() :
:
![]()
Par exemple, pour ![]() les premiers termes de ces suites sont :
les premiers termes de ces suites sont :

On démontre habituellement le théorème des segments emboîtés en considérant la suite ![]() des bornes inférieures, la suite
des bornes inférieures, la suite ![]() des bornes supérieures et en observant qu’elles forment un couple de suites adjacentes.
des bornes supérieures et en observant qu’elles forment un couple de suites adjacentes.
Voici d’autres exemples d’une telle situation :
Exemple 1
Etant donnés ![]() tels que
tels que ![]() on définit deux suites réelles
on définit deux suites réelles ![]() et
et ![]() en posant
en posant ![]()
![]() et :
et :
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N},\thinspace\left\{ \begin{array}{ccc}x_{n+1} & = & \frac{x_{n}+y_{n}}{2}\\\\y_{n+1} & = & \frac{2x_{n}y_{n}}{x_{n}+y_{n}}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7dd92a949a9b451bd9695ea31931fd85_l3.png)
Il est intéressant de constater qu’à chaque étape, ce sont les moyennes arithmétique et harmonique de ![]() qui sont calculées pour obtenir
qui sont calculées pour obtenir ![]() ainsi qu’à la limite, on trouve la moyenne géométrique des deux premiers termes.
ainsi qu’à la limite, on trouve la moyenne géométrique des deux premiers termes.
Voir aussi l’entrée MOYENNES du lexique, pour un exemple construit de façons similaire, mais nettement plus intéressant puisqu’il débouche sur la notion de moyenne arithmético-géométrique.
Exemple 2
Les suites ![]() et
et ![]() respectivement définies par :
respectivement définies par :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace S_{n}=\sum_{k=0}^{n}\frac{1}{k!}\quad\text{et}\quad T_{n}=S_{n}+\frac{1}{n\thinspace n!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d271ae862cc47545f21fcd49617815bf_l3.png)
Une preuve classique de l’irrationalité de ![]() repose d’ailleurs sur l’utilisation de ces deux suites. Voir ici.
repose d’ailleurs sur l’utilisation de ces deux suites. Voir ici.
ADJOINT (endomorphisme)
Etant donnés un espace vectoriel réel ![]() muni d’un produit scalaire et un endomorphisme
muni d’un produit scalaire et un endomorphisme ![]() on s’intéresse aux endomorphismes
on s’intéresse aux endomorphismes ![]() pour lesquels :
pour lesquels :
![]()
Il existe au plus un tel endomorphisme ![]() En effet, si
En effet, si ![]() et
et ![]() conviennent, alors :
conviennent, alors :
![]()
L’existence de ![]() n’est pas assurée en général : voir le dernier exercice de cette fiche.
n’est pas assurée en général : voir le dernier exercice de cette fiche.
En revanche, si ![]() est de dimension finie (ce qu’on suppose désormais), alors il existe un (et donc un seul) tel endomorphisme
est de dimension finie (ce qu’on suppose désormais), alors il existe un (et donc un seul) tel endomorphisme ![]() C’est l’endomorphisme adjoint de
C’est l’endomorphisme adjoint de ![]() habituellement noté
habituellement noté ![]() La proposition suivante rassemble quelques unes des principales propriétés de l’application
La proposition suivante rassemble quelques unes des principales propriétés de l’application ![]() appelée adjonction :
appelée adjonction :
Proposition
L’adjonction est un automorphisme involutif de ![]() ce qui signifie que :
ce qui signifie que :
![]()
![]()
En outre, pour tout couple ![]() :
: ![]()
Si ![]() est une base orthonormale de
est une base orthonormale de ![]() alors les matrices dans
alors les matrices dans ![]() de
de ![]() et de son adjoint sont transposées l’une de l’autre. En conséquence,
et de son adjoint sont transposées l’une de l’autre. En conséquence, ![]() et
et ![]() ont le même rang.
ont le même rang.
Le noyau de ![]() et l’image de
et l’image de ![]() sont supplémentaires orthogonaux.
sont supplémentaires orthogonaux.
La notion d’adjoint permet d’introduire de manière synthétique certaines catégories importantes d’endomorphismes d’un espace euclidien. Notamment :
- les endomorphismes symétriques (ou : auto-adjoints) : ce sont les
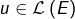 tels que
tels que 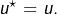
- les endomorphismes antisymétriques : ce sont les
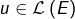 tels que
tels que 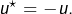
- les automorphismes orthogonaux : ce sont les
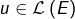 tels que
tels que 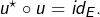
ALEMBERT (règle de d’)
Proposition
Etant donnée une série ![]() à termes strictement positifs, on suppose que la suite
à termes strictement positifs, on suppose que la suite ![]() converge et l’on note :
converge et l’on note :
![]()
- Si
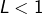 alors la série converge
alors la série converge - Si
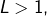 alors la série diverge grossièrement
alors la série diverge grossièrement - Si
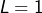 ou si la suite
ou si la suite 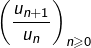 ne possède pas de limite, on ne peut pas conclure.
ne possède pas de limite, on ne peut pas conclure.
Ce résultat est connu sous le nom de règle de d’Alembert … en France, mais dans le reste du monde, on parle plutôt de ratio test. On le démontre en effectuant la comparaison avec une série géométrique.
Le troisième cas est parfois qualifié de « douteux » (puisqu’il n’est pas concluant). Ceci se justifie par le fait que les séries ![]() et
et  sont respectivement divergente et convergente, mais conduisent toutes les deux à
sont respectivement divergente et convergente, mais conduisent toutes les deux à ![]() .
.
Ajoutons qu’il est parfois possible de conclure, même si ![]() : si la suite
: si la suite ![]() est croissante, elle ne peut pas converger vers
est croissante, elle ne peut pas converger vers ![]() et la série est alors grossièrement divergente.
et la série est alors grossièrement divergente.

La règle de d’Alembert ne donne que des conditions suffisantes ! Si ![]() pour tout
pour tout ![]() et si la série
et si la série ![]() converge, il se peut que la suite
converge, il se peut que la suite ![]() ne possède pas de limite. C’est le cas lorsque :
ne possède pas de limite. C’est le cas lorsque :
![Rendered by QuickLaTeX.com \[u_n=\left\{\begin{matrix}\frac{1}{n^2} & \text{si }n\text{ est pair}\\ \\ \frac{1}{n^3} & \text{sinon}\end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f5ee255cb2f7af41e8b63c08a96738f7_l3.png)
Exemples
La série
![Rendered by QuickLaTeX.com \[\boxed{\sum_{n\geqslant1}\frac{n!}{n^{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-de8d38857a0fe81fa3f506a3899ac05d_l3.png)
![]()
Pour la série
![Rendered by QuickLaTeX.com \[\boxed{\sum_{n\geqslant0}\frac{\left(3n\right)!}{27^{n}\left(n!\right)^{3}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-56665f9b9b1032b38140cd2f48a6df09_l3.png)
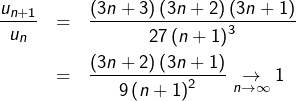
![]()
![Rendered by QuickLaTeX.com \[u_{n}\sim\frac{\left(\frac{3n}{e}\right)^{3n}\left(6\pi n\right)^{1/2}}{27^{n}\left(\frac{n}{e}\right)^{3n}\left(2\pi n\right)^{3/2}}=\frac{K}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b94eac614c832b94d5357f3af6f8c078_l3.png)
ALGÉBRIQUEMENT CLOS (corps)
Un corps ![]() est dit algébriquement clos lorsque tout polynôme
est dit algébriquement clos lorsque tout polynôme ![]() non constant est scindé dans
non constant est scindé dans ![]()
Pour que cette condition soit vérifiée, il suffit que tout polynôme ![]() non constant possède au moins une racine dans
non constant possède au moins une racine dans ![]() (en factorisant par
(en factorisant par ![]() où
où ![]() désigne cette racine, on est ramené à un polynôme de degré moindre et une simple récurrence fait le reste). L’implication réciproque est triviale.
désigne cette racine, on est ramené à un polynôme de degré moindre et une simple récurrence fait le reste). L’implication réciproque est triviale.
L’archétype de corps algébriquement clos est le corps ![]() des nombres complexes. Ce résultat constitue le théorème fondamental de l’algèbre. Il a été conjecturé par d’Alembert (qui en a produit une preuve incorrecte) puis démontré par Gauss, de plusieurs façons.
des nombres complexes. Ce résultat constitue le théorème fondamental de l’algèbre. Il a été conjecturé par d’Alembert (qui en a produit une preuve incorrecte) puis démontré par Gauss, de plusieurs façons.
Proposition
Tout corps algébriquement clos est nécessairement infini.
Preuve (cliquer pour déplier / replier)
Par l’absurde. Supposons que ![]() soit un corps fini algébriquement clos. Notons
soit un corps fini algébriquement clos. Notons ![]() (avec
(avec ![]() ses éléments (parmi lesquels se trouve 1, l’élément neutre multiplicatif de
ses éléments (parmi lesquels se trouve 1, l’élément neutre multiplicatif de ![]() et considérons le polynôme :
et considérons le polynôme :
![Rendered by QuickLaTeX.com \[P=1+\prod_{k=1}^{n}\left(X-a_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b684617c49004a2becbbe627c88569c_l3.png)
On peut montrer que tout corps ![]() possède une clôture algébrique, c’est-à-dire qu’il existe une extension algébrique
possède une clôture algébrique, c’est-à-dire qu’il existe une extension algébrique ![]() de
de ![]() qui soit un corps algébriquement clos. Ce résultat constitue le théorème de Steinitz.
qui soit un corps algébriquement clos. Ce résultat constitue le théorème de Steinitz.

ANTÉCÉDENTS
Considérons deux ensembles ![]() et une application
et une application ![]()
Conventionnellement, ![]() est appelé l’ensemble de départ de
est appelé l’ensemble de départ de ![]() et
et ![]() est appelé l’ensemble d’arrivée de
est appelé l’ensemble d’arrivée de ![]() Chaque élément de
Chaque élément de ![]() de
de ![]() possède une image par
possède une image par ![]() et une seule : il s’agit d’un élément de
et une seule : il s’agit d’un élément de ![]() noté
noté ![]()
A l’inverse, un élément ![]() de
de ![]() n’est pas nécessairement l’image par
n’est pas nécessairement l’image par ![]() d’un élément de
d’un élément de ![]() Il se peut aussi que
Il se peut aussi que ![]() soit l’image de plusieurs éléments de
soit l’image de plusieurs éléments de ![]() (voire, dans certains cas, d’une infinité).
(voire, dans certains cas, d’une infinité).
Les éventuels éléments de ![]() dont
dont ![]() est l’image par
est l’image par ![]() sont les antécédents de
sont les antécédents de ![]() par
par ![]()
Si ![]() est une partie de
est une partie de ![]() alors l’ensemble des antécédents des éléments de
alors l’ensemble des antécédents des éléments de ![]() est l’image réciproque de
est l’image réciproque de ![]() par
par ![]() : il s’agit d’une partie de
: il s’agit d’une partie de ![]() notée
notée ![]() .
.
En particulier, l’ensemble des antécédents de ![]() est noté
est noté ![]() .
.
Exemple
Si ![]() , alors :
, alors :
- -1 ne possède pas d’antécédent par

- 0 en possède un seul (lui-même)
- 4 en possède deux : -2 et 2
Par ailleurs ![]()
A ce sujet, voir cet article.
APCR
On dit qu’une suite réelle ![]() vérifie une propriété
vérifie une propriété ![]() à partir d’un certain rang (APCR en abrégé) lorsqu’il existe un entier naturel
à partir d’un certain rang (APCR en abrégé) lorsqu’il existe un entier naturel ![]() tel que la suite tronquée
tel que la suite tronquée ![]() vérifie
vérifie ![]()
Trivialement, si une suite vérifie ![]() alors elle vérifie
alors elle vérifie ![]() APCR, mais la réciproque est en général fausse.
APCR, mais la réciproque est en général fausse.
Exemple 1
La suite définie par :
![]()
Exemple 2
La suite définie par :
![Rendered by QuickLaTeX.com \[u_{n}=\left\{ \begin{array}{cc}\left(-1\right)^{n} & \text{si }n\leqslant10\\\\\frac{1}{n} & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6346ca9ff76801f067c0198ca81ba69d_l3.png)
Exemple 3
La suite définie par :
![Rendered by QuickLaTeX.com \[u_{n}=\left\{ \begin{array}{cc}n^{2} & \text{si }n\leqslant10\\\\\left(-1\right)^{n} & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ba7bd46afa92bedc81458b6201b9765e_l3.png)
Certains préfère dire « ultimement périodique » pour exprimer la même idée.
Pour certaines propriétés, cette notion ne présente aucun intérêt. Ainsi, une suite bornée APCR est simplement une suite bornée. En effet, s’il existe ![]() et
et ![]() tels que :
tels que :
![]()
![]()
![]()
APPLICATION
Définition
Une application est un triplet ![]() , où
, où ![]() sont des ensembles et
sont des ensembles et ![]() une partie du produit cartésien
une partie du produit cartésien ![]() , tels que :
, tels que :
![]()
![]() est l’ensemble de départ de l’application.
est l’ensemble de départ de l’application.
![]() est l’ensemble d’arrivée de l’application.
est l’ensemble d’arrivée de l’application.
![]() est le graphe de l’application.
est le graphe de l’application.
Pour chaque ![]() , l’unique élément
, l’unique élément ![]() pour lequel
pour lequel ![]() est appelé l’image de
est appelé l’image de ![]() par l’application.
par l’application.
Pour chaque ![]() , les éventuels éléments
, les éventuels éléments ![]() vérifiant
vérifiant ![]() sont appelés les antécédents de
sont appelés les antécédents de ![]() par l’application. Il se peut qu’un élément ne possède :
par l’application. Il se peut qu’un élément ne possède :
- aucun antécédent,
- un seul antécédent,
- plusieurs antécédents (voire une infinité).
Si l’application est notée ![]() , alors l’image de
, alors l’image de ![]() est notée
est notée ![]() .
.
On peut visualiser une application en dessinant des « patates » pour représenter les ensembles de départ et d’arrivée. Chaque couple ![]() appartenant au graphe est alors représenté par une flèche issue de
appartenant au graphe est alors représenté par une flèche issue de ![]() et qui aboutit en
et qui aboutit en ![]() :
:
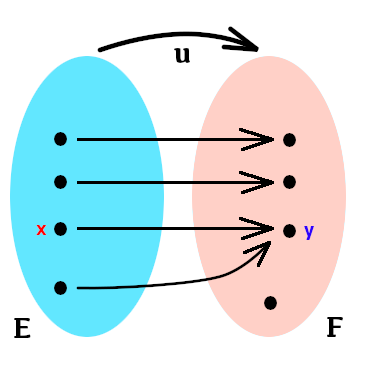
Notation usuelle :
![]()
Définition
Une application est un triplet ![]() , où
, où ![]() sont des ensembles et
sont des ensembles et ![]() une partie du produit cartésien
une partie du produit cartésien ![]() , tels que :
, tels que :
![]()
![]() est l’ensemble de départ de l’application.
est l’ensemble de départ de l’application.
![]() est l’ensemble d’arrivée de l’application.
est l’ensemble d’arrivée de l’application.
![]() est le graphe de l’application.
est le graphe de l’application.
Pour chaque ![]() , l’unique élément
, l’unique élément ![]() pour lequel
pour lequel ![]() est appelé l’image de
est appelé l’image de ![]() par l’application.
par l’application.
Pour chaque ![]() , les éventuels éléments
, les éventuels éléments ![]() vérifiant
vérifiant ![]() sont appelés les antécédents de
sont appelés les antécédents de ![]() par l’application. Il se peut qu’un élément ne possède :
par l’application. Il se peut qu’un élément ne possède :
- aucun antécédent,
- un seul antécédent,
- plusieurs antécédents (voire une infinité).
Si l’application est notée ![]() , alors l’image de
, alors l’image de ![]() est notée
est notée ![]() .
.
On peut visualiser une application en dessinant des « patates » pour représenter les ensembles de départ et d’arrivée. Chaque couple ![]() appartenant au graphe est alors représenté par une flèche issue de
appartenant au graphe est alors représenté par une flèche issue de ![]() et qui aboutit en
et qui aboutit en ![]() :
:

Notation usuelle :
![]()
Exemples
Voici quelques applications …
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\varphi:\mathcal{P}(\mathbb{N})\to[0,2],A\mapsto\sum_{n=0}^\infty\frac{\mathds{1}_A(n)}{2^n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ff6384642400a3f83b726c715bddca4f_l3.png)
Dans ce dernier exemple, ![]() désigne l’ensemble des parties de
désigne l’ensemble des parties de ![]() et
et ![]() désigne la fonction indicatrice de la partie
désigne la fonction indicatrice de la partie ![]() .
.
ASSOCIATIVITÉ
Une opération ![]() sur un ensemble
sur un ensemble ![]() est dite associative lorsque :
est dite associative lorsque :
![]()
Il n’y a alors plus besoin de parenthèses : on peut noter ![]() sans que ceci ne soulève d’ambiguïté.
sans que ceci ne soulève d’ambiguïté.
On peut aussi définir les itérés d’un élément ![]() en posant :
en posant :
![]()
Un ensemble muni d’une opération associative est appelé un semi-groupe. S’il existe en outre un élément neutre ![]() , on parle de monoïde et la définition ci-dessus est prolongée en posant
, on parle de monoïde et la définition ci-dessus est prolongée en posant ![]() .
.
Pour en savoir plus sur l’associativité, on pourra consulter cet article.

