
Dans la première partie de cette introduction à l’étude des séries, sont apparues quelques généralités, ainsi que les résultats de base concernant les séries à termes positifs (SATP).
On a notamment vu que l’étude d’une SATP est facilitée par la croissance de la suite des sommes partielles. Ce simple fait est au cœur du principe de comparaison, qui admet lui-même deux principaux
corollaires :
- la règle de d’Alembert,
- la règle des équivalents.
Lorsque le terme général est de signe constant APCR, l’étude d’une série se ramène aussitôt à celle d’une SATP.
Il n’en va plus de même lorsque le signe du terme général fluctue indéfiniment ou, plus généralement, pour une série à termes complexes.
Cette étude générale est abordée dans le présent texte. Les principaux outils (convergence absolue, théorème des séries alternées, développement asymptotique du terme général et autres …) sont établis de façon détaillée et illustrés d’exemples.
1 – Opérations sur les séries convergentes
Que se passe-t-il si l’on combine entre elles des séries convergentes ?
Avant de répondre à cette question, il convient de préciser ce qu’on entend par « combiner » …
Proposition
Soient ![]() et
et ![]() deux séries complexes convergentes et soit
deux séries complexes convergentes et soit ![]()
Alors la série ![]() est convergente et admet pour somme :
est convergente et admet pour somme :
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{\infty}\left(\lambda a_{n}+b_{n}\right)=\lambda\thinspace\left(\sum_{n=0}^{\infty}a_{n}\right)+\sum_{n=0}^{\infty}b_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-41405c9fcc88729b3efa870d17148f3f_l3.png)
Preuve (cliquer pour déplier / replier)
On revient à la définition de la convergence d’une série, à savoir la convergence de la suite des sommes partielles. Si l’on note, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=0}^{n}a_{k}\qquad\text{et}\qquad B_{n}=\sum_{k=0}^{n}b_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5aa27e7d428c0539307e22c569125e9_l3.png)
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=0}^{n}\left(\lambda\thinspace a_{k}+b_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-22585cda128c95760b88d759db639d81_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\alpha=\sum_{k=0}^{\infty}a_{k}\qquad\text{et}\qquad\beta=\sum_{k=0}^{\infty}b_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c4ab2bd4a8dd7f77d34deb1cac0aa3da_l3.png)
En particulier, la somme de deux séries convergentes converge vers la somme des sommes (!).

Attention, ceci ne fonctionne pas dans l’autre sens… On peut obtenir une série convergente en additionnant deux séries divergentes (il suffit de considérer une série divergente et la série opposée).
Quant à la somme de deux séries de natures contraires (l’une convergente et l’autre divergente), elle est fatalement divergente (sauriez-vous justifier cela ? la réponse est en annexe).
Autre opération importante : le produit deux séries ![]() et
et ![]()
Il ne s’agit pas du produit « naïf », qu’on définirait par ![]() Cette notion n’a d’ailleurs pas beaucoup d’intérêt, car si les trois séries
Cette notion n’a d’ailleurs pas beaucoup d’intérêt, car si les trois séries ![]()
![]() et
et ![]() sont convergentes, on n’a pas de relation spéciale entre leurs sommes. En particulier, l’égalité :
sont convergentes, on n’a pas de relation spéciale entre leurs sommes. En particulier, l’égalité :
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{\infty}a_{n}b_{n}=\left(\sum_{n=0}^{\infty}a_{n}\right)\left(\sum_{n=0}^{\infty}b_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f74036754aaeae5fad321a572d059991_l3.png)
La « bonne » notion est la suivante :
Définition
Le produit de Cauchy des séries complexes ![]() et
et ![]() est la série de terme général :
est la série de terme général :
![Rendered by QuickLaTeX.com \[c_{n}=\sum_{k=0}^{n}a_{k}b_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddae751d742a69500fc944422afa9b57_l3.png)
On en reparle à la section 7 où l’on verra, entre autres, que si les trois séries ![]()
![]() et
et ![]() sont convergentes, alors :
sont convergentes, alors :
![Rendered by QuickLaTeX.com \[\left(\sum_{n=0}^{\infty}a_{n}\right)\left(\sum_{n=0}^{\infty}b_{n}\right)=\sum_{n=0}^{\infty}c_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-262e4acd4c51db4848a1fc69ade333b3_l3.png)
2 – Convergence absolue
Vous préférez visionner une vidéo de 15′ environ sur ce thème ? C’est ici :
Définition
Une série complexe ![]() est dite absolument convergente lorsque la série à termes positifs
est dite absolument convergente lorsque la série à termes positifs ![]() converge.
converge.
Cette définition pourrait sembler un peu vaine sans le résultat spectaculaire suivant :
Théorème
Toute série complexe, absolument convergente, est convergente.
On en trouvera, dans cet article, une preuve détaillée pour les séries à termes réels. Ajoutons le peu qui manque pour le cas d’une série complexe.
Considérons une série ![]() telle que la série
telle que la série ![]() soit convergente. Les inégalités :
soit convergente. Les inégalités :
![]()
Ensuite, la série ![]() apparaît comme combinaison linéaire de deux séries convergentes, puisque pour tout
apparaît comme combinaison linéaire de deux séries convergentes, puisque pour tout ![]() :
:
![]()
Exemple 1
Pour tout ![]() la série :
la série :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant1}\frac{\cos\left(n\right)}{n^{s}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6208ef4831e2c751494f6c2e06f50474_l3.png)
![]()
Exemple 2
La série
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant1}\frac{\left(-1\right)^{n-1}}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1577addab11e5720688d91faf1b85c52_l3.png)
Elle n’est pas absolument convergente, puisqu’en prenant son terme général en valeur absolue, on tombe sur la série harmonique, qui diverge.
Elle est cependant convergente et l’on peut même se payer le luxe d’en calculer la somme.
Pour tout ![]() écrivons la
écrivons la ![]() ème somme partielle sous forme intégrale :
ème somme partielle sous forme intégrale :
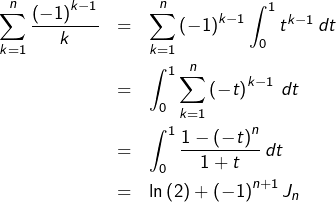
![]()
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}=\ln\left(2\right)}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c4b10d440183b42d43bdfab2169daab_l3.png)
L’exemple qui précède débouche naturellement sur la …
Définition
On qualifie de semi-convergente une série convergente qui n’est pas absolument convergente.
La série harmonique alternée est donc semi-convergente. On verra d’autres exemples à la section suivante, ainsi qu’à la section 5.
3 – Séries alternées
Adoptons la définition suivante (la terminologie varie un peu selon les sources) :
Définition
Une série réelle ![]() est dite alternée si son terme général est de signe alterné, ce qui revient à dire que le signe de
est dite alternée si son terme général est de signe alterné, ce qui revient à dire que le signe de ![]() est indépendant de
est indépendant de ![]()
Pour ce type de séries, le résultat principal est le suivant :
Théorème des séries alternées (TSA)
Si ![]() est une suite réelle qui converge vers 0 en décroissant, alors la série alternée
est une suite réelle qui converge vers 0 en décroissant, alors la série alternée
![]()
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace\left|\sum_{k=n}^{\infty}\left(-1\right)^{k}\alpha_{k}\right|\leqslant\alpha_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-abbe33c773cdd0422a446d2309cc21ab_l3.png)
Preuve (cliquer pour déplier / replier)
On va montrer que la suite ![]() des sommes partielles est convergente, en prouvant que les suites extraites
des sommes partielles est convergente, en prouvant que les suites extraites ![]() et
et ![]() convergent vers une même limite.
convergent vers une même limite.
Posons donc, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ S_{n}=\sum_{k=0}^{n}\left(-1\right)^{k}\alpha_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9234ec251392bf55240d013a0818d84b_l3.png)
![]()
D’autre part :
![]()
![]()
La convergence de la série ![]() est ainsi établie. Notons
est ainsi établie. Notons ![]() sa somme et passons à la majoration du reste.
sa somme et passons à la majoration du reste.
Posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[R_{n}=\sum_{k=n}^{\infty}\left(-1\right)^{k}\alpha_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9e4c0054b4adb48106ba51eb2f6137c0_l3.png)
![]()
![]()
![]()
![]()
Voici maintenant deux exemples d’utilisation du TSA.
Exemple 1
Nous avons rencontré plus haut la série harmonique alternée :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant1}\frac{\left(-1\right)^{n-1}}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1577addab11e5720688d91faf1b85c52_l3.png)
Bien entendu, ceci ne nous donne pas accès au calcul de la somme. En revanche, la majoration du reste nous informe quant à l’erreur commise en remplaçant cette somme par une somme partielle.
Plus précisément :
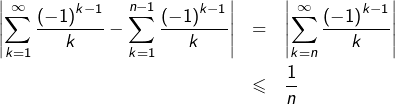
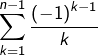 puisse être considéré comme une valeur approchée de
puisse être considéré comme une valeur approchée de Pour atteindre une précision de ![]() il « suffit » donc d’ajouter le premier milliard de termes … ce qui est assez lamentable, en termes d’efficacité !
il « suffit » donc d’ajouter le premier milliard de termes … ce qui est assez lamentable, en termes d’efficacité !
Il existe diverses façons de contourner cet obstacle, en construisant des séries qui convergent très rapidement vers ![]() Mais c’est un autre sujet.
Mais c’est un autre sujet.
Exemple 2
On pose, pour tout ![]() :
:
![]()
On peut toutefois comprendre les choses intuitivement : lorsque ![]() est grand,
est grand, ![]() est voisin de
est voisin de ![]() (si vous en doutez, prenez votre calculette préférée et regardez ce qui se passe pour
(si vous en doutez, prenez votre calculette préférée et regardez ce qui se passe pour ![]() par exemple), de sorte que
par exemple), de sorte que ![]() est « peu différent » de
est « peu différent » de ![]()
Bon. Pas très rigoureux tout ça … et puis, quand bien même on démontrerait que la suite ![]() converge vers 0, cela ne nous apprendrait rien sur la nature de la série
converge vers 0, cela ne nous apprendrait rien sur la nature de la série ![]()
Pour y voir clair, on peut utiliser la technique de l’expression conjuguée pour transformer :
![]()
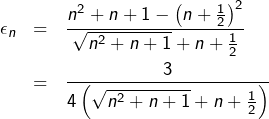
Comme :
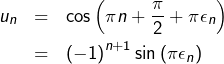
![]()
Ainsi, le TSA s’applique et la série ![]() converge.
converge.
Grâce à la règle des équivalents, on peut ajouter qu’elle est semi-convergente puisque :
![]()
Un exemple (un peu tiré par les cheveux) de série alternée convergente est étudié à l’exercice n° 8 de cette fiche; il s’agit de :
![]()
4 – Développement asymptotique du terme général
Etant donnée une suite ![]() on appelle développement asymptotique à
on appelle développement asymptotique à ![]() termes de cette suite toute écriture de la forme :
termes de cette suite toute écriture de la forme :
![]()
![]()
Il est facile de généraliser cela à un développement asymptotique à ![]() termes. Pour être plus précis, il faudrait définir la notion d’échelle de comparaison, mais restons simples et examinons plutôt deux exemples significatifs qui montrent l’intérêt de cette notion pour l’étude des séries.
termes. Pour être plus précis, il faudrait définir la notion d’échelle de comparaison, mais restons simples et examinons plutôt deux exemples significatifs qui montrent l’intérêt de cette notion pour l’étude des séries.
Exemple 1
On demande la nature de la série de terme général :
![]()
![]()
La bonne idée consiste à développer asymptotiquement le terme général :
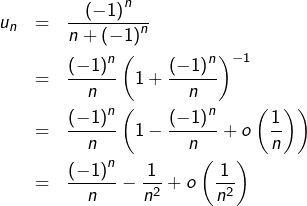
Ce calcul montre que la série ![]() converge puisqu’elle est combinaison linéaire de trois séries convergentes, à savoir :
converge puisqu’elle est combinaison linéaire de trois séries convergentes, à savoir :
- la série harmonique alternée,
- la série de Riemann
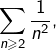
- une série absolument convergente dont le terme général est, en valeur absolue, majoré APCR par
Exemple 2
On demande la nature de la série de terme général :
![]()
![]()
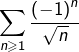 converge (d’après le TSA), cela prouverait que la série
converge (d’après le TSA), cela prouverait que la série 
ATTENTION ! Ce raisonnement est faux !
La règle des équivalents, qui a été étudiée ici, ne s’applique qu’à des séries dont le terme général est de signe constant APCR. On ne peut donc pas l’utiliser dans ce cas.
Vous l’aurez deviné, c’est un développement asymptotique qu’il nous faut :
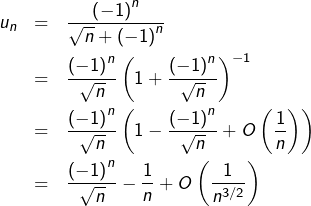
- la série
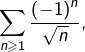 qui converge (d’après le TSA)
qui converge (d’après le TSA) - la série harmonique, qui diverge
- la série « résiduelle », absolument convergente puisque de terme général majoré, en valeur absolue, par
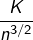 pour un certain
pour un certain 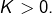
Moralité, la série 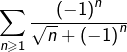 diverge.
diverge.
5 – Règle d’Abel

La transformation d’Abel, que nous allons décrire dans cette section, s’apparente formellement à une intégration par parties … sauf que les intégrales sont remplacées par des sommes ordinaires.
C’est ce qu’on pourrait appeler une IPP « discrète ».
Proposition (transformation d’Abel)
Soient ![]() et
et ![]() Si l’on pose pour tout
Si l’on pose pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[X_{k}=\sum_{j=1}^{k}x_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c64ef189a809b9625b4a1aefab8fb2ff_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\alpha_{k}x_{k}=\alpha_{n}X_{n}+\sum_{k=1}^{n-1}\left(\alpha_{k}-\alpha_{k+1}\right)X_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-031130a994a0ac8d85d2a3363c8988cb_l3.png)
Preuve (cliquer pour déplier / replier)
En remplaçant chaque ![]() par
par ![]() (et en convenant que
(et en convenant que ![]() on obtient :
on obtient :
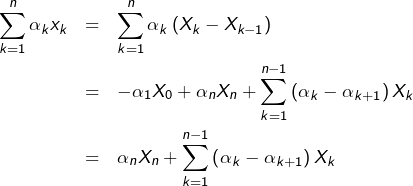
Voici maintenant une condition suffisante de convergence qui vient s’ajouter aux règles déjà connues (et qui permettra parfois de conclure lorsque celles-ci ne s’appliquent pas …).
Règle d’Abel
On suppose que la suite réelle ![]() converge vers
converge vers ![]() en décroissant et que
en décroissant et que ![]() est une suite complexe dont la suite des sommes partielles est bornée.
est une suite complexe dont la suite des sommes partielles est bornée.
Dans ces conditions, la série ![]() est convergente.
est convergente.
Preuve (cliquer pour déplier / replier)
On pose, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[X_{n}=\sum_{k=1}^{n}x_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-90234662befed48363c73ad4a717d637_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\alpha_{k}x_{k}=\alpha_{n}X_{n}+\sum_{k=1}^{n-1}\left(\alpha_{k}-\alpha_{k+1}\right)X_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-031130a994a0ac8d85d2a3363c8988cb_l3.png)
![]()
![]()
Par ailleurs :
![]()
Remarque
Le TSA est un cas particulier de la règle d’Abel ci-dessus puisque, si l’on pose pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[X_n=\sum_{k=0}^n(-1)^k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-84391da66a855a8c3d7129ace33d78a0_l3.png)
Traitons un exemple emblématique d’utilisation de le règle d’Abel.
Proposition
Etant donnés ![]() et
et ![]() la série
la série 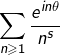 est semi-convergente.
est semi-convergente.
La divergence de la série des modules est évidente, puisque la série de Riemann ![]() diverge.
diverge.
Pour la convergence, on applique la règle d’Abel, en considérant que, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[X_{n}=\sum_{k=1}^{n}e^{ik\theta}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4a0f2f510ebf1e3c12c249afa74b54dc_l3.png)
![]()
![]()
Il résulte de cette proposition que l’ensemble des couples ![]() pour lesquels la série trigonométrique
pour lesquels la série trigonométrique 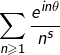 converge est :
converge est :
![]()
Pour un tel couple ![]() les séries
les séries 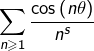 et
et 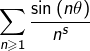 sont donc convergentes. Le sont-elles absolument ou bien sont-elles semi-convergentes ? Cette question est (partiellement) abordée dans l’exercice n° 6 de cette fiche.
sont donc convergentes. Le sont-elles absolument ou bien sont-elles semi-convergentes ? Cette question est (partiellement) abordée dans l’exercice n° 6 de cette fiche.
Concernant la transformation d’Abel, on pourra consulter aussi l’exercice n° 8 de cette fiche.
6 – Séries et intégrales
Dans la première partie de cet exposé, on a étudié la nature des séries de Riemann en effectuant une comparaison série / intégrale.
La proposition suivante décrit cette méthode sous une forme un peu plus générale.
Proposition
Soient ![]() et
et ![]() une application continue, positive et décroissante.
une application continue, positive et décroissante.
La série ![]() et l’intégrale impropre
et l’intégrale impropre ![]() sont de même nature.
sont de même nature.
Preuve (cliquer pour déplier / replier)
Comme ![]() est décroissante, pour tout
est décroissante, pour tout ![]() :
:
![]()
![]()
![Rendered by QuickLaTeX.com \[\int_{N}^{n+1}f\left(t\right)\thinspace dt\leqslant\sum_{k=N}^{n}f\left(k\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aef0632a328a390d2596160b4e54d056_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\sum_{k=N}^{n}f\left(k\right)\leqslant f\left(N\right)+\int_{N}^{n}f\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9962a19020eb61a81826dbcf6c65dd08_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{N}^{n+1}f\left(t\right)\thinspace dt\underset{\star}{\leqslant}\sum_{k=N}^{n}f\left(k\right)\underset{\star\star}{\leqslant}f\left(N\right)+\int_{N}^{n}f\left(t\right)\thinspace dt}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-925edd045b2a8d3b71a4efd09cb4e238_l3.png)
- si la série
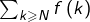 converge, alors pour tout
converge, alors pour tout ![Rendered by QuickLaTeX.com x\in\left]N,+\infty\right[,](https://math-os.com/wp-content/ql-cache/quicklatex.com-a5564877e010545e6c6317b9c9f3cff6_l3.png) on voit avec
on voit avec 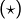 et en tenant compte de la positivité de
et en tenant compte de la positivité de  que :
que :
L’application![Rendered by QuickLaTeX.com \[\int_{N}^{x}f\left(t\right)\thinspace dt\leqslant\int_{N}^{\left\lfloor x\right\rfloor +1}f\left(t\right)\thinspace dt\leqslant\sum_{k=N}^{\left\lfloor x\right\rfloor }f\left(k\right)\leqslant\sum_{k=N}^{\infty}f\left(k\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f6592703855a862cc3ff31e47a91cfe4_l3.png)
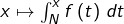 est croissante et majorée, donc possède une limite finie en
est croissante et majorée, donc possède une limite finie en 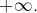 Autrement dit, l’intégrale impropre
Autrement dit, l’intégrale impropre 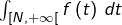 converge.
converge. - si l’intégrale impropre
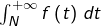 converge, alors d’après
converge, alors d’après  :
:
La suite des sommes partielles est majorée et donc, vue la positivité de son terme général, la série![Rendered by QuickLaTeX.com \[\sum_{k=N}^{n}f\left(k\right)\leqslant f\left(N\right)+\int_{N}^{+\infty}f\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-30ad878deadac87be40aabd2fc8b354c_l3.png)
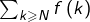 converge.
converge.
Un exemple classique d’utilisation de cette technique (outre les séries de Riemann dont on a déjà parlé) est celui des séries de Bertrand : cette question fait l’objet de l’exercice n° 5 de cette fiche.
Détaillons, en exercice, un exemple similaire :
Exercice
Déterminer les ![]() pour lesquels la série :
pour lesquels la série :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant3}\frac{1}{n\ln\left(n\right)\ln^{\alpha}\left(\ln\left(n\right)\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc3ca8c05025b0e02e96e9ead34d3b73_l3.png)
Une solution est consultable en annexe.
L’idée de comparer une série et une intégrale ne se limite pas au cas où la fonction intégrée est décroissante et positive (même si ce cas est certainement le plus simple). D’une manière générale, on peut espérer découvrir la nature de ![]() en remarquant que, pour tout
en remarquant que, pour tout ![]() :
:
![]()
![]()
Exemple
On demande la nature de la série :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant1}\frac{\cos\left(\pi\sqrt{n}\right)}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9465a1d93e3ebbbe7d5c2e5f92ced0bd_l3.png)
Posons, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[v_{n}=2\thinspace\int_{\sqrt{n}}^{\sqrt{n+1}}\frac{\cos\left(\pi x\right)}{x}\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b17753b6f32c001cd8c9f800703723a1_l3.png)
![Rendered by QuickLaTeX.com \[\frac{\pi}{2}\thinspace v_{n}=\left[\frac{\sin\left(\pi x\right)}{x}\right]_{\sqrt{n}}^{\sqrt{n+1}}+\int_{\sqrt{n}}^{\sqrt{n+1}}\frac{\sin\left(\pi x\right)}{x^{2}}\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0aefe79159e04c4ccf6be5bb391aaf9e_l3.png)
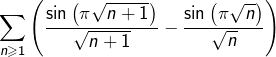 converge (et sa somme est nulle, par sommation télescopique) et, d’autre part, la série
converge (et sa somme est nulle, par sommation télescopique) et, d’autre part, la série 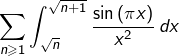 converge absolument, car :
converge absolument, car : ![Rendered by QuickLaTeX.com \[\left|\int_{\sqrt{n}}^{\sqrt{n+1}}\frac{\sin\left(\pi x\right)}{x^{2}}\thinspace dx\right|\leqslant\int_{\sqrt{n}}^{\sqrt{n+1}}\frac{dx}{x^{2}}=\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5a29432877f4d06c7972c0d2db5178b7_l3.png)
![]()
![]()
Finalement, la série ![]() converge aussi, puisque c’est la différence de deux séries convergentes.
converge aussi, puisque c’est la différence de deux séries convergentes.
7 – Produit de Cauchy de deux séries
Le produit de Cauchy de deux séries complexes a été défini à la section 1. Le principal résultat est le suivant :
Théorème (produit de Cauchy de séries ACV)
Si les séries ![]() et
et ![]() sont absolument convergentes, alors leur produit de Cauchy
sont absolument convergentes, alors leur produit de Cauchy ![]() aussi et de plus :
aussi et de plus :
![Rendered by QuickLaTeX.com \[\sum_{n=0}^{\infty}c_{n}=\left(\sum_{n=0}^{\infty}a_{n}\right)\left(\sum_{n=0}^{\infty}b_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81f8b91739b63d9ead4f416ba4bc992c_l3.png)
Preuve (cliquer pour déplier / replier)
Rappelons que, par définition :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace c_{n}=\sum_{k=0}^{n}a_{k}b_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6f22b13483ed6b2a8daea451b0e0192_l3.png)
Posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=0}^{n}a_{k},\qquad B_{n}=\sum_{k=0}^{n}b_{k},\qquad C_{n}=\sum_{k=0}^{n}c_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f6abcd35af65667e3e0a56299273ccb6_l3.png)
![Rendered by QuickLaTeX.com \[\alpha=\sum_{n=0}^{\infty}a_{n},\qquad\beta=\sum_{n=0}^{\infty}b_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ff159be7f3fa36ff32827365e16e7cf_l3.png)
(![]() )
) ![]()
Comme les suites ![]() et
et ![]() convergent respectivement vers
convergent respectivement vers ![]() et
et ![]() leur produit est majoré. La suite
leur produit est majoré. La suite ![]() est ainsi majorée, donc convergente (la suite
est ainsi majorée, donc convergente (la suite ![]() est croissante en raison de la positivité supposée des termes
est croissante en raison de la positivité supposée des termes ![]() et
et ![]() pour tout
pour tout ![]() Notons :
Notons :
![Rendered by QuickLaTeX.com \[\gamma=\sum_{n=0}^{\infty}c_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81270c4fad13b30c494332a033a3fa18_l3.png)
Passons maintenant au cas général (termes complexes). Notons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[c'_{n}=\sum_{k=0}^{n}\left|a_{k}b_{n-k}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f03b073d5e2cbdfe0cb2ab310c905d36_l3.png)
![Rendered by QuickLaTeX.com \[X_{n}=\sum_{k=0}^{n}\left|a_{k}\right|,\qquad Y_{n}=\sum_{k=0}^{n}\left|b_{k}\right|,\qquad Z_{n}=\sum_{k=0}^{n}c'_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cb4d3d7effa58d40ac512d1a03e049c7_l3.png)
![Rendered by QuickLaTeX.com \[\left|A_{n}B_{n}-C_{n}\right|=\left|\sum_{0\leqslant i,j\leqslant n\atop i+j>n}a_ib_j\right|\leqslant\sum_{0\leqslant i,j\leqslant n\atop i+j>n}\left|a_ib_j\right|=X_{n}Y_{n}-Z_{n}\underset{n\to\infty}{\longrightarrow}0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1dc1c2997b3e231d8347961073307bfa_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\sum_{n=0}^\infty c_{n}=\left(\sum_{n=0}^\infty a_{n}\right)\left(\sum_{n=0}^\infty b_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c81916b590c8903da198948d3a7dd990_l3.png)
L’exemple qui suit découle de ce théorème. Il est fondamental :
Proposition
La fonction exponentielle complexe vérifie l’équation fonctionnelle :
![]()
Preuve (cliquer pour déplier / replier)
Rappelons que, par définition :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\forall z\in\mathbb{C},\thinspace\exp\left(z\right)=\sum_{n=0}^{\infty}\frac{z^{n}}{n!}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-439b479fbfd1d6335fd6420ba63e1afc_l3.png)
![]()
![]()
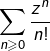 par
par 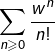 on trouve, d’après le théorème, une série absolument convergente ayant pour somme
on trouve, d’après le théorème, une série absolument convergente ayant pour somme 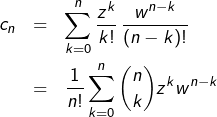
![]()
Etant données deux séries complexes ![]() et
et ![]() voici trois questions qui se posent concernant leur produit de Cauchy
voici trois questions qui se posent concernant leur produit de Cauchy ![]() :
:
- Est-il suffisant que
 et
et 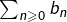 soient convergentes pour que
soient convergentes pour que 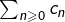 le soit ?
le soit ? - En cas de convergence des trois séries, a-t-on nécessairement :
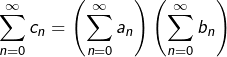 ?
? - Est-il nécessaire que
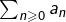 et
et 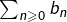 soient absolument convergentes pour que
soient absolument convergentes pour que 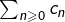 soit convergente ?
soit convergente ?
Les réponses à ces questions sont non, oui et non.
Question 1
Un contre-exemple suffit. Posons, pour tout ![]() :
:
![]()
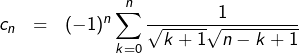
![]()
![]()
Question 2
Il s’agit d’une (jolie) application du lemme de Cesàro. Comme on l’a déjà fait plus haut, notons :
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=0}^{n}a_{k},\qquad B_{n}=\sum_{k=0}^{n}b_{k},\qquad C_{n}=\sum_{k=0}^{n}c_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f6abcd35af65667e3e0a56299273ccb6_l3.png)
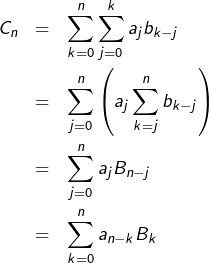
![Rendered by QuickLaTeX.com \begin{eqnarray*}\sum_{n=0}^{N}C_{n} & = & \sum_{n=0}^{N}\left[\sum_{k=0}^{n}a_{n-k}B_{k}\right]\\& = & \sum_{k=0}^{N}\left[\left(\sum_{n=k}^{N}a_{n-k}\right)B_{k}\right]\\& = & \sum_{k=0}^{N}A_{N-k}B_{k}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-996c3f539aa01bbe7052df4ff7efd20f_l3.png)
(![]() )
) ![Rendered by QuickLaTeX.com \[\frac{1}{n+1}\sum_{n=0}^{N}C_{n}=\frac{1}{n+1}\sum_{k=0}^{N}A_{N-k}B_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01a25dbe8b5ae4d25f2cfccb1a285396_l3.png)
Or, on peut montrer que :
Lemme
Si ![]() sont deux suites complexes convergentes, alors la suite de terme général :
sont deux suites complexes convergentes, alors la suite de terme général :
![Rendered by QuickLaTeX.com \[z_{n}=\frac{1}{n+1}\,\sum_{k=0}^{n}\,x_{k}\,y_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddb6782d41a696d1a08351c8d9349162_l3.png)
![]()
Une preuve détaillée de ce lemme est consultable en annexe.
Avec ce résultat en poche, on voit que le membre de droite de ![]() converge vers
converge vers 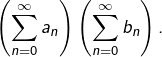
Mais d’après le lemme de Cesàro, le membre de gauche converge vers 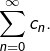 On peut ainsi conclure que :
On peut ainsi conclure que :
![Rendered by QuickLaTeX.com \[{\displaystyle \sum_{n=0}^{\infty}c_{n}}=\left(\sum_{n=0}^{\infty}a_{n}\right)\left(\sum_{n=0}^{\infty}b_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af9d3a7ded009d048e21050440886cb1_l3.png)
Question 3
Cette question débouche sur un résultat connu sous le nom de théorème de Mertens. Selon ce théorème, il suffit que les deux series soient convergentes et que l’une au moins d’entre elles le soit absolument. Une démonstration est proposée à l’exercice n° 9 de cette fiche.
Annexe
1 – Somme de séries de natures contraires
Etant données deux séries de natures contraires (l’une convergente et l’autre divergente), leur somme diverge.
Ceci n’a rien de spécifique aux séries. Considérons deux suites complexes ![]() . Supposons que
. Supposons que ![]() converge et que
converge et que ![]() diverge. Si la suite
diverge. Si la suite ![]() était convergente, alors
était convergente, alors ![]() serait convergente, en tant que différence de deux suites convergentes. Cette contradiction prouve que la suite
serait convergente, en tant que différence de deux suites convergentes. Cette contradiction prouve que la suite ![]() diverge.
diverge.
On peut maintenant appliquer ceci aux suites des sommes partielles pour obtenir le résultat voulu.
2 – Nature d’une série par comparaison à une intégrale
Il s’agissait de discuter, selon la valeur du paramètre réel ![]() , de la nature de la série :
, de la nature de la série :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant3}\frac{1}{n\ln\left(n\right)\ln^{\alpha}\left(\ln\left(n\right)\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc3ca8c05025b0e02e96e9ead34d3b73_l3.png)
Considérons l’application :
![]()
![]()
![]()
Le théorème de comparaison série / intégrale s’applique donc. La série proposée est de même nature que l’intégrale impropre :
![]()
![Rendered by QuickLaTeX.com \[\int_{\ln\left(\ln\left(N\right)\right)}^{+\infty}\frac{dx}{x^{\alpha}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7f395e13318a1d300262dfd8e3261d6a_l3.png)
3 – Un lemme de Cesàro par convolution
Soient ![]() et
et ![]() deux suites complexes convergentes, de limites respectives
deux suites complexes convergentes, de limites respectives ![]() et
et ![]() On définit une suite
On définit une suite ![]() en posant, pour tout
en posant, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[z_{n}=\frac{1}{n+1}\,\sum_{k=0}^{n}\,x_{k}\,y_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddb6782d41a696d1a08351c8d9349162_l3.png)
On peut déjà deviner quelle pourrait être cette limite, en examinant le cas particulier où l’une des deux suites est constante. En effet, si ![]() pour tout
pour tout ![]() alors le lemme de Cesàro montre que
alors le lemme de Cesàro montre que ![]()
Cela dit, revenons au cas général. On constate que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*}z_{n}-ab & = & \frac{1}{n+1}\,\sum_{k=0}^{n}\,\left[\left(x_{k}-a\right)y_{n-k}+a\left(y_{n-k}-b\right)\right]\\& = & \frac{1}{n+1}\,\sum_{k=0}^{n}\,\left(x_{k}-a\right)y_{n-k}+\frac{a}{n+1}\,\sum_{j=0}^{n}\,\left(y_{j}-b\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-e99ed806c3b57488ce867c4249c69538_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left|z_{n}-ab\right|\leqslant\frac{M}{n+1}\,\sum_{k=0}^{n}\,\left|x_{k}-a\right|+\frac{\left|a\right|}{n+1}\,\sum_{k=0}^{n}\,\left|y_{k}-b\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-efa301e17d5d9c807755b3434c60c29e_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\frac{1}{n+1}\,\sum_{k=0}^{n}\,\left|x_{k}-a\right|=\lim_{n\rightarrow\infty}\frac{1}{n+1}\,\sum_{k=0}^{n}\,\left|y_{k}-b\right|=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-022574f5c9675693074862d8f47fec58_l3.png)
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.


Ce riche article nécessitera pour ma part au moins une deuxième lecture !
Il est intéressant de lire et comprendre que le théorème des séries alternées est un cas particulier de la règle d’Abel (la règle d’Abel est (était?) hors programme MP et donc non enseignée dans une MP « modeste », du moins dans les années 2000).
Pour les moins affûtés -comme moi-, dans le deuxième exemple de la partie 3, on peut écrire :
rac(n^2 + n + 1) = rac((n + 1/2)^2 + 3/4) qui est proche de rac((n + 1/2)^2 ) ie n + 1/2 pour n grand, car le terme 3/4 devient négligeable devant les autres quantités qui croissent vers + l’infini.
Bien à vous.