
Cet article suppose connue la notion de suite réelle convergente (ou, plus généralement, de suite complexe convergente).
Si nécessaire, on pourra consulter les sections 4 et 5 de l’article Comment étudier une suite ? ainsi que la section 1 de l’article Initiation aux suites de Cauchy.
Une certaine familiarité avec la notation ![]() est également nécessaire. L’article Manipulation de sommes à l’aide du symbole Σ doit permettre d’y remédier, en cas de besoin.
est également nécessaire. L’article Manipulation de sommes à l’aide du symbole Σ doit permettre d’y remédier, en cas de besoin.
Lorsque vos connaissances sur le thème des séries numériques commenceront à être en place, des exercices corrigés vous attendent :
Fiche d’exercices n° 1 ; Fiche d’exercices n° 2 ; Fiche d’exercices n° 3
1 – Préliminaires & Notations
A toute suite complexe ![]() on peut associer la suite
on peut associer la suite ![]() définie par :
définie par :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{S_{n}=\sum_{k=0}^{n}u_{k}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0eb5d214a038923712476fe6399bf9bb_l3.png)
Deux questions se posent :
- La suite
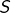 est-elle convergente ?
est-elle convergente ? - Si oui, quelle est sa limite ?
En cas de convergence de la suite ![]() vers un nombre complexe
vers un nombre complexe ![]() cette limite est notée :
cette limite est notée :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sigma=\sum_{k=0}^{\infty}u_{k}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7f1a4fcee3446207b24922777ae10787_l3.png)
Bien entendu, l’indexation ne démarre pas obligatoirement à 0 : on peut s’intéresser à la série ![]() et noter
et noter 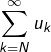 sa somme (en cas de convergence).
sa somme (en cas de convergence).
Dans de nombreux cas, il est possible de connaître la nature d’une série (c’est-à-dire : savoir si elle converge ou non). Il est, en revanche, assez exceptionnel que l’on puisse calculer explicitement la somme d’une série convergente, même si l’expression de ![]() est assez simple.
est assez simple.
Par exemple, la somme de la série convergente 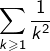 a été obtenue par Euler, près d’un siècle après que la question se soit posée (c’est le célèbre problème de Bâle). Après avoir développé une méthode d’accélération de la convergence (la célèbre formule d’Euler-MacLaurin), Euler observa que les développements décimaux illimités de cette somme de série et de
a été obtenue par Euler, près d’un siècle après que la question se soit posée (c’est le célèbre problème de Bâle). Après avoir développé une méthode d’accélération de la convergence (la célèbre formule d’Euler-MacLaurin), Euler observa que les développements décimaux illimités de cette somme de série et de ![]() semblaient coïncider, tout au moins sur une vingtaine de décimales. Il démontra en 1735 l’égalité :
semblaient coïncider, tout au moins sur une vingtaine de décimales. Il démontra en 1735 l’égalité :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=1}^{\infty}\frac{1}{k^{2}}=\frac{\pi^{2}}{6}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ccdad4ced3413ceb71ac496b1036e474_l3.png)
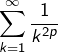 pour tout
pour tout En revanche, aucune formule explicite n’est connue à ce jour pour le nombre 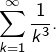
Quant à la série 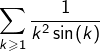 , on se sait même pas si elle est convergente ou divergente !
, on se sait même pas si elle est convergente ou divergente !
Terminons cette introduction en définissant le reste de rang ![]() d’une série convergente. Il s’agit de
d’une série convergente. Il s’agit de ![]() , c’est-à-dire :
, c’est-à-dire :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{R_n=\sum_{k=n+1}^\infty u_k}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d81a927976d25bb45a896ecc7149e8a2_l3.png)
2 – Séries géométriques
Etant donné un nombre complexe ![]() , il est connu que pour tout
, il est connu que pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n}q^{k}=\frac{1-q^{n+1}}{1-q}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-12ecc8b9e4183677da432f486e2c0331_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\sum_{k=0}^{n}q^{k}=\frac{1}{1-q}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f85602489c6f97d58d2454166e7de7c1_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=0}^{\infty}q^{k}=\frac{1}{1-q}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3775e20685623299d1a8676e56292863_l3.png)
Illustration dynamique
L’illustration dynamique ci-dessous fournit une interprétation visuelle des premières sommes partielles d’une somme géométrique. La raison ![]() varie dans
varie dans ![]() . Par conséquent, la somme
. Par conséquent, la somme ![]() varie entre
varie entre ![]() et
et ![]() ; elle est représenté par le rectangle bleu-ciel. Les termes successifs qui composent la somme partielle
; elle est représenté par le rectangle bleu-ciel. Les termes successifs qui composent la somme partielle
![Rendered by QuickLaTeX.com \[S_n=\sum_{k=0}^nq^k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0f33dc28a20a0437d4ced9e5b9d55434_l3.png)
3 – Développement décimal d’un réel
A la manière de Mr Jourdain, qui faisait de la prose sans le savoir, nous manipulons des séries convergentes depuis le collège !
En effet, lorsqu’on écrit le développement décimal illimité d’un nombre réel, par exemple :
![]()
![Rendered by QuickLaTeX.com \[\frac{1}{7}=\sum_{k=1}^{\infty}c_{k}10^{-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7fec92886e4a90277127f089d0d4eddd_l3.png)
![Rendered by QuickLaTeX.com \[c_{k}=\left\{ \begin{array}{ccc}1 & \text{si} & k\equiv1\pmod{6}\\4 & \text{si} & k\equiv2\pmod{6}\\2 & \text{si} & k\equiv3\pmod{6}\\8 & \text{si} & k\equiv4\pmod{6}\\5 & \text{si} & k\equiv5\pmod{6}\\7 & \text{si} & k\equiv0\pmod{6}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-102c2d787ded94db664258a09714fd74_l3.png)

4 – Télescopie
Dans certains cas, relativement exceptionnels, on est capable de calculer explicitement les sommes partielles de la série étudiée, ce qui ramène l’étude de celle-ci à un simple calcul de limite.
Un scénario typique est celui où les sommes partielles peuvent se mettre sous forme télescopique. Si vous n’êtes pas à l’aise avec cette notion, vous pouvez aller jeter un coup d’œil ici.
Voyons quelques exemples.
Exemple 1
On demande le calcul de :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{\infty}\frac{1}{k\left(k+1\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d330e3a80e4444047a83901224e78bf6_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\frac{1}{k\left(k+1\right)}=1-\frac{1}{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f9a599b4f8b057511ccf5e78591dfbb0_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=1}^{\infty}\frac{1}{k\left(k+1\right)}=1}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-608cf83eb5dee033ac0ea5b568d02f19_l3.png)
Exemple 2

Dans ce qui suit, on note ![]() la fonction arctangente.
la fonction arctangente.
On demande le calcul de :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{\infty}A\left(\frac{1}{\left(1+\sqrt{k\left(k+1\right)}\right)\left(\sqrt{k+1}+\sqrt{k}\right)}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42e26614d62238ed2fd70ed650f3fcda_l3.png)
Si l’on note, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[x_{k}=\frac{1}{\left(\sqrt{k\left(k+1\right)}+1\right)\left(\sqrt{k+1}+\sqrt{k}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b2409b8d62c846fc3a0401e75d99cc6c_l3.png)
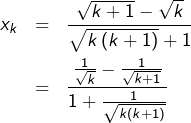
![]()
On obtient ainsi :
![]()
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}A\left(x_{k}\right)=A\left(1\right)-A\left(\frac{1}{\sqrt{n+1}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3672a61e1626c690670f310bfd6fa71e_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=1}^{\infty}A\left(\frac{1}{\left(1+\sqrt{k\left(k+1\right)}\right)\left(\sqrt{k+1}+\sqrt{k}\right)}\right)=\frac{\pi}{4}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a981ba5ff32b05f928b3487b20f7a3a8_l3.png)
Exemple 3
On demande le calcul, pour tout entier ![]() de :
de :
![Rendered by QuickLaTeX.com \[\sigma_{p}=\sum_{k=1}^{\infty}\frac{1}{k\left(k+1\right)\cdots\left(k+p\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dae5944fc51e8a47d2e15444be7a804e_l3.png)
Pour le cas général, on commence par expliquer que la série proposée converge, car la suite de ses sommes partielles est croissante (évident) et majorée par ![]()
On observe ensuite que, pour tous ![]() et
et ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[S_{n,p}=\sum_{k=1}^{n}\frac{1}{k\left(k+1\right)\cdots\left(k+p\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2caee0743696d4f3586fecca9f71c3f_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\sigma_{p}=\frac{1}{p\:p!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e2f5905652bec1195947dcdafd53c7f_l3.png)
Remarque
Dans ce calcul, on aurait pu s’attendre à une formule de récurrence, donnant ![]() en fonction de
en fonction de ![]() . Il est intéressant d’observer qu’on a directement obtenu une formule explicite pour
. Il est intéressant d’observer qu’on a directement obtenu une formule explicite pour ![]() : les
: les ![]() ont disparu lors du passage à la limite !
ont disparu lors du passage à la limite !
5 – Condition nécessaire de convergence
On pourrait penser que l’étude d’une série passe obligatoirement par le calcul explicite des sommes partielles, suivi d’un calcul de limite (si limite il y a …).
Il n’en est rien ! Et la raison principale est justement l’impossibilité, en général, d’obtenir une telle fomule explicite. A ce titre, l’exemple des séries géométriques présenté à la section 2 est exceptionnel.
On cherche plutôt à déterminer la nature d’une série en examinant seulement son terme général (et notamment le comportement asymptotique de celui-ci). Ceci est rendu possible par un cortège de règles de convergence qui seront, pour un petit nombre d’entre-elles, présentées dans cet article.
Voici la plus simple de toutes ces règles :
Condition Nécessaire de Convergence
Si une série ![]() converge, alors
converge, alors ![]()
La preuve est immédiate. Il suffit de voir que, pour tout ![]() :
:
![]()
Lorsque le terme général ne converge pas vers 0, la série est dite grossièrement divergente.
C’est par exemple le cas d’une série géométrique ![]() lorsque
lorsque ![]()
Mais attention ! La nature d’une série dont le terme général tend vers 0 n’est pas claire : une telle série peut converger ou diverger, selon les cas. Voici deux exemples de séries qui divergent, mais non grossièrement :
Exemple 1
La série 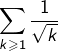 est divergente, bien que
est divergente, bien que ![]()
En effet, la somme partielle de rang ![]() comporte
comporte ![]() termes et le plus petit d’entre eux est
termes et le plus petit d’entre eux est ![]()
Il en résulte que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace\sum_{k=1}^{n}\frac{1}{\sqrt{k}}\geqslant n\times\frac{1}{\sqrt{n}}=\sqrt{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc243b37da6c96192cd842fd1508ef14_l3.png)
Exemple 2
La série harmonique ![]() est divergente, bien que
est divergente, bien que ![]()
Cet exemple et le précédent constituent des cas particuliers d’une situation générale (les séries de Riemann), étudiée à la section suivante.
Cela dit, pour la série harmonique, une minoration analogue à celle utilisée à l’exemple 1 ne donne rien. Voici ce qu’on peut néanmoins faire …
Posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e9e62ff52597157f7ef82d4b070212a_l3.png)
![Rendered by QuickLaTeX.com \[H_{2n}-H_{n}=\sum_{k=n+1}^{2n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-435cf17541d3018088c023746d4d83f1_l3.png)
![]()
6 – Les séries de Riemann (dans le champ réel)
Par définition, une série de Riemann est de la forme :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant1}\frac{1}{k^{s}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-446ef57932ed7bcf97a4b68112246b90_l3.png)
Il s’agit là d’une définition restreinte. Pour en savoir un peu plus, voir ici.
Nous allons montrer qu’elle converge si, et seulement si, ![]()
Il est déjà évident que la condition ![]() est nécessaire à la convergence puisque, dans le cas contraire, le terme général ne tend pas vers 0 (cf. section précédente).
est nécessaire à la convergence puisque, dans le cas contraire, le terme général ne tend pas vers 0 (cf. section précédente).
Proposition (nature des séries de Riemann)
Soit ![]() On note, pour tout
On note, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}\frac{1}{k^{s}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ae59696c5605f72cf987a02e44a7dfd_l3.png)
➣ Si ![]() alors :
alors :
![]()
➣ Si ![]() alors :
alors :
![]()
Il en résulte que la série 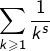 :
:
- converge si
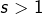
- diverge si
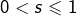
La clef de la démonstration réside dans une comparaison série / intégrale. L’application
![]()
![]()
Après sommation, il vient :
![]()
Quelle que soit la valeur du réel ![]() la suite
la suite ![]() est (strictement) croissante puisque :
est (strictement) croissante puisque :
![]()
- Si
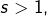 alors :
alors :
ce qui montre que la suite![Rendered by QuickLaTeX.com \[S_{n}\leqslant1+\frac{1}{s-1}\left(1-\frac{1}{n^{s-1}}\right)\leqslant\frac{s}{s-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5297819369863c6b99ab1a5c05068609_l3.png)
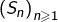 est majorée, donc convergente d’après le théorème de la limite monotone.
est majorée, donc convergente d’après le théorème de la limite monotone. - Si
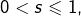 alors les minorations :
alors les minorations :
et![Rendered by QuickLaTeX.com \[S_{n}\geqslant\frac{1}{1-s}\left(\left(n+1\right)^{1-s}-1\right)\qquad\text{(pour }s<1)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-121112177b8cc1083a985f6a05ff642d_l3.png)
montre la divergence vers![Rendered by QuickLaTeX.com \[S_{n}\geqslant\ln\left(n+1\right)\qquad\text{(pour }s=1)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-882a7a2099c90ed6e217a415edd13c9d_l3.png)
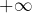 de la suite
de la suite 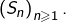
Maintenant que l’on dispose de séries « de référence », à savoir les séries géométriques et les séries de Riemann, on va mettre en place un outil de comparaison entre séries à termes positifs.
7 – Principe de comparaison
Proposition
Considérons deux suites ![]() et
et ![]() telles que :
telles que :
(![]() )
) ![]()
Dans ces conditions, la série ![]() est aussi convergente.
est aussi convergente.
Ce résultat, appelé Principe de Comparaison (PC en abrégé) pour les séries à termes positifs, joue un rôle central dans l’élaboration des règles usuelles de convergence. Voyons comment il se démontre.
Preuve (cliquer pour déplier / replier)
Considérons, pour tout ![]() les sommes partielles :
les sommes partielles :
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=0}^{n}a_{k}\qquad\text{et}\qquad B_{n}=\sum_{k=0}^{n}b_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5aa27e7d428c0539307e22c569125e9_l3.png)
![]()
![]()
Concernant le principe de comparaison, quelques remarques s’imposent :
- On peut l’énoncer sous forme contraposée : avec les mêmes hypothèses, la divergence de la série
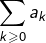 entraîne celle de la série
entraîne celle de la série 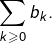
- Si les inégalités
 sont vraies APCR seulement, la conclusion est inchangée.
sont vraies APCR seulement, la conclusion est inchangée. - Si, sous les mêmes hypothèses, la série
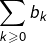 est divergente, on ne peut rien dire quant à la nature de la série
est divergente, on ne peut rien dire quant à la nature de la série 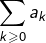 . Peut-être converge-t-elle et qu’on a majoré trop fort ? Ou alors elle diverge … et dans ce cas, il faudrait plutôt chercher à minorer
. Peut-être converge-t-elle et qu’on a majoré trop fort ? Ou alors elle diverge … et dans ce cas, il faudrait plutôt chercher à minorer 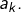
Voici trois exemples d’utilisation :
Exemple 1
On demande la nature de la série :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant1}\frac{\left|\cos\left(k\right)\right|}{k^{2}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7b90e6b167c46c4971bdbf73ab80840b_l3.png)
![]()
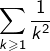 converge, alors la série proposée aussi, d’après le principe de comparaison.
converge, alors la série proposée aussi, d’après le principe de comparaison.
Exemple 2
On demande la nature de la série :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant1}\left(1-e^{-1/k}\right)}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-741f9a5751d9b0ec2d41e68c8fe3f045_l3.png)
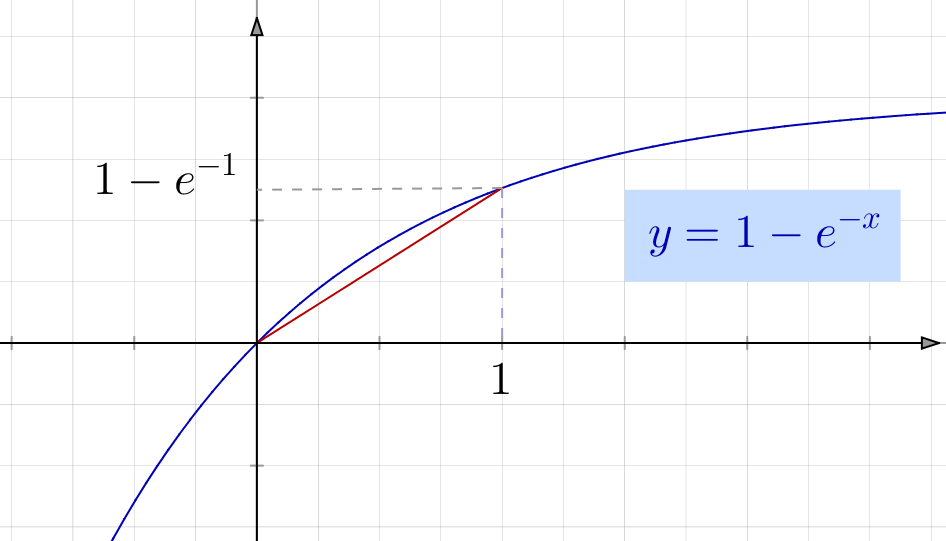
Il en résulte qu’en posant ![]() :
:
![]()
![]()
Remarque
Il est nettement plus simple d’aborder cet exemple en utilisant la règle des équivalents (voir plus bas), puisque :
![]()
Exemple 3
On demande la nature de la série :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant2}\frac{\ln\left(k\right)}{k^{2}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2e4193c011a71866305fe29eca035cf2_l3.png)
![]()
Nous allons « consommer » un peu de l’exposant 2 et faire apparaître le produit d’un facteur borné par le terme général d’une série de Riemann convergente :
![]()
![]()
![]()
8 – Premier corollaire du principe de comparaison
Règle de d’Alembert
Etant donnée une suite ![]() à termes strictement positifs, on suppose qu’il existe un réel
à termes strictement positifs, on suppose qu’il existe un réel ![]() tel que :
tel que :
![]()
- si
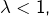 la série
la série 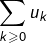 converge,
converge, - si
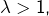 la série
la série 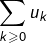 diverge grossièrement.
diverge grossièrement.
Dans le cas où ![]() la nature de la série
la nature de la série ![]() reste indéterminée (on parle du cas douteux de la règle de d’Alembert).
reste indéterminée (on parle du cas douteux de la règle de d’Alembert).
En anglais, cette règle est connue sous le nom de ratio’s test.
On peut établir ce résultat en comparant ![]() au terme général d’une suite géométrique.
au terme général d’une suite géométrique.
Preuve (cliquer pour déplier / replier)
➣ Traitons d’abord le cas où ![]() et choisissons un réel
et choisissons un réel ![]()
Vu que la suite ![]() converge vers
converge vers ![]() il existe un entier
il existe un entier ![]() tel que :
tel que :
![]()
![Rendered by QuickLaTeX.com \[\prod_{k=N}^{n-1}\frac{u_{k+1}}{u_{k}}\leqslant\mu^{n-N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b72a492fda332c2d3d3d8024d5d92a4e_l3.png)
![]()
![]()
➣ Passons au cas ![]() Le raisonnement est analogue, quoique plus simple.
Le raisonnement est analogue, quoique plus simple.
Il existe un entier ![]() tel que :
tel que :
![]()
➣ Enfin, il est impossible de conclure (sans plus d’information) lorsque ![]() Il suffit, pour s’en convaincre, d’exhiber deux séries à termes strictement positifs pour lesquelles
Il suffit, pour s’en convaincre, d’exhiber deux séries à termes strictement positifs pour lesquelles ![]() l’une étant convergente et l’autre étant divergente. C’est par exemple le cas des séries de Riemann (voir section 6) :
l’une étant convergente et l’autre étant divergente. C’est par exemple le cas des séries de Riemann (voir section 6) :
![Rendered by QuickLaTeX.com \[\sum_{k\geqslant1}\frac{1}{k^{2}}\qquad\text{et}\qquad\sum_{k\geqslant1}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aeb1aff3beeee734410d6f8987394f4c_l3.png)
Voici trois exemples d’utilisation de la règle de d’Alembert.
Exemple 1
Etant donnés ![]() on demande la nature de la série :
on demande la nature de la série :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant1}\frac{a^{k}}{k^{b}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c81c4598934810fc478d296275e070a2_l3.png)
![]()
Pour ![]() on reconnaît une série de Riemann, qui converge si et seulement si
on reconnaît une série de Riemann, qui converge si et seulement si ![]()
Exemple 2
Etant donné ![]() on demande la nature de la série :
on demande la nature de la série :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant0}\frac{x^{k}}{k!}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-55bad88beff661e16687c7e0c416d371_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=0}^{\infty}\frac{x^{k}}{k!}=e^{x}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fefa42d6a054ec64639c3a4f466c3d20_l3.png)
Exemple 3
On demande la nature de la série de terme général :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{u_{k}=\frac{k!}{k^{k}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01e35721105d3358dc8839c808aa96a4_l3.png)
![Rendered by QuickLaTeX.com \[\frac{u_{k+1}}{u_{k}}=\frac{\left(k+1\right)!}{\left(k+1\right)^{k+1}}\:\frac{k^{k}}{k!}=\left(\frac{k}{k+1}\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-178008698f1d3ae272fe3a9a7c7b0146_l3.png)
![]()
![]()
Notons qu’on pouvait se contenter du principe de comparaison, puisque pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[0<u_{k}=\prod_{j=1}^{k}\frac{j}{k}=\frac{2}{k^{2}}\prod_{j=3}^{k}\frac{j}{k}\leqslant\frac{2}{k^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3d706c076f5b98717e25cdc39df19ef6_l3.png)
Un sérieuse mise en garde :

Si ![]() pour tout
pour tout ![]() et si la série
et si la série ![]() converge, il n’est pas du tout certain que la suite
converge, il n’est pas du tout certain que la suite ![]() converge vers une limite
converge vers une limite ![]() . Tout au plus peut-on dire que SI elle converge, alors sa limite appartient à ce segment.
. Tout au plus peut-on dire que SI elle converge, alors sa limite appartient à ce segment.
Sauriez-vous trouver un exemple de série convergente, à termes strictement positifs et telle que la suite ![]() soit divergente ? Solution en annexe.
soit divergente ? Solution en annexe.
9 – Second corollaire du principe de comparaison
Dans ce qui suit, nous aurons besoin de la notion de suites réelles équivalentes.
Rappelons ce dont il s’agit :
Définition
Deux suites réelles ![]() et
et ![]() dont les termes sont tous non nuls (au moins APCR) sont dites équivalentes lorsque :
dont les termes sont tous non nuls (au moins APCR) sont dites équivalentes lorsque :
![]()
![]()
On peut maintenant énoncer :
Règle des équivalents
Soient ![]() et
et ![]() deux séries à termes strictement positifs.
deux séries à termes strictement positifs.
Si de plus ![]() alors les deux séries sont de même nature.
alors les deux séries sont de même nature.
Preuve (cliquer pour déplier / replier)
L’hypothèse ![]() entraîne l’existence d’un entier
entraîne l’existence d’un entier ![]() tel que :
tel que :
![]()
![]()
Exemple 1
On demande la nature de la série de terme général :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{u_{n}=\frac{e^{1/n}}{n}\sin^{2}\left(\frac{1}{\sqrt{n}}\right)}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2bb1d97ceb2eac5cbfd6d5e55f7a67b2_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{u_{n}\sim\frac{1}{n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8ecf091ea80129974a6e267b190fccd_l3.png)
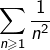 converge, on conclut avec la règle des équivalents que la série proposée converge aussi.
converge, on conclut avec la règle des équivalents que la série proposée converge aussi.
Exemple 2
On demande la nature de la série de terme général :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{u_{n}=e-\left(1+\frac{1}{n}\right)^{n}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a3af59e828517cee914ce6d8fff47c5_l3.png)
![]()
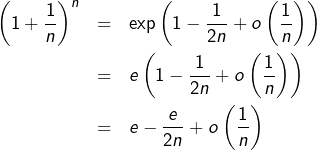
![]()
Exemple 3
On demande la nature de la série de terme général :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{u_{n}=\left(\sum_{k=n}^{\infty}\frac{1}{k^{\alpha}}\right)^{\beta}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbc16ca1ca05f1dcf6f3aec05e8254d7_l3.png)
On va, là encore, obtenir un équivalent de ![]() ce qui permettra de conclure. Pour cela, on commence par trouver un équivalent du reste :
ce qui permettra de conclure. Pour cela, on commence par trouver un équivalent du reste :
![Rendered by QuickLaTeX.com \[R_{n}=\sum_{k=n}^{\infty}\frac{1}{k^{\alpha}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b1b05f1f5891b51a5ac853ca9533fac0_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\int_{n}^{p+1}\frac{dx}{x^{\alpha}}\leqslant\sum_{k=n}^{p}\frac{1}{k^{\alpha}}\leqslant\int_{n-1}^{p}\frac{dx}{x^{\alpha}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-30615bc61c4305971ef35c2043805cff_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\frac{1}{\left(\alpha-1\right)n^{\alpha-1}}\leqslant R_{n}\leqslant\frac{1}{\left(\alpha-1\right)\left(n-1\right)^{\alpha-1}}=\frac{1}{\left(\alpha-1\right)n^{\alpha-1}\left(1-\frac{1}{n}\right)^{\alpha-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9b53096dcb8cab14dd057e87710ad526_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{R_{n}\sim\frac{1}{\left(\alpha-1\right)n^{\alpha-1}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-12f696050703aa7442b053fe2655cdb3_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{u_{n}\sim\frac{1}{\left(\alpha-1\right)^{\beta}}\thinspace\frac{1}{n^{\left(\alpha-1\right)\beta}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ee6b0ba5edbb8bd7c60c7524e9f561c8_l3.png)
Exemple 4
On demande la nature de la série :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k\geqslant1}\frac{\left(2k\right)!}{4^{k}\left(k!\right)^{2}}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2a517c864af78345b5212317eae2d215_l3.png)
![Rendered by QuickLaTeX.com \[\frac{u_{k+1}}{u_{k}}=\frac{\left(2k+2\right)!}{4^{k+1}\left(\left(k+1\right)!\right)^{2}}\thinspace\frac{4^{k}\left(k!\right)^{2}}{\left(2k\right)!}=\frac{\left(2k+2\right)\left(2k+1\right)}{4\left(k+1\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-116eede655d36cf47d8c735a914131be_l3.png)
![]()
Mais on s’en sort en reconnaissant une intégrale de Wallis. Il est en effet classique qu’en posant, pour tout ![]() :
:
![]()
![]()
![]()
![]()
Remarque
On pourrait aussi conclure en appliquant la règle de Raabe-Duhamel, qui sera présenté dans un prochain article.
Dans cette première partie, on a présenté quelques généralités sur les séries et l’essentiel de ce qu’il faut savoir concernant les séries à termes réels positifs. Dans la seconde partie, on examine les séries à termes réels de signe quelconque et, plus généralement, à termes complexes.
Annexe
A la fin de la section 8, on a demandé un exemple de série convergente, à termes strictement positifs, pour laquelle la suite ![]() diverge. Voici un tel exemple :
diverge. Voici un tel exemple :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{u_k=\left\{\begin{matrix}2^{-k} & \text{si }k\text{ est pair}\\3^{-k} & \text{sinon}\end{matrix}\right.}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-073fd179c5970ffe9b06331375dac9c6_l3.png)
![]()
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonjour Monsieur,
Merci pour cet article qui remet plusieurs idées en place !
(tout à la fin de la partie 1, un « semblait » s’est glissé à la place de « semblaient », et je crois qu’il s’agit de k supérieur ou égal à 1 pour la série dont on ne sait pas si elle diverge).
Bien à vous,
Fabrice
Évidemment ! Merci de m’avoir signalé ces coquilles, qui sont à présent corrigées.