
Cet article est une introduction à l’étude des intégrales impropres.
Le contexte a été restreint aux applications continues sur un intervalle, à valeurs réelles. Cette limitation n’empêchera pas de mettre en évidence les principaux aspects du sujet.
On suppose connues les propriétés de base de l’intégrale d’une application continue, définie sur un segment (intervalle fermé borné) et à valeurs réelles : linéarité, positivité, inégalité du module, relations de Chasles, … On pourra se reporter à cet article pour consulter les énoncés détaillés de chacune de ces propriétés.
Dans un premier temps (sections 1 à 6), on se limite à des intégrales de la forme ![]() Cette restriction temporaire permet à celles et ceux qui ne sont pas déjà familiarisés avec le sujet, d’y pénétrer plus facilement. Le cadre est ensuite élargi, autorisant un intervalle d’intégration quelconque et des intégrales multiplement impropres.
Cette restriction temporaire permet à celles et ceux qui ne sont pas déjà familiarisés avec le sujet, d’y pénétrer plus facilement. Le cadre est ensuite élargi, autorisant un intervalle d’intégration quelconque et des intégrales multiplement impropres.
1 – Notion d’intégrale impropre
Considérons une application continue ![]() le réel
le réel ![]() étant fixé.
étant fixé.
Pour tout ![]() on définit l’intégrale partielle de
on définit l’intégrale partielle de ![]() sur
sur ![]() :
:
![]()
![]()
Le symbole ![]() désigne donc deux choses à la fois :
désigne donc deux choses à la fois :
- d’une part, l’intégrale impropre en tant qu’objet algébrique, qu’elle soit convergente ou divergente,
- d’autre part, la fameuse limite
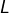 (en cas de convergence), qui est un nombre réel.
(en cas de convergence), qui est un nombre réel.
Cette ambiguïté n’est pas gênante, car le contexte permet toujours de s’y retrouver.
Procédure de base :
Pour déterminer si une intégrale impropre donnée est convergente ou non, la procédure la plus simple consiste, lorsque c’est possible, à :
- calculer d’abord l’intégrale partielle de façon explicite,
- examiner ensuite si celle-ci admet (ou non) une limite finie en
Toutefois, le calcul explicite de l’intégrale partielle est généralement hors de portée, ce qui limite cette procédure aux cas les plus simples.
Malgré cela, il reste souvent possible de préciser la nature d’une intégrale impropre et même (quoique beaucoup plus rarement) d’en calculer explicitement la valeur en cas de convergence, même si l’on ne sait pas expliciter l’intégrale partielle (voir l’exemple 4 ci-dessous) !
Exemple 1
Considérons :
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{+\infty}t\thinspace e^{-t}\thinspace dt=1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-32df58dc2b4a8e693d524f8e78428a8f_l3.png)
Exemple 2
Considérons maintenant :
![]()
![]()
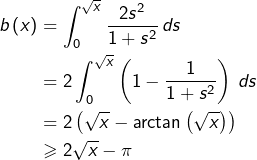
Ainsi, ![]() et l’intégrale impropre
et l’intégrale impropre ![]() est donc divergente.
est donc divergente.
Exemple 3
Considérons encore :
![]()
![]()
Il s’agit donc d’une intégrale divergente, quoique d’un style différent du précédent.
Exemple 4
Pour chacun des exemples 1 à 3, il était facile de calculer explicitement l’intégrale partielle. A présent, intéressons-nous à :
![]()
Pour autant, la question de savoir si ![]() admet en
admet en ![]() une limite finie (ou non) reste posée. Et la réponse est intéressante, à plus d’un titre !
une limite finie (ou non) reste posée. Et la réponse est intéressante, à plus d’un titre !
On peut en effet montrer que l’intégrale impropre ![]() (appelée intégrale de Gauss, encore que cette dénomination soit discutable …) est convergente et, plus précisément, que :
(appelée intégrale de Gauss, encore que cette dénomination soit discutable …) est convergente et, plus précisément, que :
![]()
Si l’étude de cette intégrale vous intéresse, je vous invite à jeter un œil à l’exercice n° 6 de cette fiche.
2 – Comparaison de fonctions positives
Principe de comparaison
Soient ![]() deux applications continues telles que :
deux applications continues telles que :
![]()
Si l’intégrale impropre ![]() converge, alors il en va de même pour
converge, alors il en va de même pour ![]() .
.
Une simple inégalité peut donc suffire pour établir la convergence d’une intégrale impropre, sans avoir à calculer l’intégrale partielle associée (ce qui, comme on l’a dit, n’est pas faisable en général) et encore moins la limite éventuelle de celle-ci.
Si vous connaissez déjà le principe de comparaison pour les séries numériques à termes positifs, vous constaterez la profonde analogie entre les deux énoncés.
Le principe de comparaison repose pour l’essentiel sur le théorème de la limite monotone, qui est l’analogue, pour les fonctions, du célèbre « toute suite réelle, croissante et majorée, est convergente« .
En voici une preuve détaillée :
Preuve (cliquer pour déplier / replier)
Posons, pour tout ![]() :
:
![]()
![]()
Comme ![]() est croissante (en raison de la positivité de
est croissante (en raison de la positivité de ![]() on voit que
on voit que ![]() (il suffit de choisir
(il suffit de choisir ![]() et d’effectuer un passage à la limite dans l’inégalité
et d’effectuer un passage à la limite dans l’inégalité ![]() lorsque
lorsque ![]() Ainsi, pour tout
Ainsi, pour tout ![]() :
:
![]()
La convergence de l’intégrale impropre ![]() est établie.
est établie.
En outre, en notant ![]() un simple passage à la limite dans l’inégalité
un simple passage à la limite dans l’inégalité ![]() montre que
montre que ![]()
Ajoutons quelques remarques, qui viennent nuancer cette proposition.
Remarque 1
La nature (convergence ou divergence) de l’intégrale impropre ![]() ne dépend que du comportement de
ne dépend que du comportement de ![]() au voisinage de
au voisinage de ![]()
En particulier, si la condition ![]() est remplacée par la condition plus faible :
est remplacée par la condition plus faible :
![]()
Remarque 2
Si ![]()
![]() et si
et si ![]() diverge, on ne peut rien dire de la nature de
diverge, on ne peut rien dire de la nature de ![]() Cette dernière intégrale peut, selon les cas, converger ou diverger.
Cette dernière intégrale peut, selon les cas, converger ou diverger.
Remarque 3
Si ![]() et si
et si ![]() diverge, alors
diverge, alors ![]() diverge aussi. C’est la forme contraposée du principe de comparaison.
diverge aussi. C’est la forme contraposée du principe de comparaison.
3 – Intégrales de référence
Disposer d’un principe de comparaison n’a d’intérêt que si l’on dispose aussi de fonctions positives (et continues sur ![]() ) pour lesquelles la nature de l’intégrale impropre est connue.
) pour lesquelles la nature de l’intégrale impropre est connue.
On parle alors d’intégrales de référence … ce qui, au fond, ne veut rien dire car l’étendue de cette classe peut varier d’un cours à l’autre ! Néanmoins, tout le monde s’accorde pour y inclure, au minimum, les intégrales de la forme :
![]()
Certains les appellent à tort « intégrales de Riemann », sans doute par glissement sémantique, vu que les séries 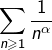 sont officiellement dénommées « séries de Riemann ». En outre, l’expression « intégrale de Riemann » désigne tout à fait autre chose …
sont officiellement dénommées « séries de Riemann ». En outre, l’expression « intégrale de Riemann » désigne tout à fait autre chose …
Proposition
Etant donné ![]() l’intégrale
l’intégrale ![]() converge si, et seulement si
converge si, et seulement si ![]()
Preuve (cliquer pour déplier / replier)
Supposons d’abord ![]() Pour tout
Pour tout ![]() :
:
![]()
- Si
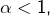 alors
alors 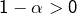 donc
donc 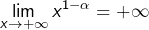 et donc
et donc ![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow+\infty}\int_{a}^{x}\frac{1}{t^{\alpha}}\thinspace dt=+\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-937ba7386d9d2cb48c653847c7be192c_l3.png)
- Si
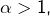 alors
alors 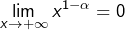 et donc
et donc ![Rendered by QuickLaTeX.com \[ \lim_{x\rightarrow+\infty}\int_{a}^{x}\frac{1}{t^{\alpha}}\thinspace dt=\frac{1}{\left(\alpha-1\right)a^{\alpha-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f4278c6f4d733bcc11cb9658136c9d1c_l3.png)
Enfin, si ![]() l’intégrale partielle prend la forme
l’intégrale partielle prend la forme ![]() et donc
et donc
![]()
Il est courant d’inclure aussi les intégrales de la forme ![]() (avec
(avec ![]() et
et ![]() a priori quelconque). Afin d’alléger la présentation, on se contentera ici d’un énoncé (pour les détails, voir l’exercice n° 4 de cette fiche).
a priori quelconque). Afin d’alléger la présentation, on se contentera ici d’un énoncé (pour les détails, voir l’exercice n° 4 de cette fiche).
Proposition (intégrales de Bertrand)
Etant donné ![]() l’intégrale impropre
l’intégrale impropre
![Rendered by QuickLaTeX.com \[\int_{a}^{+\infty}\frac{1}{t^{\alpha}\ln^{\beta}\left(t\right)}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-75be39d957aabfbe21051cc5fe35c553_l3.png)
![]()
4 – Règle des équivalents
Proposition
Soient ![]() continues.
continues.
On suppose que :
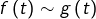 lorsque
lorsque 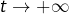
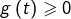 pour
pour 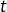 assez grand.
assez grand.
Alors les intégrales ![]() et
et ![]() sont de même nature (ce qui signifie qu’elles sont toutes les deux convergentes ou bien toutes les deux divergentes).
sont de même nature (ce qui signifie qu’elles sont toutes les deux convergentes ou bien toutes les deux divergentes).
Preuve (cliquer pour déplier / replier)
Comme ![]() lorsque
lorsque ![]() il existe
il existe ![]() tel que :
tel que :
![]()
En cas de divergence de ![]() on voit de même que
on voit de même que ![]() diverge (avec l’inégalité de gauche cette fois).
diverge (avec l’inégalité de gauche cette fois).
Exemple 1
Quelle est la nature de l’intégrale 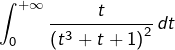 ?
?
Comme :
![]()
Exemple 2
Quelle est la nature de l’intégrale ![]() ?
?
Au voisinage de ![]() :
:
![]()
![]()
Exemple 3
Quelle est la nature de l’intégrale 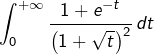 ?
?
Au voisinage de ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{1+e^{-t}}{\left(1+\sqrt{t}\right)^{2}}\sim\frac{1}{t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f9881fd5c6b8570830acf055684a74a4_l3.png)
Parmi les hypothèses de la règle des équivalents, figure la condition : ![]() pour
pour ![]() assez grand.
assez grand.
Cette condition peut évidemment être remplacée par : ![]() pour
pour ![]() assez grand. En clair, on demande à
assez grand. En clair, on demande à ![]() d’être de signe constant au voisinage de
d’être de signe constant au voisinage de ![]() (ce qui impose la même chose à
(ce qui impose la même chose à ![]() puisque l’équivalence préserve localement le signe).
puisque l’équivalence préserve localement le signe).

Mais attention, sans aucune condition de signe, notre brave règle des équivalents ne s’applique plus !
Voir la section 6 pour un contre-exemple.
5 – Convergence absolue
Considérons une application continue ![]()
Définition
L’intégrale impropre ![]() est dite absolument convergente lorsque l’intégrale
est dite absolument convergente lorsque l’intégrale ![]() est convergente.
est convergente.
Le résultat suivant est fondamental :
Théorème
Si l’intégrale ![]() est absolument convergente, alors elle est convergente.
est absolument convergente, alors elle est convergente.
Preuve (cliquer pour déplier / replier)
On constate que ![]() mais bien entendu, il n’est pas question d’appliquer le principe de comparaison de cette façon, puisqu’on n’a pas la positivité du membre de gauche !
mais bien entendu, il n’est pas question d’appliquer le principe de comparaison de cette façon, puisqu’on n’a pas la positivité du membre de gauche !
Toutefois, en y regardant de plus près, cette majoration peut aussi s’écrire :
![]()
On peut donc finalement appliquer le principe de comparaison : l’intégrale impropre ![]() étant convergente, il en va de même de
étant convergente, il en va de même de ![]() et donc, par différence, l’intégrale
et donc, par différence, l’intégrale ![]() est convergente. CQFD.
est convergente. CQFD.
Voyons un exemple d’utilisation.
Exemple
Quelle est la nature de l’intégrale ![]() ?
?
Il suffit d’observer que :
![]()
Facile, n’est-ce pas ? Mais attention, la réciproque de la proposition précédente est fausse : il existe des intégrales convergentes, mais non absolument convergentes. De telles intégrales sont dites semi-convergentes. La section 7 en donne un exemple détaillé.
6 – Deux intégrales de natures distinctes, malgré l’équivalence
Commençons par nous intéresser à l’intégrale impropre :
![]()
![]()
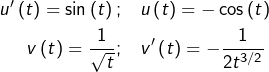
![]()
![]()
![]()
Comme ![]() on voit que l’intégrale
on voit que l’intégrale ![]() est absolument convergente, donc convergente (voir section précédente). De ce fait, on peut poser :
est absolument convergente, donc convergente (voir section précédente). De ce fait, on peut poser :
![]()
![]()
Nous avons établi que l’intégrale ![]() est convergente. Considérons maintenant l’intégrale impropre :
est convergente. Considérons maintenant l’intégrale impropre :
![]()
![Rendered by QuickLaTeX.com \[\frac{\sin\left(t\right)}{\sqrt{t}+\sin\left(t\right)}=\frac{\sin\left(t\right)}{\sqrt{t}}\:\frac{1}{1+\frac{\sin\left(t\right)}{\sqrt{t}}}\sim\frac{\sin\left(t\right)}{\sqrt{t}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5df35cc5e0fc7d23173fe61dd0c5d355_l3.png)

En appliquant la règle des équivalents à ce cas de figure, on conclurait que les intégrales ![]() et
et ![]() sont de même nature, autrement dit que
sont de même nature, autrement dit que ![]() est convergente.
est convergente.
Mais il n’en est rien !
En effet, lorsque ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\frac{\sin\left(t\right)}{\sqrt{t}+\sin\left(t\right)}=\boxed{\frac{\sin\left(t\right)}{\sqrt{t}}}_{\;\color{red}1}-\boxed{\frac{\sin^{2}\left(t\right)}{t}}_{\;\color{red}2}+\boxed{O\left(\frac{1}{t^{3/2}}\right)}_{\;\color{red}3}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-10a18cd0f8d281bc52f074181407fe77_l3.png)
La première, donne une intégrale convergente comme on l’a déjà expliqué (il s’agit de ![]() et la troisième donne une intégrale absolument convergente (si une fonction continue
et la troisième donne une intégrale absolument convergente (si une fonction continue ![]() vérifie
vérifie ![]() lorsque
lorsque ![]() alors il existe
alors il existe ![]() tel que
tel que
![]()
![]()
L’intégrale ![]() est donc bien divergente. Résumons :
est donc bien divergente. Résumons :
Si ![]() sont deux applications continues, alors les intégrales impropres
sont deux applications continues, alors les intégrales impropres ![]() et
et ![]() peuvent être de natures différentes, même si
peuvent être de natures différentes, même si ![]() au voisinage de
au voisinage de ![]()
Pour que la règle des équivalents (cf. section 4) soit applicable, il est indispensable que l’une des deux fonctions soit localement de signe constant (ce qui impose la même propriété pour l’autre).
Précisons que « localement » signifie ici : sur ![]() pour
pour ![]() assez grand.
assez grand.
7 – Intégrales semi-convergentes
On examine dans cette section un exemple détaillé d’intégrale semi-convergente, c’est-à-dire convergente mais non absolument convergente.
Reprenons l’intégrale ![]() introduite au début de la section 6. Nous avons établi sa convergence. Montrons maintenant que l’intégrale
introduite au début de la section 6. Nous avons établi sa convergence. Montrons maintenant que l’intégrale ![]() diverge. En posant, pour tout
diverge. En posant, pour tout ![]() :
:
![]()
![]()
On peut envisager deux méthodes …
– Méthode 1 –
On va montrer que ![]() ce qui permettra de conclure puisque
ce qui permettra de conclure puisque ![]() est croissante (intégrale partielle d’une fonction positive).
est croissante (intégrale partielle d’une fonction positive).
Pour tout entier ![]() la relation de Chasles donne :
la relation de Chasles donne :
![Rendered by QuickLaTeX.com \[g\left(n\pi\right)=\sum_{k=1}^{n-1}\int_{k\pi}^{\left(k+1\right)\pi}\frac{\left|\sin\left(t\right)\right|}{\sqrt{t}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-db2d8103806bd9d35b87346bd52d2368_l3.png)
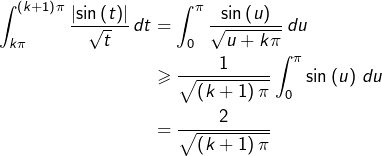
![Rendered by QuickLaTeX.com \[g\left(n\pi\right)\geqslant\frac{2}{\sqrt{\pi}}\sum_{k=2}^{n}\frac{1}{\sqrt{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5ff00cc3356a69be296a210d227d873_l3.png)
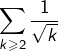 diverge.
diverge.
– Méthode 2 –
On exploite le fait que ![]()
Ainsi, pour tout ![]() et via une formule de linéarisation :
et via une formule de linéarisation :
![]()
![]()
![]()
On en déduit le résultat attendu : ![]()
8 – Cas d’un intervalle d’intégration semi-ouvert borné
On s’est restreint, depuis le début de cet article, à des intégrales de fonctions continues sur des intervalles de la forme ![]()
Autrement dit, les intégrales considérées étaient impropres pour la borne ![]() On change maintenant le fusil d’épaule …
On change maintenant le fusil d’épaule …
Etant donnés deux réels ![]() et
et ![]() continue, posons pour tout
continue, posons pour tout ![]() :
:
![]()
Si cette limite existe et est finie, l’intégrale ![]() (qui est impropre pour la borne
(qui est impropre pour la borne ![]() est dite convergente et ce symbole désigne aussi la limite en question.
est dite convergente et ce symbole désigne aussi la limite en question.
Signalons pour commencer que si ![]() possède en
possède en ![]() une limite finie
une limite finie ![]() , il suffit de prolonger
, il suffit de prolonger ![]() par continuité en
par continuité en ![]() , en posant
, en posant
![]()
Exemple
L’intégrale :
![]()
Les choses deviennent plus intéressantes lorsqu’un tel prolongement par continuité n’est pas possible. C’est typiquement le cas lorsque ![]() (mais il se peut aussi que
(mais il se peut aussi que ![]() n’admette tout simplement pas de limite en
n’admette tout simplement pas de limite en ![]() ).
).
Par exemple, l’intégrale ![]() (qui est impropre pour la borne 0) est convergente car :
(qui est impropre pour la borne 0) est convergente car :
![]()
On peut alors énoncer un principe de comparaison, très semblable à celui présenté à la section 2 :
Principe de comparaison (bis)
Soient ![]() deux applications continues telles que :
deux applications continues telles que :
![]()
Si l’intégrale impropre ![]() converge, alors il en va de même pour
converge, alors il en va de même pour ![]()
Comme expliqué à la section 3, il nous faut des intégrales « de référence » !
Voici le minimum syndical :
Proposition
L’intégrale impropre :
![]()
Par exemple, pour l’intégrale ![]() on peut voir que :
on peut voir que :
![]()
On dispose aussi d’une règle des équivalents (conséquence du principe de comparaison) :
Règle des équivalents (bis)
Soient ![]() continues. On suppose que
continues. On suppose que ![]() lorsque
lorsque ![]()
On suppose en outre que ![]() pour
pour ![]() assez proche de
assez proche de ![]() Alors les intégrales
Alors les intégrales ![]() et
et ![]() sont de même nature (ce qui signifie qu’elles sont toutes les deux convergentes ou bien toutes les deux divergentes).
sont de même nature (ce qui signifie qu’elles sont toutes les deux convergentes ou bien toutes les deux divergentes).
Par exemple, pour l’intégrale ![]() on observe que :
on observe que :
![]()
9 – Intégrales multiplement impropres
Evitons ici les généralités abstraites et contentons-nous d’exemples pour comprendre de quoi il retourne. L’intégrale
![]()
Pour traiter cette situation, on partage l’intervalle d’intégration. On considère les deux intégrales (simplement) impropres :
![]()
Il s’agit alors de déterminer la nature de ![]() et de
et de ![]()
➡ L’intégrale ![]() sera déclarée convergente à condition que
sera déclarée convergente à condition que ![]() et
et ![]() le soient.
le soient.
Il se trouve que c’est le cas. En effet, l’équivalent
![]()
![]()
Maintenant, généralisons et considérons pour tout réel ![]() l’intégrale :
l’intégrale :
![]()
L’intégrale ![]() précédente correspondait au cas particulier
précédente correspondait au cas particulier ![]()
Si ![]() cette intégrale est impropre pour la borne
cette intégrale est impropre pour la borne ![]() seulement. Pour établir sa convergence, on peut observer que
seulement. Pour établir sa convergence, on peut observer que ![]() (propriété bien connue de l’exponentielle qui « l’emporte », au voisinage de
(propriété bien connue de l’exponentielle qui « l’emporte », au voisinage de ![]() sur toute fonction puissance d’exposant fixe), ce qui entraîne l’existence d’un réel
sur toute fonction puissance d’exposant fixe), ce qui entraîne l’existence d’un réel ![]() tel que :
tel que :
![]()
![]()
Mais si ![]() cette intégrale est doublement impropre (un problème en 0 s’est ajouté à celui en
cette intégrale est doublement impropre (un problème en 0 s’est ajouté à celui en ![]() Là encore, on considère séparément les intégrales :
Là encore, on considère séparément les intégrales :
![]()
![]()
Et pour la seconde, la convergence a déjà été prouvée ci-dessus (cf. majoration ![]()
On peut donc conclure :
![]()
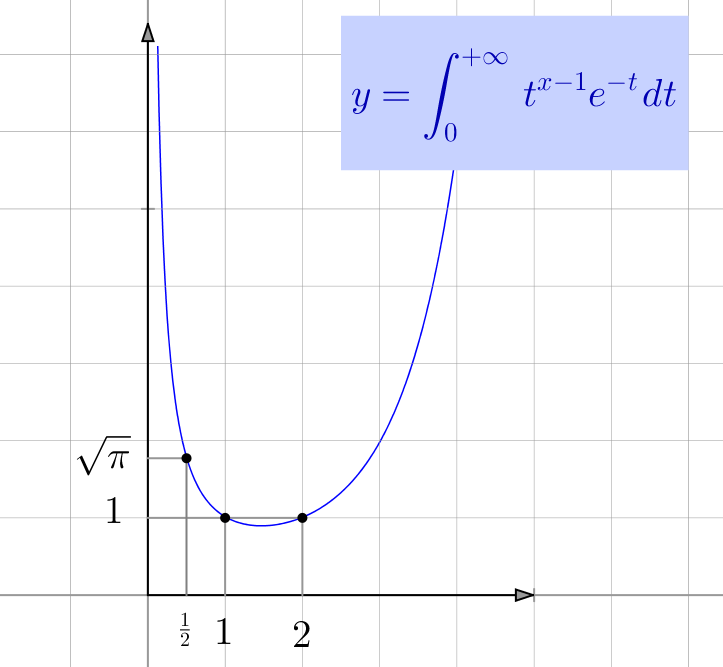
Précisons que cet exemple n’a rien d’anecdotique. Il s’agit de la célèbre fonction Gamma d’Euler :
![Rendered by QuickLaTeX.com \[\boxed{\forall x>0,\thinspace\Gamma\left(x\right)=\int_{0}^{+\infty}t^{x-1}e^{-t}\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d1d4819081d19f003239c69beb38b85_l3.png)
![]()
Quant à l’intégrale ![]() du début, elle est étroitement liée à l’intégrale de Gauss (cf. fin de la section 1), puisque le changement de variable
du début, elle est étroitement liée à l’intégrale de Gauss (cf. fin de la section 1), puisque le changement de variable ![]() donne :
donne :
![]()
Voici, à titre indicatif, l’allure du graphe de la fonction ![]() :
:
10 – Une condition ni nécessaire ni suffisante
Les intégrales impropres et les séries numériques se ressemblent beaucoup, au moins par certains aspects :
- définition par l’existence d’une limite finie pour l’intégrale ou la somme partielle,
- principe de comparaison et règle des équivalents,
- convergence absolue …
Mais il existe aussi des différences notables. On connaît par exemple la :
Condition nécessaire de convergence (pour les séries numériques)
Soit ![]() une suite réelle.
une suite réelle.
Si la série ![]() converge, alors
converge, alors ![]()
La preuve de cette proposition est simple. Si l’on note ![]() la
la ![]() -ème somme partielle, définie par :
-ème somme partielle, définie par :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^{\star},\thinspace S_{n}=\sum_{k=1}^{n}a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c21142b2028b6e17ff7a9ce220979ca_l3.png)
![]()
Mais pour les intégrales impropres, rien de tel !
Proposition
Etant donnée ![]() continue, il n’existe AUCUN LIEN entre :
continue, il n’existe AUCUN LIEN entre :
- la convergence de l’intégrale impropre
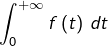
- le fait que
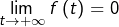
Pour justifier cette affirmation, nous allons devoir exhiber :
- un premier exemple où l’intégrale diverge, bien que
 tende vers 0 en
tende vers 0 en 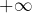
- un second exemple ou l’intégrale converge, bien que
 ne tende pas vers 0 en
ne tende pas vers 0 en 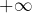
➡ Le premier exemple est facile à trouver. Il suffit de considérer l’intégrale divergente :
![]()
➡ Le second sera moins immédiat, car si ![]() converge et si
converge et si ![]() admet une limite en
admet une limite en ![]() alors cette limite est nécessairement nulle (voir l’exercice n° 2 de cette fiche). Il nous faut donc une application
alors cette limite est nécessairement nulle (voir l’exercice n° 2 de cette fiche). Il nous faut donc une application ![]() ne possédant pas de limite en
ne possédant pas de limite en ![]() Considérons celle-ci :
Considérons celle-ci :
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\int_{1}^{x}\cos\left(t^{2}\right)\thinspace dt & = \left[\frac{\sin\left(u\right)}{2\sqrt{u}}\right]_{1}^{x^{2}}+\int_{1}^{x^{2}}\frac{\sin\left(u\right)}{4u^{3/2}}\thinspace du\\& = \frac{\sin\left(x^{2}\right)}{2x}-\frac{\sin\left(1\right)}{2}+\int_{1}^{x^{2}}\frac{\sin\left(u\right)}{4u^{3/2}}\thinspace du\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8fa5c952b3a0edbca6e12d3fe58c2376_l3.png)
Précisons qu’il est possible de montrer que :
![]()
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
