Challenge 72 : A propos de 2022

  • Auteur/autrice de la publication :
  • Post category:Challenge
icone-challenge-math-OS

Notons C l’ensemble des carrés parfaits :

    \[C=\left\{ a^{2};\thinspace a\in\mathbb{N}\right\}\]

Les premiers éléments de C sont 0,1,4,9,16,\cdots

Posons, pour tout n\in\mathbb{N}^{\star} :

    \[X_{n}=\frac{1}{n}\sum_{k=1}^{n}k^{2}\]

Dans cette vidéo :

on affirme deux choses :

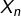  1. Les entiers naturels n pour lesquels X_{n} est entier sont exactement ceux de la forme 6k\pm1.
  2. Si l’on pose :

        \[E=\left\{ n\in\mathbb{N}-\left\{ 0,1\right\} ;\:X_{n}\in C\right\}\]

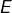    alors le plus petit élément de E est 337.

➣ Sauriez-vous établir le premier point ?

➣ Sauriez-vous montrer que l’ensemble E est infini ?

Une solution est consultable ici

Partager cet article
    
Étiquettes : , , , , , , , , , , , , ,

Cet article a 2 commentaires

  1. J 3 Jan 2022 Répondre

    En me creusant bien la tête, j’arrive à résoudre la question 2 en passant par une équation de Pell-Fermat. Ce n’est pas vraiment au niveau Math-Sup, mais en bonus on peut engendrer simplement tout l’ensemble E.

    As-tu une solution plus raisonnable ?

    1. René Adad 3 Jan 2022 Répondre

      Non, je n’ai pas mieux. C’est de cette façon que j’ai résolu cette question, mais en faisant en sorte de ne pas avoir à connaître grand chose sur les équations diophantiennes en général et sur l’équation de Pell en particulier. En gros, l’identité

          \[ \left(a_{1}^{2}-nb_{1}^{2}\right)\left(a_{2}^{2}-nb_{2}^{2}\right)=\left(a_{1}a_{2}+nb_{1}b_{2}\right)^{2}-n\left(a_{1}b_{2}+b_{1}a_{2}\right)^{2} \]

      permet de prouver que E est infini (pas besoin de prouver qu’on sait engendrer tout E : il suffit d’en engendrer une partie infinie).

Laisser un commentaire