Neuf énoncés d’exercices sur les séries numériques (fiche 02).

Pour tout ![]() on note
on note ![]() le nombre de diviseurs impairs de
le nombre de diviseurs impairs de ![]() Montrer que les séries numériques :
Montrer que les séries numériques :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant1}\frac{d_{n}}{n^{3}}\qquad\sum_{n\geqslant1}\thinspace\frac{\sqrt{n}}{d_{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-34e9f3af2c6c92abd07325cad3003803_l3.png)

Soit ![]() une suite termes positifs. On suppose que la suite
une suite termes positifs. On suppose que la suite ![]() converge vers
converge vers ![]()
Montrer que la série ![]() converge.
converge.
Appliquer ceci pour établir la convergence de la série 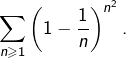

Nature, selon le paramètre ![]() de la série de terme général :
de la série de terme général :
![]()

Nature de la série de terme général :
![]()

Etudier la nature de la série de terme général :
![Rendered by QuickLaTeX.com \[u_{n}=\frac{1}{{\displaystyle \sum_{k=1}^{n}k^{1/k}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17dfbde7debafcaa2413f92b1ee1b8e9_l3.png)

Nature de la série de terme général :
![Rendered by QuickLaTeX.com \[q_{n}=\frac{1}{\sqrt{e}}-\left[\cos\left(\frac{1}{n}\right)\right]^{n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2ba63c659f4d6c0bc8674312c8dff2e_l3.png)

Etant donné un réel ![]() on définit une suite
on définit une suite ![]() par les relations :
par les relations :
![]()

On considère une série convergente ![]() et une suite
et une suite ![]() croissante et majorée.
croissante et majorée.
Montrer que la série ![]() converge.
converge.

Donner un exemple d’une série convergente ![]() telle que la série
telle que la série ![]() diverge.
diverge.
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

