Trois énigmes et un peu de maths

Les énigmes (ou « casse-tête », comme on dit parfois), qu’on se raconte entre amis, reposent parfois sur une astuce de langage et n’ont pas grand chose à voir avec les mathématiques …

Par exemple, on vous dit qu’un train électrique se déplace à 80 km/h, que le vent souffle en sens contraire à 70 km/h et que le taux d’humidité de l’air est de 20% puis on vous demande de déterminer dans quel sens la fumée doit nécessairement se propager.

Lire la solution …

Toutes ces données numériques (vitesses du train et du vent, hygrométrie …) sont là pour vous égarer !!

Lisez bien : il s’agit d’un train électrique ! Donc … pas de fumée.

Voici un exemple d’une nature très différente : votre interlocuteur dépose six allumettes sur la table et vous demande de les agencer de manière à former quatre triangles équilatéraux.

Lire la solution …

Cette question fait partie d’une catégorie d’énigmes dont la résolution impose de « sortir » du contexte apparemment imposé par l’énoncé.

Le fait d’avoir disposé ces allumettes sur une surface plane n’est pas innocent : il induit en nous l’idée que tout doit se passer dans un plan.

Or justement, la solution apparaît si l’on envisage une configuration tridimensionnelle.

Il suffit de former, avec ces six allumettes, un tétraèdre régulier : les quatre faces de celui-ci sont les triangles équilatéraux cherchés.

Le coup des allumettes repose sur un ingrédient purement géométrique. Les trois énigmes qui suivent sont, quant à elles, d’un style plus algébrique. J’aimerais partager avec vous les réflexions qu’elles m’inspirent.

Comme ce sont des énigmes assez connues, il y a de bonnes chances que vous en ayez déjà entendu parler…

1 – L’énigme du deuxième tas

Sur une table de votre salon sont disposées, les unes à côté des autres, 50 pièces de monnaie.

Parmi elles, 20 présentent le côté « pile » et les 30 autres présentent le côté « face ».

Tout ceci se déroule dans une pénombre suffisante pour que vous ne puissiez pas distinguer à vue les « piles » des « faces ». Vous apercevez néanmoins les pièces et vous êtes donc capables de les saisir, une à une, pour les déplacer ou les retourner si le cœur vous en dit.

Ajoutons que vous ne pouvez pas non plus distinguer les « piles des « faces » au toucher.

Maintenant, la question : il s’agit d’isoler un certain nombre de pièces pour former un second tas, de telle sorte que les deux tas contiennent autant de pièces présentant le côté « pile ».

Lire la solution …

Le nombre total de pièces (50) et le nombre de pièces présentant le côté « pile » (20) n’ont pas d’importance particulière. Nous pouvons généraliser sans que cela ne complique aucunement la situation. Notons donc :

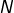$N$ le nombre total de pièces
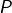$P$ le nombre de pièces présentant le côté « pile »

Prenons $Q$ pièces (avec $1\leqslant Q<N)$ et formons, avec elles, un second tas (le premier tas ne comporte donc plus que $N-Q$ pièces).

Comment nous sommes dans l’obscurité et qu’il est impossible de discerner les « piles » des faces au toucher, nous ne savons évidemment pas, parmi les $Q$ pièces que nous avons sélectionnées, combien présentent le côté « pile ». Disons qu’il y en a $X.$ A présent :

le premier tas comporte 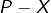$P-X$ pièces côté « pile »,
le second tas comporte 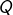$Q$ pièces en tout, dont $X$ côté « pile ».

Il serait miraculeux que l’on ait $P-X=X$ (sans compter que, si $P$ est impair, cela peut difficilement se produire !).

Il faut donc faire quelque chose de plus… mais quoi ?

La bonne idée consiste à retourner les $Q$ pièces formant le second tas. A présent :

le premier tas comporte 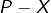$P-X$ pièces côté « pile » (ça n’a pas changé),
le second tas comporte 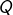$Q$ pièces en tout, dont 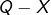$Q-X$ côté « pile ».

Pour que le nombre de pièces côté « pile » soit le même dans les deux tas, il faut donc tout simplement que $Q=P.$

Résumons : on choisit précisément $P$ pièces du tas initial et on les retourne. Point final. On ne peut pas dire qu’il y ait beaucoup de maths là-dedans. Tout au plus la notion de soustraction ! Mais tout de même, il fallait y penser …

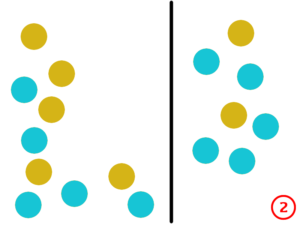
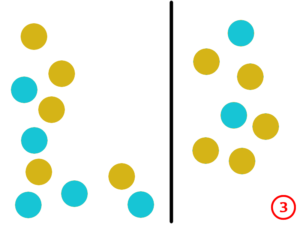
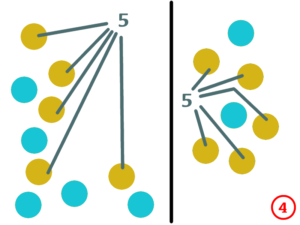
Dans l’illustration ci-dessous, les pièces sont bleues d’un côté et ocres de l’autre.

[1] on démarre avec un tas de 17 pièces, dont 7 présentent leur face ocre,
[2] on isole 7 pièces pour former un petit tas à droite du premier,
[3] on retourne les pièces du petit tas,
[4] on constate qu’il y a maintenant, dans les deux tas, autant de pièces dont la face ocre est visible.

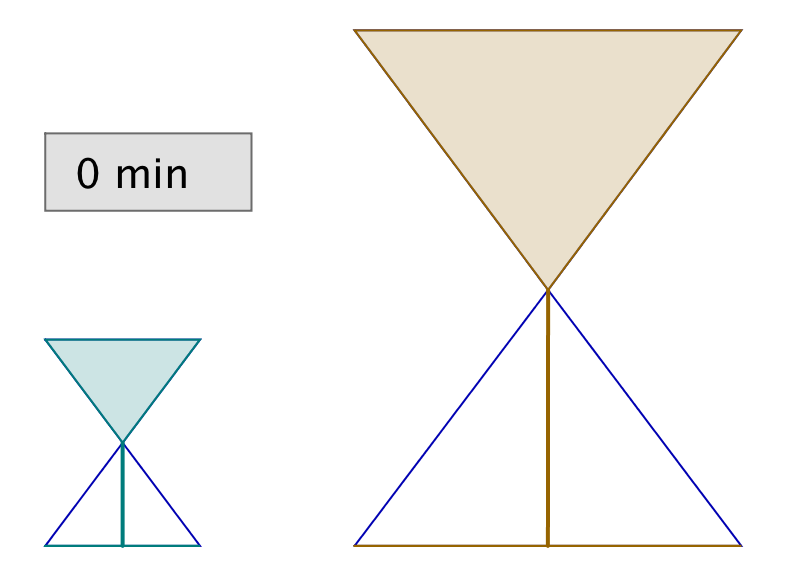
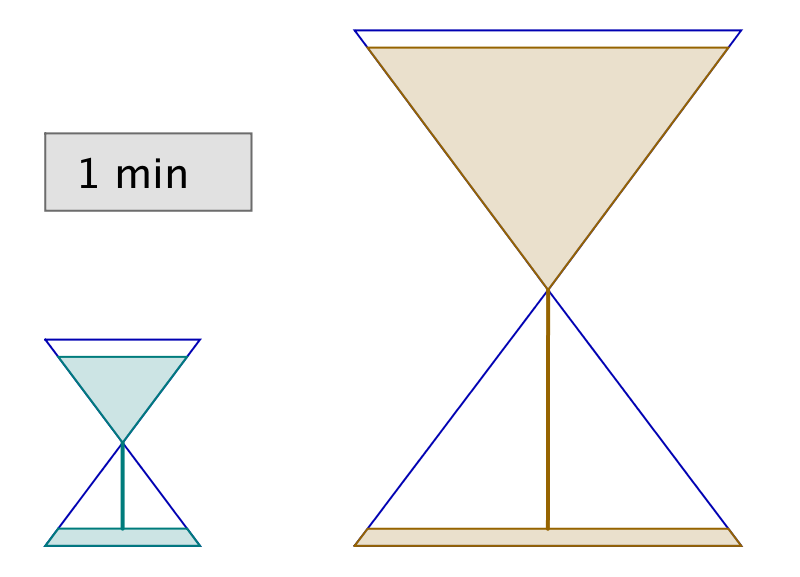
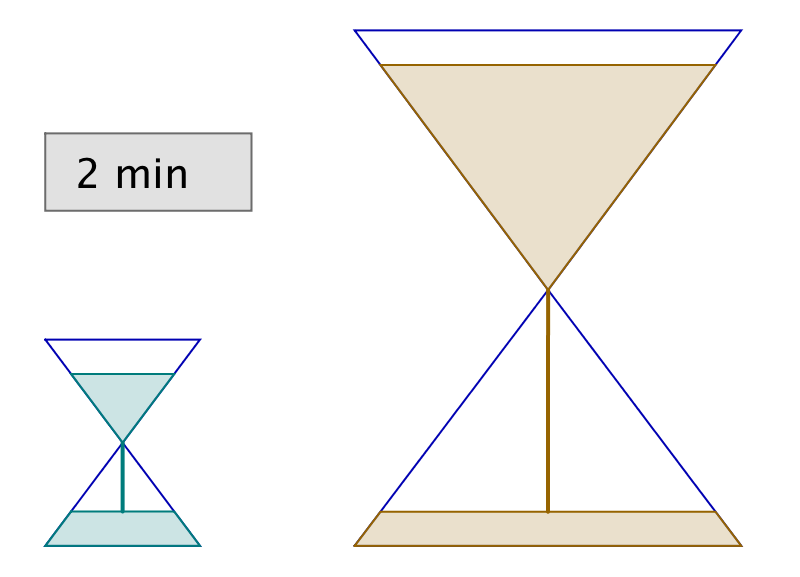
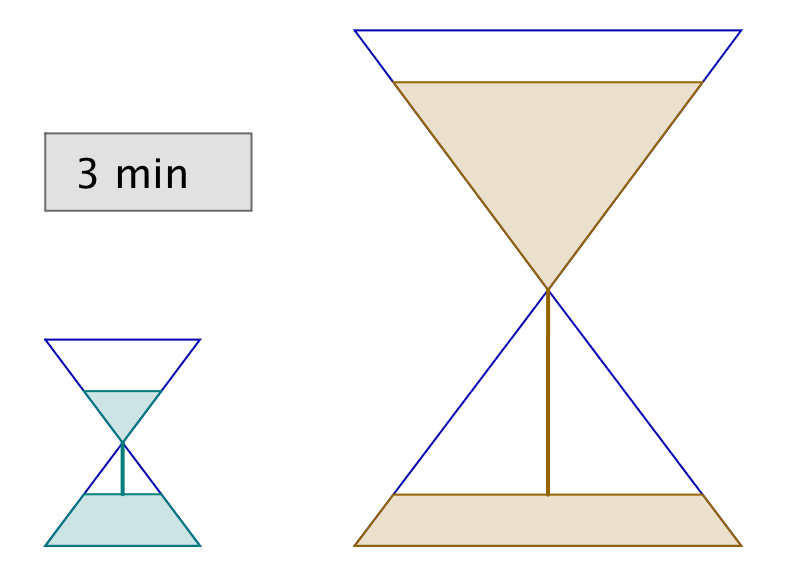
2 – L’énigme des sabliers

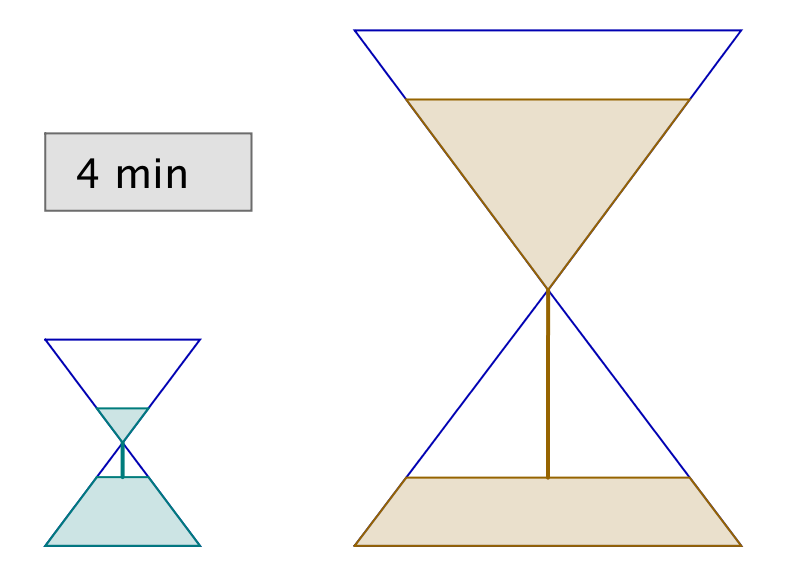
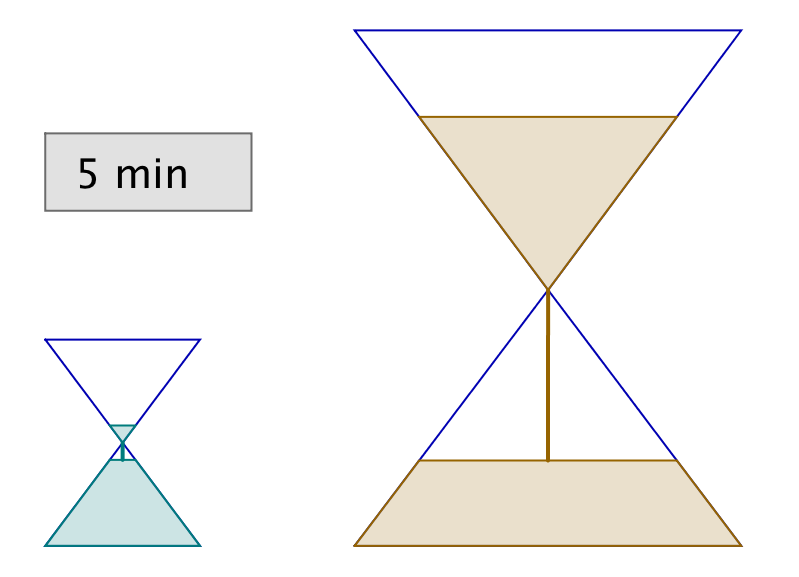
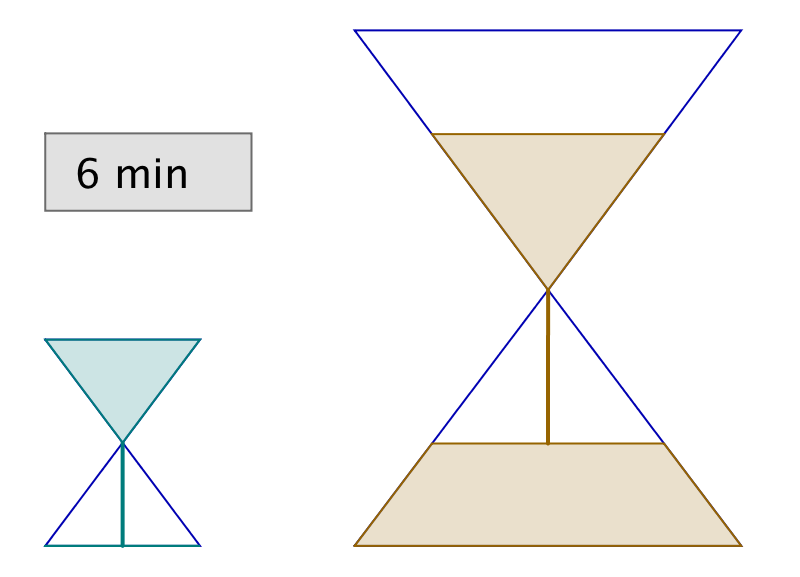
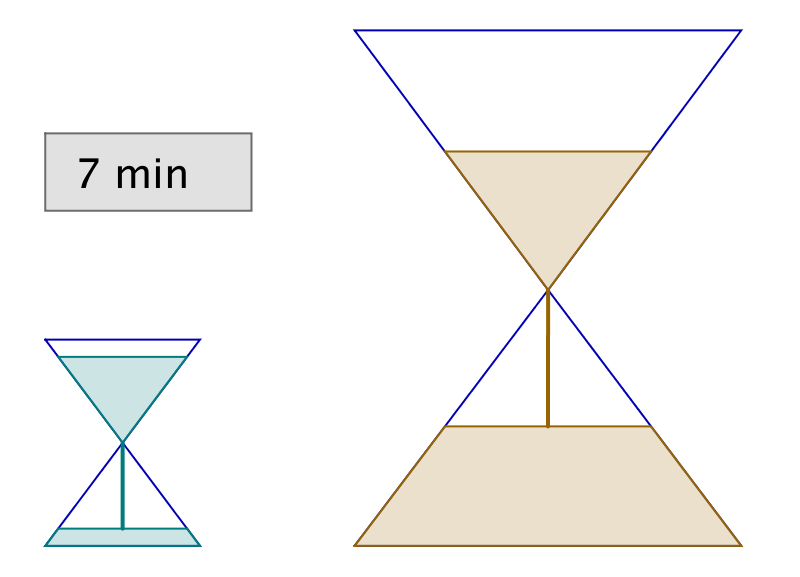
Vous disposez de deux sabliers : l’un se vide en 6 minutes, tandis que l’autre se vide en 15 minutes. A toute fins utiles, précisons que vous ne disposez de rien d’autre pour mesurer le temps (pas de montre ni d’horloge, encore moins de smartphone, etc …) !

Il vous faut chronométrer précisément une durée de 3 minutes.

Est-ce possible et si oui, comment ?

Lire la solution …

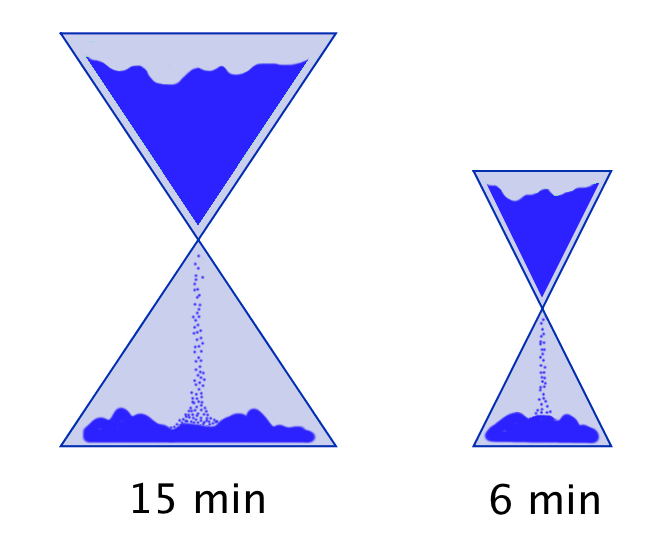
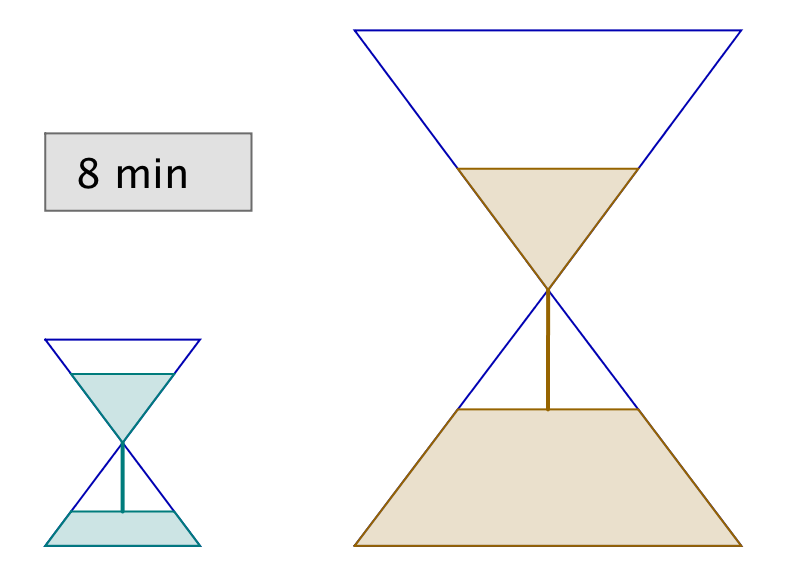
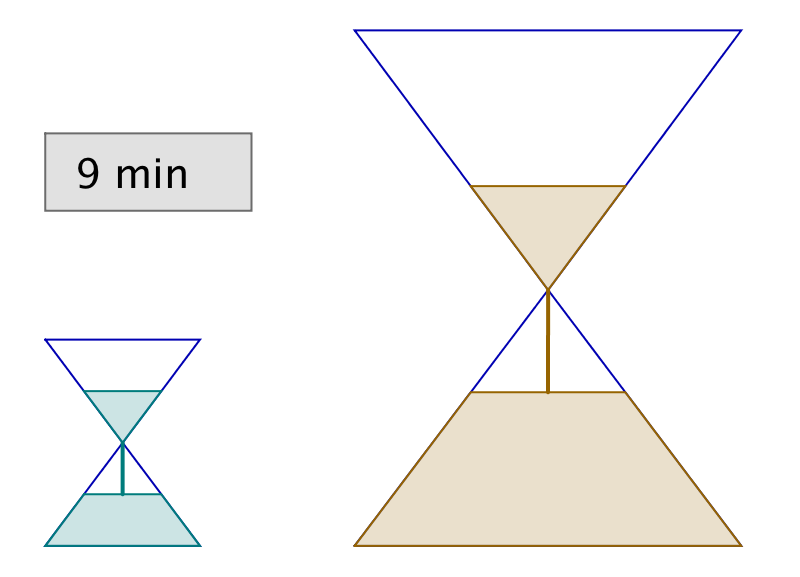
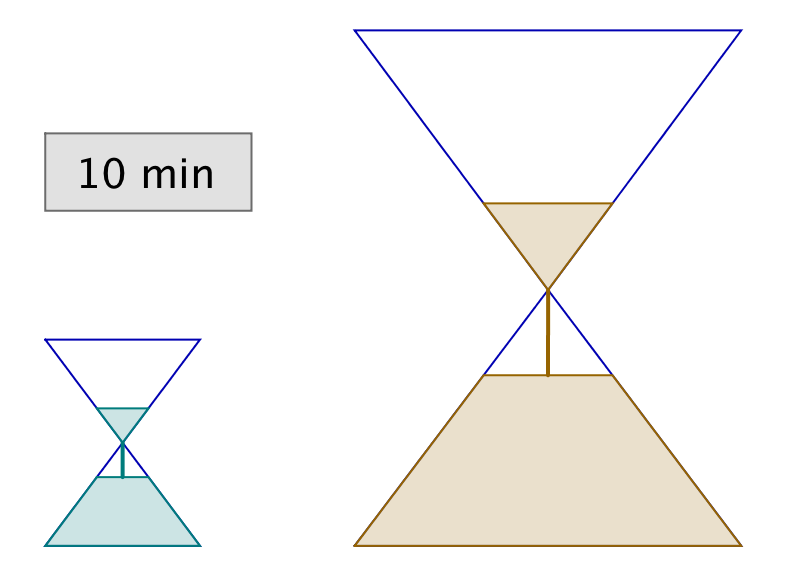
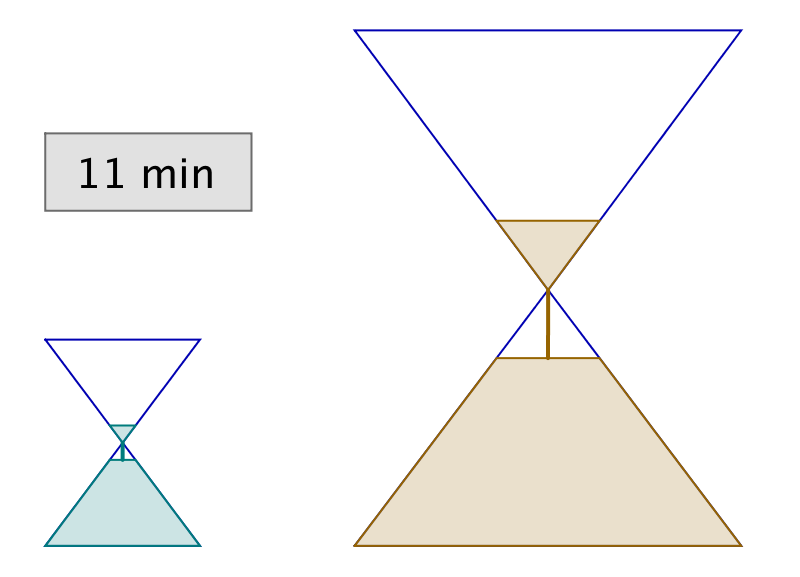
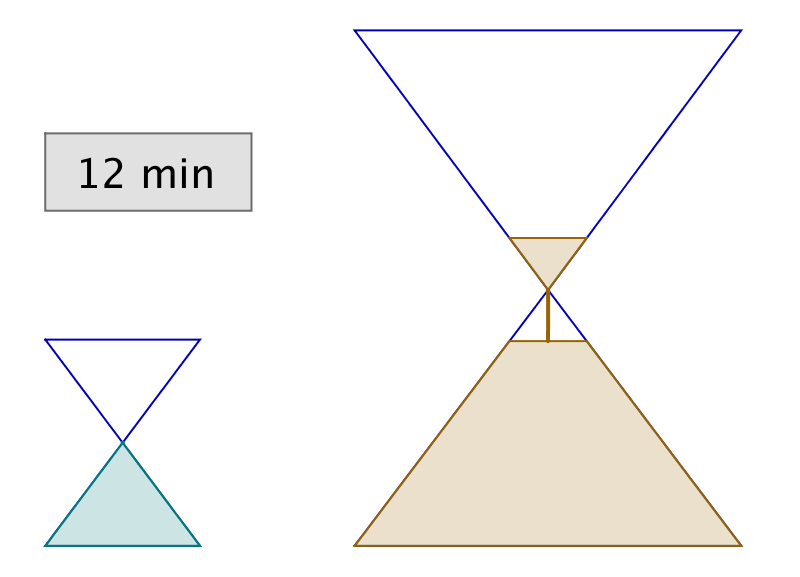
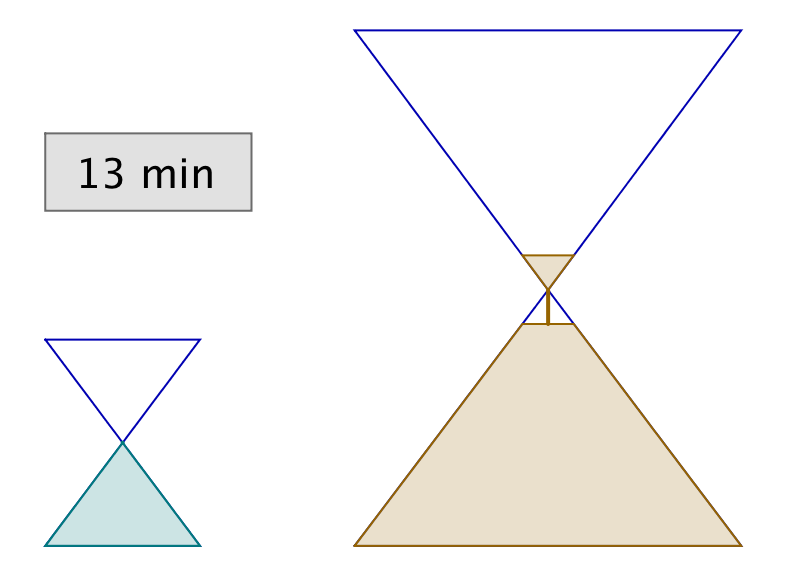
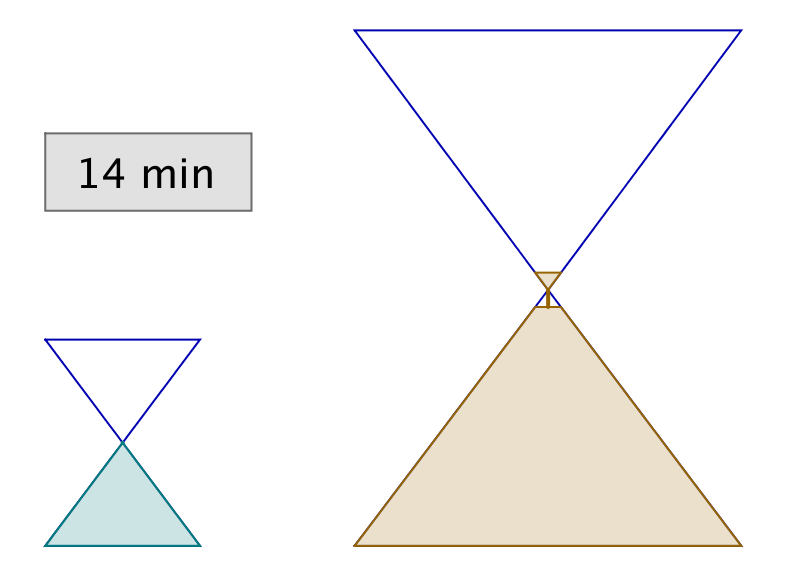
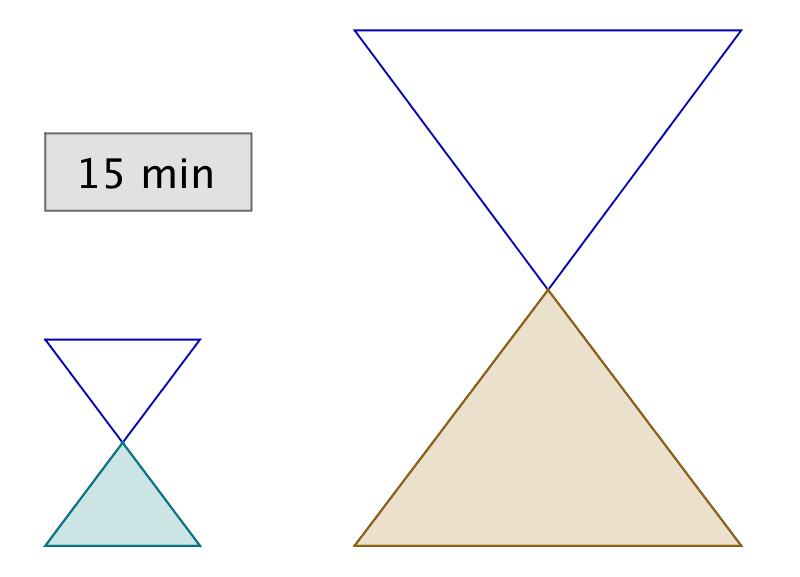
L’astuce consiste à retourner simultanément les deux sabliers. Lorsque le petit se termine, on le retourne et on attend qu’il se termine encore une fois. Il se sera alors écoulé 12 minutes et le grand sablier n’en aura donc plus que pour 3 minutes avant d’être vide.

Dans l’illustration ci-dessous, chaque ligne correspond à un intervalle de temps de 3 minutes. La dernière ligne représente la solution à l’énigme.

Si vous devez faire réchauffer un plat au micro-ondes pendant trois minutes exactement, vous savez désormais comment vous y prendre 🙂

Challenge

Je vous propose la question suivante. Vous disposez de deux sabliers, qui se vident respectivement en 8 minutes pour l’un et 9 minutes pour l’autre. Sauriez-vous mesurer avec cela un intervalle de temps de 5 minutes ?

Si vous trouvez une solution, vous pouvez la partager avec les autres lecteurs du blog. Il vous suffit de me la communiquer en utilisant le formulaire de contact et je la mettrai en ligne 🙂

Cette histoire mérite d’être généralisée …

Etant donnés deux entiers $A,B>0,$ quels sont les entiers positifs que l’on peut former en ajoutant ou en retranchant ces deux-là, un nombre arbitraire de fois ?

La réponse fait intervenir un peu d’arithmétique : si l’on note $D$ le PGCD de $A$ et $B,$ alors les entiers positifs accessibles de cette façon sont exactement les multiples de $D.$ Dans l’exemple ci-dessus, où $A=8$ et $B=9,$ le PGCD est $D=1$ et par conséquent tous les entiers sont accessibles !

Pour $A=6$ et $B=15,$ le PGCD est $D=3.$ Dans ce cas, on peut atteindre exactement les multiples de 3.

Nettement plus compliqué (et plus intéressant) : si l’on interdit les soustractions et que la seule opération autorisée est l’addition, quels sont maintenant les entiers représentables ?

C’est là une question célèbre, que les anglo-saxons ont baptisée « coin’s problem ». C’est le problème des pièces de monnaie (eh oui, encore une histoire de gros sous …), qui peut s’énoncer ainsi :

Coin’s Problem

On dispose de pièces de monnaie de deux types : des pièces de valeur $A$ et des pièces de valeur $B$ ( $A,B$ étant des entiers positifs distincts).

Quels sont les entiers $N$ pouvant s’écrire sous la forme :

$N=xA+yB\qquad\text{avec }x,y\in\mathbb{N}\text{ ?}$

La réponse est connue, mais pas très simple à établir.

On peut notamment montrer que si $A,B$ sont premiers entre eux (ce qui signifie que leur PGCD vaut 1), alors le plus grand entier non représentable est $AB-A-B,$ ce qui signifie que cet entier n’est pas accessible mais que tous ceux qui sont plus grands le sont. Bientôt, j’écrirais sans doute une note à ce sujet, dans la rubrique Articles de niveau supérieur

3 – L’énigme de la pesée

On dépose devant vous cinq sacs : quatre d’entre-eux sont remplis de pièces d’or (toutes identiques) et le cinquième ne contient que des fausses pièces (toutes identiques également).

Les vraies pièces ne peuvent être distinguées des fausses que par leur masse : une vraie pièce d’or pèse 12 grammes, tandis qu’une fausse pèse 10 grammes.

Vous disposez d’une balance électronique munie d’un écran, où s’affiche le poids de l’objet pesé.

Votre mission : déterminer à coup sûr lequel des cinq sacs contient les fausses pièces.

Ce serait évidemment facile si vous pouviez vous servir plusieurs fois de la balance ! Il suffirait d’extraire une pièce de chaque sac, puis de peser ces pièces une à une, jusqu’à ce que la balance affiche 10 grammes.

Oui, mais voilà : vous n’avez droit qu’à une seule pesée !

Lire la solution

Comme pour la première énigme, les valeurs particulières de l’énoncé d’origine n’ont aucune importance.

Disons qu’on dispose de $N$ sacs de pièces d’or et que l’un d’eux seulement, le $I-$ ème, est rempli de fausses pièces.

Le but du jeu : connaître la valeur de cet entier $I.$

On connaît en outre la masse A d’une vraie pièce d’or et la masse $B$ d’une fausse pièce (et bien sûr : $A\neq B$ ).

Il est évident qu’en prenant une pièce dans chaque sac, on formera un échantillon de $N$ pièces dont la masse sera :

$\left(N-1\right)A+B$

Mais comme cette expression ne dépend pas de $I,$ on ne pourra certainement pas localiser le sac de fausses pièces (à moins d’être devin, mais ce n’est pas prévu).

L’idée va être d’introduire une dissymétrie dans la composition de l’échantillon à peser, de telle sorte que la masse de celui-ci dépende injectivement de $I.$

L’adverbe « injectivement » signifie simplement que deux valeurs distinctes de $I$ doivent conduire à des masses distinctes pour l’échantillon. De cette manière, la connaissance de cette masse nous renseignera sans ambiguïté sur la valeur de $I.$

Pour en savoir plus sur les notions d’injection (et de surjection), je vous suggère d’écouter ceci ou même, si nécessaire, de reprendre ces notions à la base avec cette vidéo.

Voici comment nous allons procéder. Prenons :

1 pièce dans le sac n° 1
2 pièces dans le sac n° 2
etc …
N pièces dans le sac n° N

La masse de l’échantillon est cette fois :

$M_{I}=\left[\left(1+2+\cdots+N\right)-I\right]A+IB\qquad\left(\star\right)$

c’est-à-dire :

$M_{I}=\frac{N\left(N+1\right)}{2}A+\left(B-A\right)I\qquad\left(\star\star\right)$

Cette masse $M_I$ dépend injectivement de l’indice $I$ . En effet, si $M_{I}=M_{J},$ alors :

$\frac{N\left(N+1\right)}{2}A+\left(B-A\right)I=\frac{N\left(N+1\right)}{2}A+\left(B-A\right)J$

d’où par différence :

$\left(B-A\right)\left(I-J\right)=0$

Et comme $A\neq B,$ ceci impose $I=J$ .

➭

Si le passage de $\left(\star\right)$ à $\left(\star\star\right)$ vous intrigue, je vous invite à consulter cette vidéo, qui explique en détail le calcul la somme des $n$ premiers entiers.

Et voilà, c’est réglé ! Une seule pesée, bien conçue, permet d’identifier le sac de fausses pièces.

A toutes fins utiles, voici ce que ça donne pour $N=5,$ $A=12$ et $B=10$ :

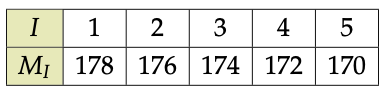
En découvrant le poids indiqué par la balance, on peut aussitôt déterminer la valeur de $I$ et donc localiser le sac de fausses pièces.

Par exemple, si le poids affiché est 176 grammes, alors le sac de fausses pièces est le second.

J’espère que cette article de vulgarisation vous aura intéressé(e).

Merci de me faire part de vos remarques ou de vos questions en commentaire, ou bien en passant par le formulaire de contact.

Partager cet article