Lettre H
HARMONIQUE (série)
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e9e62ff52597157f7ef82d4b070212a_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[H_{2n}-H_{n}=\sum_{k=n+1}^{2n}\frac{1}{k}\geqslant n\times\frac{1}{2n}=\frac{1}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5c8b503212a739bb9f6c18281db015f_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}=\ln\left(2\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-84930d54505da315b6f02e6dc7c6379f_l3.png)
HEINE (théorème de)
Théorème (HEINE)
HYPERPLAN
![]()
![]()
Exemple 1
![Rendered by QuickLaTeX.com \[\left\{ \left(x_{1},\cdots,x_{n}\right)\in\mathbb{K}^{n};\thinspace\sum_{i=1}^{n}a_{i}x_{i}=0\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b5a835308bd79aa4d81f6bd0bcdb17be_l3.png)
Exemple 2
![]()
![]()
- si
 est dimension
est dimension 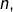 alors tout sous-espace de dimension
alors tout sous-espace de dimension 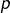 (avec
(avec 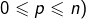 peut être décrit comme l’intersection de
peut être décrit comme l’intersection de  hyperplans de
hyperplans de 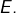
- si
 est de dimension infinie, alors
est de dimension infinie, alors  est isomorphe à l’un quelconque de ses hyperplans.
est isomorphe à l’un quelconque de ses hyperplans. - Si
 est un
est un 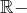 espace vectoriel muni d’un produit scalaire et si
espace vectoriel muni d’un produit scalaire et si 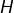 est un hyperplan de
est un hyperplan de  , alors l’orthogonal de
, alors l’orthogonal de 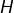 est soit une droite vectorielle (qui est alors le supplémentaire orthogonal de
est soit une droite vectorielle (qui est alors le supplémentaire orthogonal de 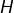 ) soit réduit à
) soit réduit à 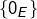 . Voir cet article pour les détails.
. Voir cet article pour les détails. - Si
 est un
est un 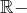 espace vectoriel normé et si
espace vectoriel normé et si 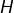 est un hyperplan de
est un hyperplan de  , alors
, alors 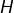 est soit fermé, soit dense dans
est soit fermé, soit dense dans  .
.


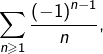 appelée série harmonique alternée. Cette dernière est convergente et sa somme est :
appelée série harmonique alternée. Cette dernière est convergente et sa somme est :