
La propriété à laquelle nous allons nous intéresser ici exprime un fait parfaitement évident.
Elle permet pourtant d’établir des résultats qui, pour certains d’entre-eux, sont loin d’être immédiats !
Il s’agit du « principe des tiroirs », encore appelé « principe de Dirichlet », du nom du mathématicien allemand Peter Gustav Lejeune Dirichlet (1805 – 1859) (voir section 7 du présent article).
Voici son énoncé :
Principe des tiroirs
Si l’on range ![]() objets dans un meuble comportant
objets dans un meuble comportant ![]() tiroirs alors, peu importe la manière dont on procède, l’un au moins des tiroirs contiendra au moins 2 objets.
tiroirs alors, peu importe la manière dont on procède, l’un au moins des tiroirs contiendra au moins 2 objets.

En anglais, la terminologie consacrée est plutôt « principe des nichoirs ». Une version plus « british » de cet énoncé pourrait donc être :
Pigeonhole principle … in french
Si ![]() pigeons sont répartis dans
pigeons sont répartis dans ![]() nichoirs, alors l’un (au moins) des nichoirs accueillera nécessairement deux pigeons (ou davantage)
nichoirs, alors l’un (au moins) des nichoirs accueillera nécessairement deux pigeons (ou davantage)

Dans cette illustration, on voit six pigeons et cinq nichoirs. L’un (au moins) des nichoirs (repéré par un cercle rouge) doit héberger plus d’un pigeon !
Signalons une version améliorée de ce principe.
Considérons une collection de 1000 pièces de monnaie, qu’on décide de classer en 3 catégories : « pièces en or », « pièces en argent » et « autres métaux ».
Si l’on suppose que chacune de ces trois catégories comporte au maximum 333 pièces, alors l’ensemble sera composé d’au plus 3 ![]() 333 = 999 pièces, ce qui est absurde !
333 = 999 pièces, ce qui est absurde !
Par conséquent, l’une de trois catégories doit comporter au moins 334 pièces.
Plus généralement …
Principe des tiroirs généralisé
Si ![]() objets sont répartis en
objets sont répartis en ![]() classes, alors l’une d’elles doit comporter au minimum
classes, alors l’une d’elles doit comporter au minimum ![]() objets.
objets.
Le symbole ![]() désigne la partie entière par excès du réel
désigne la partie entière par excès du réel ![]() c’est-à-dire le plus petit entier supérieur ou égal à
c’est-à-dire le plus petit entier supérieur ou égal à ![]() .
.
On va maintenant présenter quelques applications du principe des tiroirs, en commençant par des exemples simples et en compliquant au fur et à mesure.
1 – Coloriages du plan
Imaginons que nous disposions de deux couleurs pour colorier un plan (un plan de mathématicien, bien sûr !… c’est-à-dire s’étendant indéfiniment dans toutes les directions…). Cela signifie que chaque point du plan se voit attribuer une couleur, parmi deux possibles.
Considérons par ailleurs une distance quelconque ![]() Il existe alors fatalement deux points, situés à la distance
Il existe alors fatalement deux points, situés à la distance ![]() l’un de l’autre, qui sont de la même couleur.
l’un de l’autre, qui sont de la même couleur.
Pour s’en convaincre, il suffit de dessiner dans ce plan un triangle équilatéral de coté ![]() Comme on ne dispose que de deux couleurs, deux des trois sommets (peut-être même les trois !) sont nécessairement de la même couleur… et c’est gagné !
Comme on ne dispose que de deux couleurs, deux des trois sommets (peut-être même les trois !) sont nécessairement de la même couleur… et c’est gagné !

Dans l’illustration ci-dessus, deux des trois sommets du triangle équilatéral sont verts.
De manière analogue, on peut prouver que si l’espace (à trois dimensions) est colorié (de manière arbitraire) à l’aide de trois couleurs, alors pour toute distance ![]() il existera deux points situés à la distance
il existera deux points situés à la distance ![]() l’un de l’autre, qui seront de la même couleur.
l’un de l’autre, qui seront de la même couleur.
Voyez-vous comment l’argument utilisé dans le cas du plan pourrait être adapté ?
Une solution est consultable en fin d’article.
2 – Points à coordonnées entières
Munissons le plan d’un repère (orthonormal ou non, peu importe) et plaçons cinq points à coordonnées entières : l’abscisse et l’ordonnée de chacun d’eux sont des nombres entiers.
Dans le dessin ci-dessous, ces cinq points sont représentés en rouge. Intéressons-nous aux milieux (représentés en bleu) des segments limités par deux points rouges. Les points bleus sont au nombre de ![]() (voir cet article sur les coefficients binomiaux).
(voir cet article sur les coefficients binomiaux).
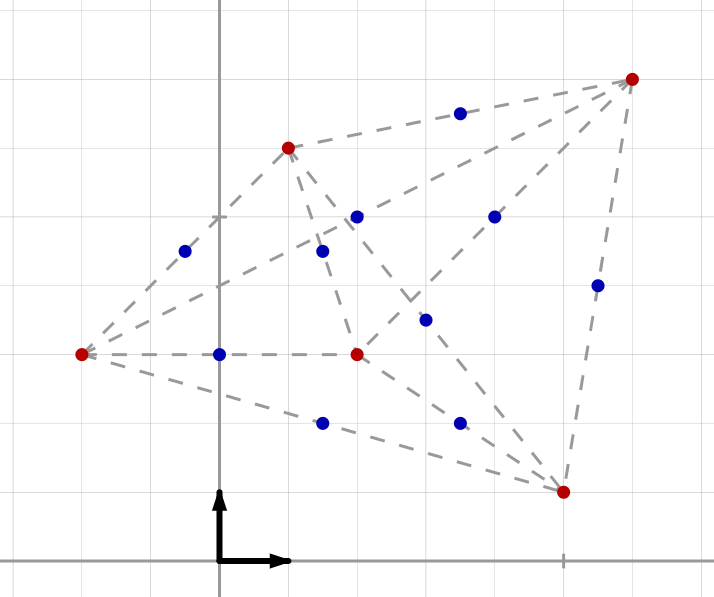
Est-il possible que parmi les dix points bleus, il ne s’en trouve aucun dont les coordonnées soient toutes deux entières ?
Je vous laisse le plaisir d’y réfléchir vous-même : la réponse est détaillée en fin d’article.
3 – Une somme multiple de n
Etant donnés des entiers ![]() quelconques, on va montrer qu’il est toujours possible, en ajoutant certains d’entre eux, d’obtenir un total multiple de
quelconques, on va montrer qu’il est toujours possible, en ajoutant certains d’entre eux, d’obtenir un total multiple de ![]() (la somme doit comporter au moins un terme et l’on s’interdit de prendre plusieurs fois le même).
(la somme doit comporter au moins un terme et l’on s’interdit de prendre plusieurs fois le même).
Nous allons établir ce résultat en appliquant convenablement le principe des tiroirs.
Considérons les entiers :
![]()
Sinon, le reste de la division de chaque ![]() par
par ![]() appartient à
appartient à ![]() Nous avons donc
Nous avons donc ![]() restes et seulement
restes et seulement ![]() valeurs possibles pour ces restes, d’où fatalement deux restes égaux !
valeurs possibles pour ces restes, d’où fatalement deux restes égaux !
Il existe ainsi des indices ![]() tels que
tels que ![]() et
et ![]() multiple de
multiple de ![]() Autrement dit :
Autrement dit : ![]() et le résultat souhaité est établi.
et le résultat souhaité est établi.
Notons que cette preuve est « algorithmique », ce qui signifie qu’elle permet, sans effort supplémentaire, d’écrire un programme qui résout toute instance de ce problème.
Voici, écrit en Python, un tel programme :
def somme_congrue(L):
n = len(L)
s = 0
i = 0
restes = []
encore = True
while encore:
s = s + L[i]
r = s % n
if r == 0:
return L[0 : i+1]
elif restes.count(r) == 0:
restes.append(r)
else:
return L[restes.index(r) + 1 : i + 1]
i += 1Etant donnée une liste L d’entiers, cette fonction calcule les sommes :
L[0], L[0] + L[1], L[0] + L[1] + L[2], etc …
Si l’une d’elles est multiple de n (= la longueur de la liste L), c’est réglé et on s’arrête.
Et si l’une de ces sommes, non multiple de n, est congrue au même reste modulo n qu’une autre somme calculée antérieurement, alors leur différence, qui est une somme du type L[i+1] + … + L[j], convient.
Dans tous les cas, la fonction somme_congrue renvoie une sous-liste (formée de termes consécutifs) de L, dont la somme des termes est multiple de n.
Un exemple :
>>> somme_congrue([17, 3, 12, 7, 10, 3, 5, 1, 5])
[10, 3, 5]On voit bien, en effet, que dans la séquence [17, 3, 12, 7, 10, 3, 5, 1, 5], qui est de longueur 9, la sous-séquence indiquée en rouge totalise 18, qui est un multiple de 9.
4 – Deux exercices à tiroirs 🙂
Chacune des deux questions suivantes met en évidence une particularité des tirages de ![]() entiers parmi
entiers parmi ![]()
Question 1
Choisissons quelques nombres entiers parmi 1, 2, 3, ![]() 10 et regardons s’il est possible d’obtenir un total de 11 en ajoutant deux d’entre-eux.
10 et regardons s’il est possible d’obtenir un total de 11 en ajoutant deux d’entre-eux.
Avec cinq entiers seulement, cela peut ne pas fonctionner, comme on le voit en choisissant 1, 2, 3, 4, 5 (la plus grande somme accessible est 9 = 4 + 5).
Et avec six entiers ? Essayons quelques possibilités, pour voir :
![]()
![]()
![]()
![]()
Mais que faire pour en être absolument certain ? On pourrait poursuivre l’énumération des différentes possibilités … sauf qu’il en existe ![]() (voir l’article sur les propriétés des coefficients binomiaux) ! Et même en effectuant cette tâche fastidieuse, nous n’aurions rien traité de plus qu’un cas particulier : celui où l’on choisit 6 entiers parmi 1, …,10.
(voir l’article sur les propriétés des coefficients binomiaux) ! Et même en effectuant cette tâche fastidieuse, nous n’aurions rien traité de plus qu’un cas particulier : celui où l’on choisit 6 entiers parmi 1, …,10.
Le cas général consiste à montrer qu’en choisissant d’une manière quelconque ![]() entiers parmi
entiers parmi ![]() , il s’en trouvera certainement deux ayant pour somme
, il s’en trouvera certainement deux ayant pour somme ![]() .
.
Il est possible, grâce au principe des tiroirs, de traiter ce cas général de manière élégante.
Voici comment :
Considérons un ensemble ![]() de
de ![]() entiers choisis parmi
entiers choisis parmi ![]()
En formant les ![]() paires d’entiers « complémentaires » :
paires d’entiers « complémentaires » :
![]()
![]()
![]() etc …
etc … ![]()
on voit que deux des ![]() éléments de
éléments de ![]() appartiendront à la même paire.
appartiendront à la même paire.
C’est tout 🙂
Question 2
On peut choisir cinq entiers parmi 1, 2, 3, ![]() 10 de telle sorte qu’aucun d’entre eux n’en divise un autre. C’est en effet le cas si l’on choisit :
10 de telle sorte qu’aucun d’entre eux n’en divise un autre. C’est en effet le cas si l’on choisit :
![]()
![]()
En revanche, si l’on choisit six entiers parmi 1, 2, 3, ![]() 10, alors peu importe la manière de procéder : deux d’entre eux seront tels que le plus petit divise le plus grand.
10, alors peu importe la manière de procéder : deux d’entre eux seront tels que le plus petit divise le plus grand.
Là encore, une solution consisterait à passer en revue les 210 configurations possibles… mais comme on l’a déjà expliqué, ce n’est pas une tâche très passionnante et il vaut mieux se pencher sur le cas général. Nous allons montrer que :
Si ![]() est un entier supérieur ou égal à 1, alors pour tout sous-ensemble
est un entier supérieur ou égal à 1, alors pour tout sous-ensemble ![]() de
de ![]() de cardinal
de cardinal ![]() il existe deux entiers distincts
il existe deux entiers distincts ![]() tels que
tels que ![]()
Pour cela, on commence par écrire chaque élément de ![]() sous la forme
sous la forme ![]() avec
avec ![]() et
et ![]() impair (tout entier naturel non nul peut s’écrire ainsi et d’une seule façon).
impair (tout entier naturel non nul peut s’écrire ainsi et d’une seule façon).
Nécessairement ![]() ce qui donne
ce qui donne ![]() possibilités pour
possibilités pour ![]() (en effet, les entiers impairs
(en effet, les entiers impairs ![]()
![]()
![]() …,
…, ![]() sont au nombre de
sont au nombre de ![]()
Comme ![]() renferme
renferme ![]() éléments, le principe des tiroirs impose que deux d’entre eux soient associés au même
éléments, le principe des tiroirs impose que deux d’entre eux soient associés au même ![]() Ainsi, il existe des entiers
Ainsi, il existe des entiers ![]() tels que
tels que ![]() contienne
contienne ![]() et
et ![]() Et manifestement, le premier est un diviseur du second.
Et manifestement, le premier est un diviseur du second.
Je trouve cette preuve vraiment élégante ! En outre, elle illustre parfaitement la puissance du principe des tiroirs.
Précisons qu’il est possible d’établir le même résultat par une récurrence, mais elle n’est pas commode et cela conduit à quelque chose de nettement moins lumineux :
On prouve par récurrence que l’assertion ![]() suivante est vraie pour tout entier
suivante est vraie pour tout entier ![]() :
:
![]() : « Pour tout
: « Pour tout ![]() vérifiant
vérifiant ![]() il existe
il existe ![]() tel que
tel que ![]() et
et ![]() »
»
D’évidence, ![]() est vraie.
est vraie.
Supposons ![]() vraie pour un certain
vraie pour un certain ![]() et soit
et soit ![]() tel que
tel que ![]()
➡ Si aucun des entiers ![]() et
et ![]() n’appartient à
n’appartient à ![]() alors
alors ![]() et l’hypothèse de récurrence s’applique à
et l’hypothèse de récurrence s’applique à ![]() privé de l’un quelconque de ses éléments.
privé de l’un quelconque de ses éléments.
➡ Si l’un seulement des entiers ![]() et
et ![]() se situe hors de
se situe hors de ![]() alors l’hypothèse de récurrence s’applique au sous-ensemble de
alors l’hypothèse de récurrence s’applique au sous-ensemble de ![]() obtenu en supprimant l’autre.
obtenu en supprimant l’autre.
➡ Supposons à présent que ![]() et
et ![]() appartiennent à
appartiennent à ![]()
- Si
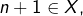 c’est terminé puisque
c’est terminé puisque 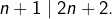
- Sinon, on considére l’ensemble
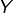 déduit de
déduit de  en remplaçant
en remplaçant 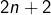 par
par 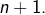 D’après l’hypothèse de récurrence, il existe
D’après l’hypothèse de récurrence, il existe  tels que
tels que 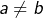 et
et 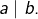
- Si
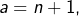 alors nécessairement
alors nécessairement 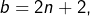 ce qui est exclu. Donc
ce qui est exclu. Donc 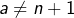 et en particulier
et en particulier 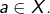
- Si
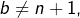 alors
alors 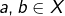 et c’est réglé; et si
et c’est réglé; et si 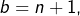 alors a fortiori
alors a fortiori 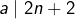 et c’est encore gagné : on a su trouver dans tous les cas deux éléments de
et c’est encore gagné : on a su trouver dans tous les cas deux éléments de 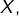 l’un divisant l’autre.
l’un divisant l’autre.
Pour en savoir plus sur les preuves par récurrences, voir cet article introductif et cet autre article, plus approfondi.
5 – Multi-Jackpot
Notons ![]() l’entier dont l’écriture décimale comporte
l’entier dont l’écriture décimale comporte ![]() fois le chiffre 7. Par exemple :
fois le chiffre 7. Par exemple :
![]()
Il existe alors nécessairement un entier ![]() tel que
tel que ![]() soit multiple de
soit multiple de ![]()
En effet, considérons les nombres ![]() et effectuons la division (euclidienne) de chacun d’eux par
et effectuons la division (euclidienne) de chacun d’eux par ![]() Comme chacun des
Comme chacun des ![]() restes est compris entre
restes est compris entre ![]() et
et ![]() (ce qui représente évidemment
(ce qui représente évidemment ![]() possibilités), on voit d’après le principe des tiroirs qu’il doit y avoir deux restes égaux.
possibilités), on voit d’après le principe des tiroirs qu’il doit y avoir deux restes égaux.
Reformulons… il existe nécessairement des entiers ![]() tels que :
tels que :
➡ ![]()
➡ la division de ![]() par
par ![]() et celle de
et celle de ![]() par
par ![]() donnent le même reste.
donnent le même reste.
On parvient ainsi, par différence, à l’égalité :
![]()
![]()
Si la formule ![]() n’est pas claire, l’examen d’un exemple devrait aider :
n’est pas claire, l’examen d’un exemple devrait aider :
![]()
A présent intervient un incontournable théorème d’arithmétique :
Théorème de Gauss
Soient ![]() trois entiers naturels non nuls.
trois entiers naturels non nuls.
Si ![]() divise
divise ![]() et si
et si ![]() est premier avec
est premier avec ![]() alors
alors ![]() divise
divise ![]() .
.
Comme ![]() est premier avec
est premier avec ![]() et donc avec
et donc avec ![]() on voit en appliquant le théorème de Gauss que
on voit en appliquant le théorème de Gauss que ![]() divise
divise ![]() Notre objectif est atteint !
Notre objectif est atteint !
Sauriez-vous trouver, par programme, le plus petit ![]() pour lequel
pour lequel ![]() est divisible par
est divisible par ![]() ? Et par
? Et par ![]() ? Et par
? Et par ![]() ? Réponses en fin d’article.
? Réponses en fin d’article.
6 – Cure de remise en forme
C’est décidé, dès demain, je me remets au sport !
Afin de m’obliger à reprendre de bonnes habitudes, j’ai décidé que pendant ![]() jours consécutifs, je ferai au moins une séance de gym chaque jour. En outre, je m’impose au cours de cette période, un total de
jours consécutifs, je ferai au moins une séance de gym chaque jour. En outre, je m’impose au cours de cette période, un total de ![]() séances.
séances.
Fatalement, il y aura des jours où je devrai faire au moins deux séances ! Mais on peut affirmer quelque chose de moins évident : il y aura nécessairement une suite de jours consécutifs au cours desquels je devrai faire exactement ![]() séances.
séances.
Pour expliquer cela, notons ![]() le nombre de séances de gym effectuées entre le premier et le
le nombre de séances de gym effectuées entre le premier et le ![]() ème jour (inclus). On a donc :
ème jour (inclus). On a donc :
![]()
![]()
Bien sûr, on peut généraliser…
Proposition
Si ![]() sont des entiers tels que :
sont des entiers tels que :
![]()
![]()
![]()
7 – Approximation par des rationnels
Abordons un exemple lié à ce qu’on appelle la théorie des nombres.
Rappelons, pour commencer, qu’un nombre algébrique est par définition un nombre complexe ![]() pour lequel il existe un polynôme non nul à coefficients entiers qui admet
pour lequel il existe un polynôme non nul à coefficients entiers qui admet ![]() parmi ses racines. Le plus petit degré d’un tel polynôme est appelé le degré (d’algébricité) de
parmi ses racines. Le plus petit degré d’un tel polynôme est appelé le degré (d’algébricité) de ![]() Bien entendu, ce degré vaut
Bien entendu, ce degré vaut ![]() lorsque
lorsque ![]() est rationnel.
est rationnel.
Une question importante de théorie des nombres consiste à étudier la précision (ou l’imprécision) avec laquelle un nombre réel peut être approché par des nombres rationnels. Dans ce cadre, un résultat célèbre dû au mathématicien français Joseph Liouville montre que les nombres réels algébriques sont, en un sens, « difficiles à approcher ».

Théorème de Liouville
Si ![]() est algébrique de degré
est algébrique de degré ![]() alors il existe
alors il existe ![]() tel que :
tel que :
![]()
Ce théorème permit à Liouville de donner le premier exemple connu de nombre transcendant. Il pu en effet établir que le nombre réel :
![Rendered by QuickLaTeX.com \[\xi=\sum_{n=0}^{\infty}\frac{1}{10^{n!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f2f37c8dc36c87a4a7eeaaf024e3f54_l3.png)
La première démonstration de ce résultat remarquable a été publiée par Liouville en 1851, dans le Journal de Mathématiques Pures et Appliquées.
Voici un autre résultat, dû à Dirichlet et quasiment contemporain du précédent :
Théorème de Dirichlet
Si ![]() et
et ![]() alors il existe
alors il existe ![]() tel que
tel que
![]()
Corollaire
Si ![]() est irrationnel, alors il existe une infinité de rationnels
est irrationnel, alors il existe une infinité de rationnels ![]() tels que :
tels que :
![]()

C’est pour l’établir que Dirichlet a introduit le Schubfachprinzip, terme allemand qui a été traduit par « principe des tiroirs ».
Passons à la preuve du théorème de Dirichlet :
Preuve (cliquer pour déplier / replier)
Notons ![]() la partie fractionnaire d’un réel t. C’est par définition la différence entre ce nombre et sa partie entière :
la partie fractionnaire d’un réel t. C’est par définition la différence entre ce nombre et sa partie entière :
![]()
Soient ![]() et
et ![]() Comme l’intervalle
Comme l’intervalle ![]() est l’union disjointe des
est l’union disjointe des ![]() « tranches »
« tranches » ![]() pour
pour ![]() le principe des tiroirs assure que deux (au moins) des
le principe des tiroirs assure que deux (au moins) des ![]() réels
réels ![]() tombent dans une même tranche.
tombent dans une même tranche.
Autrement dit, il existe deux entiers ![]() tels que
tels que ![]() ainsi qu’un entier
ainsi qu’un entier ![]() vérifiant :
vérifiant :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\left|x-\frac{p}{q}\right|<\frac{1}{qN}\qquad\text{avec }\left(p,q\right)\in\mathbb{Z}\times\mathbb{N}^{\star}\text{ et }q\leqslant N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-209c6d26463b30fc0e0eedfdc26dc2eb_l3.png)
(![]() )
) ![]()
En un sens, ce théorème de Dirichlet et son corollaire « contrebalancent » le résultat de Liouville : l’un dit en gros que tout irrationnel est approchable à l’ordre au moins 2 par des rationnels, tandis que l’autre exprime l’impossibilité, pour ![]() algébrique de degré
algébrique de degré ![]() d’aller au-delà de l’ordre
d’aller au-delà de l’ordre ![]()
8 – Un théorème de P. Erdös et G. Szekeres
Le célèbre théorème de Bolzano-Weierstrass affirme qu’on peut extraire de toute suite réelle bornée une sous-suite convergente.
Ce résultat peut être démontré très rapidement si l’on connaît le :
Lemme des pics
De toute suite réelle, on peut extraire une sous-suite monotone.
En effet, si une suite réelle est bornée, elle admettra d’après ce lemme une sous-suite monotone et bornée, donc convergente.
On peut donner une preuve directe de ce lemme (voir l’exercice n° 9 de cette fiche), ou bien le voir comme un corollaire d’un important théorème de F. Ramsey :
Théorème (Ramsey)
Pour tout graphe complet infini et pour toute coloration finie de ce graphe, il existe un sous-graphe complet monochrome infini.
Il suffit en effet, étant donnée une suite réelle ![]() de considérer le graphe complet dont les sommets sont les entiers naturels et de le colorier de la façon suivante. L’arête
de considérer le graphe complet dont les sommets sont les entiers naturels et de le colorier de la façon suivante. L’arête ![]() est coloriée en :
est coloriée en :
rouge si ![]()
vert si ![]()
bleu si ![]()
L’existence d’un sous-graphe complet monochrome infini exprime alors l’existence d’une sous-suite strictement monotone ou constante.
Venons-en à l’objet de cette section. En 1935, les mathématiciens hongrois Paul Erdös et Georges Szekeres publièrent ce qu’on pourrait appeler une « version finie » du lemme des pics :
Théorème (Erdös – Szekeres)
Soient ![]() deux entiers naturels non nuls. De toute liste de
deux entiers naturels non nuls. De toute liste de ![]() réels, on peut extraire une sous-liste croissante de longueur
réels, on peut extraire une sous-liste croissante de longueur ![]() ou une sous-liste décroissante de longueur
ou une sous-liste décroissante de longueur ![]()
Dans cet énoncé, le « ou » est inclusif et l’adjectif « (dé)croissante » doit être compris au sens large.
Soit ![]() une liste de réels. Supposons que toute sous-liste croissante de
une liste de réels. Supposons que toute sous-liste croissante de ![]() soit de longueur
soit de longueur ![]() et que toute sous-liste décroissante de
et que toute sous-liste décroissante de ![]() soit de longueur
soit de longueur ![]()
Pour chaque ![]() notons :
notons :
➡ ![]() la longueur maximum d’une sous-liste croissante qui démarre en
la longueur maximum d’une sous-liste croissante qui démarre en ![]()
➡ ![]() la longueur maximum d’une sous-liste décroissante qui démarre en
la longueur maximum d’une sous-liste décroissante qui démarre en ![]()
Par hypothèse ![]() et
et ![]() pour tout
pour tout ![]() , d’où
, d’où ![]() valeurs possibles pour les
valeurs possibles pour les ![]() couples
couples ![]() D’après le principe des tiroirs, il existe deux indices
D’après le principe des tiroirs, il existe deux indices ![]() tels que
tels que ![]() tels que
tels que ![]() Notons
Notons ![]() ce couple. Si
ce couple. Si ![]() alors en préfixant par
alors en préfixant par ![]() une sous-liste croissante de longueur
une sous-liste croissante de longueur ![]() qui démarre en
qui démarre en ![]() on obtient une sous-liste croissante de longueur
on obtient une sous-liste croissante de longueur ![]() qui démarre en
qui démarre en ![]() : c’est impossible ! Et si
: c’est impossible ! Et si ![]() alors en préfixant par
alors en préfixant par ![]() une sous-liste décroissante de longueur
une sous-liste décroissante de longueur ![]() qui démarre en
qui démarre en ![]() on obtient une sous-liste décroissante de longueur
on obtient une sous-liste décroissante de longueur ![]() qui démarre en
qui démarre en ![]() : c’est impossible !
: c’est impossible !
Cette contradiction montre que ![]() possède une sous-liste croissante de longueur
possède une sous-liste croissante de longueur ![]() ou une sous-liste décroissante de longueur
ou une sous-liste décroissante de longueur ![]()

Cette photographie, prise en 1984 à l’université de Newcastle (Australie) montre Georges Szekeres (à droite), son épouse Esther (née Klein) et Paul Erdös (au milieu). Georges et Esther Szekeres furent des mathématiciens de premier plan. Quant à Paul Erdös, on peut dire qu’il fut un mathématicien hors norme.
Esther Szekeres fut notamment à l’origine d’une très jolie question de géométrie combinatoire : étant donnés cinq points du plan en position générale (càd qu’on ne peut pas trouver, parmi eux, trois points alignés), montrer que quatre d’entre eux sont les sommets d’un quadrilatère convexe. Ce problème, résolu par Georges Szekeres, fut dénommé « happy ending problem » par Paul Erdös, car Georges et Esther se marièrent peu de temps après.
Réponses aux questions laissées en suspens
Coloriage
Il suffit de considérer un tétraèdre régulier d’arête d. Vu qu’on ne dispose que de trois couleurs et que le tétraèdre possède quatre sommets, deux au moins des quatre sommets seront de la même couleur.
Points à coordonnées entières
Non, ce n’est pas possible et l’un au moins des dix milieux est nécessairement à coordonnées entières.
En effet, les points du plan qui sont à coordonnées entières peuvent être répartis en quatre catégories, selon la parité de leurs coordonnées :
• Catégorie 1 : abscisse paire et ordonnées paire
• Catégorie 2 : abscisse paire et ordonnées impaire
• Catégorie 3 : abscisse impaire et ordonnées paire
• Catégorie 4 : abscisse impaire et ordonnées impaire
Etant donnés qu’il y a cinq points rouges et quatre catégories, l’une des catégorie comporte (au moins) deux d’entre-eux, d’après le principe des tiroirs. Le milieu de ces deux points est alors à coordonnées entières (car la somme de deux entiers de même parité est paire).
On peut formuler un énoncé analogue dans l’espace : sauriez-vous trouver le nombre minimal ![]() de points (à coordonnées entières) à considérer pour qu’on soit sûr que, parmi les
de points (à coordonnées entières) à considérer pour qu’on soit sûr que, parmi les ![]() milieux, l’un au moins soit à coordonnées entières ?
milieux, l’un au moins soit à coordonnées entières ?
Multi-Jackpot
Avec le langage Python, on peut définir la fonction suivante :
def cherche(d):
if d % 2 == 0 or d % 5 ==0:
print (d, "n'est pas premier avec 10")
return
n = 1
m = 7
while not m % d == 0:
n += 1
m = 10 * m + 7
return nCette fonction renvoie ![]() le plus petit entier
le plus petit entier ![]() pour lequel
pour lequel ![]() (cf. notations de la section 5) est multiple de
(cf. notations de la section 5) est multiple de ![]() (ou bien affiche un message d’erreur si jamais
(ou bien affiche un message d’erreur si jamais ![]() n’est pas premier avec
n’est pas premier avec ![]() On trouve ainsi que :
On trouve ainsi que :
![]()
![]()
![]()
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Je vous en prie, c’est bien le minimum que je puisse faire 😊
Bonsoir,
Merci pour ce très bel article.
J’ai relevé quelques micro-coquilles (sauf erreur de ma part bien sûr!) :
– Partie 4 question 1 : (…) il s’en trouvera certainement deux ayant pour somme « 2n+1 » au lieu de 2n ;
– Partie 7 dans le corollaire qui suit le théorème de Dirichlet : (…) il existe une infinité de « rationnels » au lieu d’irrationnels ;
– Partie 8 dans l’énoncé du théorème de Ramsey : il me semble qu’il est nécessaire d’ajouter que le sous-graphe mentionné est infini.
Puis juste en-dessous, à la deuxième ligne qui suit les cas rouge vert bleu, on peut remplacer « monotone » par « monochrome » et ajouter « infini » ;
– Tout à la fin de l’article, dans l’encadré violet à la fin des réponses, il est peut-être plus clair de renommer les trois quantités. Par exemple D37 à la place de A37, puisque les An sont déjà définis par ailleurs.
Bien à vous.
Un grand merci pour votre lecture attentive. Vous êtes bien aimable de qualifier de « micro-coquilles » les erreurs que vous avez débusquées ! J’ai effectué les mises à jour qui s’imposaient et j’en ai profité pour éliminer encore une erreur qui traînait à la section 5 : la bonne formule (*) est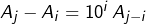 . Comme quoi, on a beau se relire …
. Comme quoi, on a beau se relire …
Je vous suis donc très reconnaissant de m’avoir signalé ces anomalies et je dois dire que c’est un peu navrant qu’elles aient pu rester là près de quatre ans, sans que personne ne les déniche !