
Etant donnés deux nombres réels ![]() strictement positifs, il est facile de prouver que leur moyenne géométrique
strictement positifs, il est facile de prouver que leur moyenne géométrique ![]() est inférieure ou égale à leur moyenne arithmétique
est inférieure ou égale à leur moyenne arithmétique ![]() En effet :
En effet :
![]()
![]()
Remarque
Les puissances avec exposant rationnel (et, en particulier, la notion de racine ![]() ème) sont étudiées à la section 5 de cet article, auquel on pourra se reporter si nécessaire.
ème) sont étudiées à la section 5 de cet article, auquel on pourra se reporter si nécessaire.
Il sera parfois commode de noter, pour ![]() et
et ![]() :
:
![]()
![]()
1 – Preuve par convexité
Ce qui suit suppose connue la notion de fonction convexe.
L’inégalité de Jensen, appliquée à la fonction exponentielle, montre que :
![Rendered by QuickLaTeX.com \[\exp\left(\sum_{i=1}^{n}t_{i}z_{i}\right)\leqslant\sum_{i=1}^{n}t_{i}\thinspace\exp\left(z_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94183a19e37f2482f86a01f06e201744_l3.png)
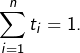
Maintenant, considérons des réels ![]() et choisissons, pour tout
et choisissons, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\exp\left(\dfrac{1}{n}\sum_{i=1}^{n}\ln\left(x_{i}\right)\right)\leqslant\dfrac{1}{n}\sum_{i=1}^{n}\exp\left(\ln\left(x_{i}\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42126d8be06280c69dc5b795da3ef487_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\left(\prod_{i=1}^{n}x_{i}\right)^{1/n}\leqslant\dfrac{1}{n}\sum_{i=1}^{n}x_{i}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d0e1dfc0b0048b4e7abf1468aca06222_l3.png)
2 – Preuve par homogénéité
On procède en deux étapes …
ETAPE 1
On prouve d’abord par récurrence la :
Proposition
Pour tout entier ![]() si
si ![]() sont tels que
sont tels que 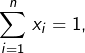 alors :
alors :
![Rendered by QuickLaTeX.com \[\prod_{i=1}^{n}\,x_{i}\leqslant\frac{1}{n^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fb1b0d2845515f9fb15f05500b8940b3_l3.png)
Initialisation (![]() ) – Soient
) – Soient ![]() tels que
tels que ![]() Alors :
Alors :
![]()
![]()
Hérédité – Supposons la propriété vraie au rang ![]() pour un certain
pour un certain ![]() Soient alors
Soient alors ![]() positifs, de somme
positifs, de somme ![]() Il s’agit de montrer que :
Il s’agit de montrer que :
![Rendered by QuickLaTeX.com \[\prod_{i=1}^{n+1}x_{i}\leqslant\dfrac{1}{\left(n+1\right)^{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-16006dd8953327af30f43897bcd9c813_l3.png)
(![]() )
) ![Rendered by QuickLaTeX.com \[\prod_{i=1}^{n+1}\,x_{i}=\left(\prod_{i=1}^{n}\,\frac{x_{i}}{1-x_{n+1}}\right)x_{n+1}\left(1-x_{n+1}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-614b78423c0054371ba2696cebe62e68_l3.png)
(![]() )
) ![Rendered by QuickLaTeX.com \[\prod_{i=1}^{n}\,\frac{x_{i}}{1-x_{n+1}}\leqslant\frac{1}{n^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-871afe6325b29aace25aea905ff6a1ed_l3.png)
![]()
(![]() )
) ![]()
ETAPE 2
Considérons un entier ![]() et des réels
et des réels ![]() Pour montrer que :
Pour montrer que :
![Rendered by QuickLaTeX.com \[\left(\prod_{i=1}^{n}a_{i}\right)^{1/n}\leqslant\dfrac{1}{n}\sum_{i=1}^{n}a_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42a3c6a82272db413605a2d19f882a1a_l3.png)
- Si
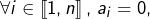 c’est évident.
c’est évident. - Si
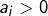 pour au moins un indice
pour au moins un indice 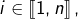 alors en posant
alors en posant 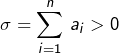 et
et 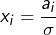 pour tout
pour tout 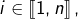 on voit que
on voit que 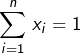 et l’étape 1 s’applique. On obtient :
et l’étape 1 s’applique. On obtient :
c’est-à-dire :![Rendered by QuickLaTeX.com \[\prod_{i=1}^{n}x_{i}\leqslant\dfrac{1}{n^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2798241de2390059b54001dc724e7503_l3.png)
d’où la conclusion, en passant aux racines![Rendered by QuickLaTeX.com \[\prod_{i=1}^{n}a_{i}\leqslant\left(\dfrac{\sigma}{n}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e74d774d9730bdaba8a0cd560c29d31b_l3.png)
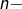 èmes.
èmes.
3 – Preuve par récurrence directe
Remarque
La preuve qui suit fait aussi l’objet de l’exercice n° 9 cette fiche
Pour ![]() l’inégalité
l’inégalité ![]() est connue pour
est connue pour ![]() Supposons que, pour un certain
Supposons que, pour un certain ![]() on ait :
on ait :
![]()
![]()
![]()
(![]() )
) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4 – La preuve de Cauchy
Dans son cours d’analyse algébrique, publié en 1821, Cauchy explique, entre autres, quelles sont les règles usuelles de manipulation des inégalités. Pour ![]() et
et ![]() il prouve que :
il prouve que :
![Rendered by QuickLaTeX.com \[\left(\prod_{i=1}^{n}a_{i}\right)^{1/n}\leqslant\dfrac{1}{n}\sum_{i=1}^{n}a_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42a3c6a82272db413605a2d19f882a1a_l3.png)
![]()
![Rendered by QuickLaTeX.com \[a_{1}\cdots a_{n}S^{2^{k}-n}\leqslant\left(\dfrac{a_{1}+\cdots+a_{n}+\left(2^{k}-n\right)S}{2^{k}}\right)^{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c807504671c1ac50795f01b89798718_l3.png)
![]()
Détail : les cas des puissances de 2
Notons ![]() l’assertion suivante. Quels que soient
l’assertion suivante. Quels que soient ![]() :
:
![Rendered by QuickLaTeX.com \[\left(\prod_{i=1}^{2^{n}}a_{i}\right)^{2^{-n}}\leqslant2^{-n}\sum_{i=1}^{2^{n}}a_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0604c5c395d06db7556b1c17b139fcb3_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}G_{2^{n+1}}\left(a_{1},\cdots,a_{2^{n+1}}\right) & = & \left[G_{2^{n}}\left(a_{1},\cdots,a_{2^{n}}\right)\,G_{2^{n}}\left(a_{2^{n}+1},\cdots,a_{2^{n+1}}\right)\right]^{1/2}\\& \leqslant & \frac{1}{2}\left[G_{2^{n}}\left(a_{1},\cdots,a_{2^{n}}\right)+G_{2^{n}}\left(a_{2^{n}+1},\cdots,a_{2^{n+1}}\right)\right]\\& \leqslant & \frac{1}{2}\left[A_{2^{n}}\left(a_{1},\cdots,a_{2^{n}}\right)+A_{2^{n}}\left(a_{2^{n}+1},\cdots,a_{2^{n+1}}\right)\right]\\& = & A_{2^{n+1}}\left(a_{1},\cdots,a_{2^{n+1}}\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d5f64abbb94b14961483eb96da6a787_l3.png)
5 – Et la moyenne harmonique ?
En dehors des moyennes arithmétique et géométrique, on définit usuellement la moyenne harmonique de ![]() Il s’agit du nombre dont l’inverse est la moyenne arithmétique des inverses. Autrement dit :
Il s’agit du nombre dont l’inverse est la moyenne arithmétique des inverses. Autrement dit :
![Rendered by QuickLaTeX.com \[H_{n}\left(a_{1},\cdots,a_{n}\right)=\dfrac{n}{\dfrac{1}{a_{1}}+\cdots+\dfrac{1}{a_{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cd15be32bc09f5fbc7cb8a024fe7ea59_l3.png)
Proposition
Les moyenne arithmétique, géométrique et harmonique de ![]() vérifient :
vérifient :
![]()
Soit ![]() et soient
et soient ![]() Nous savons (et nous avons prouvé de plusieurs façons) que :
Nous savons (et nous avons prouvé de plusieurs façons) que :
![]()
![Rendered by QuickLaTeX.com \[H_{n}\left(a_{1},\cdots,a_{n}\right)=\dfrac{1}{A_{n}\left(\dfrac{1}{a_{1}},\cdots,\dfrac{1}{a_{n}}\right)}\leqslant\dfrac{1}{G_{n}\left(\dfrac{1}{a_{1}},\cdots,\dfrac{1}{a_{n}}\right)}=G_{n}\left(a_{1},\cdots,a_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9c052c81a6aa914fe513bdfbffb025c9_l3.png)
Signalons une petite amusette au sujet de la moyenne harmonique : un type effectue un trajet aller-retour entre un lieu A et un lieu B. L’aller s’effectue à la vitesse constante ![]() et le retour s’effectue à la vitesse constante
et le retour s’effectue à la vitesse constante ![]() Quelle est, sur l’ensemble du trajet, la vitesse moyenne
Quelle est, sur l’ensemble du trajet, la vitesse moyenne ![]() ?
?
Si vous posez la question autour de vous, il y a des chances pour qu’on vous réponde : ![]()
Et c’est faux ! La réponse correcte est :
![Rendered by QuickLaTeX.com \[\boxed{v=\dfrac{2}{\dfrac{1}{v_{a}}+\dfrac{1}{v_{r}}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-176a618f8016352326812ffba5b3be09_l3.png)
Explication …
Notons ![]() et
et ![]() les temps mis pour effectuer respectivement l’aller et le retour. En notant
les temps mis pour effectuer respectivement l’aller et le retour. En notant ![]() la distance entre A et B, on voit que :
la distance entre A et B, on voit que :
![Rendered by QuickLaTeX.com \[v=\dfrac{2d}{t_{a}+t_{r}}=\dfrac{2d}{\dfrac{d}{v_{a}}+\dfrac{d}{v_{r}}}=\dfrac{2}{\dfrac{1}{v_{a}}+\dfrac{1}{v_{r}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-22d1be15846db1adcbd28487afe8863e_l3.png)
6 – Un petit exo
Etant donnés quatre nombres réels positifs ![]() tels que
tels que ![]() on demande de montrer que :
on demande de montrer que :
![]()
Voici deux façons de traiter cette question …
Solution 1
On sait que, pour tout ![]() :
:
![]()
Par ailleurs, ![]() et
et ![]() d’où
d’où
![]()
![]()
Solution 2
On applique l’IGA :
![]()
7 – Application : l’inégalité de Carleman
On doit au mathématicien suédois Torsten Carleman (1892 – 1949) le résultat suivant :
Théorème
Pour toute série convergente à termes strictement positifs ![]() , la série de terme général
, la série de terme général ![]() converge et :
converge et :
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\left(a_{1}\cdots a_{n}\right)^{1/n}\leqslant e\thinspace\sum_{n=1}^{\infty}a_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eef1c6206b03372e0585183c2b05b6cd_l3.png)

Jolie majoration ! Et il n’est même pas évident que la série apparaissant au membre de gauche soit convergente … En effet, une idée naturelle pour justifier cette convergence serait d’invoquer le principe de comparaison pour les séries à termes positifs :
![]()
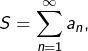 le membre de droite est équivalent à
le membre de droite est équivalent à On notera ![]() Considérons une suite
Considérons une suite ![]() à termes strictement positifs. Pour tout
à termes strictement positifs. Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ G_{n}=\frac{{\displaystyle \left[\prod_{k=1}^{n}\,t_{k}\,a_{k}\right]^{1/n}}}{{\displaystyle \left[\prod_{k=1}^{n}\,t_{k}\right]^{1/n}}}\leqslant\left[\prod_{k=1}^{n}\,t_{k}\right]^{-1/n}\,\frac{1}{n}\,\sum_{k=1}^{n}\,t_{k}\,a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8eced07f90c010d69dda3850c6c5356_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\,G_{k}\leqslant\sum_{k=1}^{n}\,\left(\left[\prod_{i=1}^{k}\,t_{i}\right]^{-1/k}\,\frac{1}{k}\,\sum_{j=1}^{k}\,t_{j}\,a_{j}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b48db3b81b91707278dd02293e586e3b_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\,G_{k}\leqslant\sum_{j=1}^{n}\,\left(t_{j}\,a_{j}\,\sum_{k=j}^{n}\,\frac{1}{k}\left[\prod_{i=1}^{k}\,t_{i}\right]^{-1/k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-41c3ac1e301391cd2e42be5ed4e07f7b_l3.png)
On peut les choisir de telle sorte que :
![Rendered by QuickLaTeX.com \[\forall k\in\mathbb{N}^{\star},\,\left[\prod_{i=1}^{k}\,t_{i}\right]^{-1/k}=\frac{1}{k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d00b4115b359982795544026e313491d_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\,G_{k}\leqslant\sum_{j=1}^{n}\,\left(t_{j}\,a_{j}\,\sum_{k=j}^{n}\,\frac{1}{k\left(k+1\right)}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5b46dc551a460c0e2398e2ecb3e1bbf2_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=j}^{n}\,\frac{1}{k\left(k+1\right)}=\sum_{k=j}^{n}\left(\dfrac{1}{k}-\dfrac{1}{k+1}\right)=\frac{1}{j}-\frac{1}{n+1}<\frac{1}{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2a5fc7a4654d53f70afcb917a3b4593_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\,G_{k}\leqslant\sum_{j=1}^{n}\,\frac{t_{j}}{j}\,a_{j}=\sum_{j=1}^{n}\,\left(1+\frac{1}{j}\right)^{j}\,a_{j}<e\,\sum_{j=1}^{n}\,a_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59dba4cc18ebfb42a12dd4f8ba25d1c1_l3.png)
Remarque
En fait l’inégalité de Carleman est stricte. En effet : reprenons au ralenti ce qui vient de se passer …
La majoration précédente prouve que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}G_{k}\leqslant e\thinspace\sum_{k=1}^{\infty}a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8b1b49fd873b6ed6990b6435560fc411_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}G_{k}\leqslant\sum_{k=1}^{n}\left(1+\dfrac{1}{k}\right)^{k}a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4ca351bdf9392887753c9949bd7120c2_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{\infty}G_{k}\leqslant\sum_{k=1}^{\infty}\left(1+\dfrac{1}{k}\right)^{k}a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-31452ef2ebe4cc095b788fe9d98f07be_l3.png)
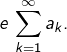
Terminons avec l’optimalité du facteur ![]() Pour cela, considérons, pour tout
Pour cela, considérons, pour tout ![]() la série (harmonique tronquée) de terme général :
la série (harmonique tronquée) de terme général :
![Rendered by QuickLaTeX.com \[a_{n}=\left\{ \begin{array}{ccc}{\displaystyle \frac{1}{n}} & \textrm{si} & 1\leqslant n\leqslant N\\\\0 & \textrm{si} & n>N\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4110e4175a8bd651412639c551cab3c_l3.png)
![Rendered by QuickLaTeX.com \[g_{n}=\left(\prod_{k=1}^{n}\,a_{k}\right)^{1/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e26b4e425e9f3289a076907f2d9583f5_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\,g_{n}=\sum_{n=1}^{N}\,g_{n}\sim\sum_{n=1}^{N}\,\frac{e}{n}\sim e\ln\left(N\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-569c5aa6f0e87eac153c3fa10ab57577_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{n=1}^{\infty}\,a_{n}=\sum_{n=1}^{N}\,\frac{1}{n}\sim\ln\left(n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd41953b608cd027b6b6fbc91b7f8a10_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{N\rightarrow+\infty}\frac{{\displaystyle \sum_{n=1}^{\infty}\,g_{n}}}{{\displaystyle \sum_{n=1}^{\infty}\,a_{n}}}=e\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-345dc6e618a56283dabd58e223765a8c_l3.png)
Si cet article vous a plu, merci de laisser un petit commentaire 🙂
Précisons que le sujet est très loin d’avoir été épuisé. On pourrait par exemple parler de la moyenne arithmético-géométrique ![]() de deux réels
de deux réels ![]() Il s’agit de la limite commune des suites
Il s’agit de la limite commune des suites ![]() et
et ![]() définies par :
définies par :
![]()
![]()

(En revanche pas évidente à trouver sans indication l’inégalité de Carleman 😊 !)
Bonjour Monsieur,
Merci pour ce bel article 😊
Je trouve la preuve de Cauchy agréable, car élégante et donnant l’impression qu’elle peut se trouver seul, en un temps raisonnable, même après avoir oublié beaucoup de notions !
Dans la partie 3 après « Nécessairement : » c’est peut-être ai < A < aj à la place de aiA.
Dans la partie 7, à la fin de l’encadré bleu Remarque, le strictement s’affiche dans son code latex !
Bonne soirée à vous,
Fabrice
Merci beaucoup Fabrice, une fois de plus, pour votre retour.
J’ai mis à jour le texte de l’article.