
Si vous êtes en terminale et que vous envisagez des études scientifiques avec une bonne dose de mathématiques, je vous conseille de vous intéresser de près à ce qui suit.
Le thème abordé (construction rigoureuse des puissances d’exposant quelconque et de la fonction exponentielle) est en effet quasiment inexploré au lycée (en tous cas, pas avec ce niveau de détail) mais joue, en revanche, un rôle-clef en analyse réelle (étude des suites et des fonctions, calcul différentiel et intégral, etc …).
Cet article a donc été placé dans la catégorie Articles de niveau Lycée bien qu’il demeure, par certains côtés, d’un niveau plus avancé. En cas de difficulté, n’hésitez pas à poster vos questions ou remarques en commentaires ou bien en passant par le formulaire de contact.
– Qu’est-ce que l’exponentielle de base ![]() (pour
(pour ![]() fixé) ?
fixé) ?
– Facile ! C’est la fonction ![]()
Si cette définition vous paraît satisfaisante, alors il se peut que certains points — et non des moindres — vous aient échappé.
En effet, le sens de cette écriture est tout sauf tout clair !
A un niveau élémentaire, l’expression ![]() désigne :
désigne :
➡ le produit de ![]() facteurs égaux à
facteurs égaux à ![]() si
si ![]() est un entier strictement positif,
est un entier strictement positif,
➡ le réel ![]() si
si ![]() est un entier strictement négatif (ce qui nous ramène au point ci-dessus),
est un entier strictement négatif (ce qui nous ramène au point ci-dessus),
➡ 1 par convention si ![]()

Mais que pourrait bien signifier, par exemple, le produit de 3,14 facteurs égaux à ![]() ?
?
Et le produit de ![]() facteurs ?
facteurs ?
On voit bien que pour ![]() non entier, le sens de l’écriture
non entier, le sens de l’écriture ![]() doit d’être précisé. C’est là le principal but de cet article et il existe plusieurs façons d’y parvenir.
doit d’être précisé. C’est là le principal but de cet article et il existe plusieurs façons d’y parvenir.
La trajectoire adoptée ici repose sur la construction préalable du logarithme népérien.
1 – Logarithme népérien
Etant donné un entier ![]() il est connu que la dérivée de l’application
il est connu que la dérivée de l’application
![]()
![]()
![]()
Devrait-on en déduire que l’application ![]() ne possèderait pas de primitives ?
ne possèderait pas de primitives ?
Pas vraiment …
Théorème (condition suffisante d’existence de primitives)
Si ![]() est un intervalle (non trivial), alors toute application continue de
est un intervalle (non trivial), alors toute application continue de ![]() dans
dans ![]() possède des primitives.
possède des primitives.
Il est donc licite d’adopter la définition suivante :
Définition 1
On appelle logarithme népérien (notation ![]() la primitive de
la primitive de
![]()
Pour le choix de la terminologie, voir section 2.
Vu que ![]() est strictement positive, on voit que
est strictement positive, on voit que ![]() est strictement croissante. Puis, comme
est strictement croissante. Puis, comme ![]() alors
alors ![]() pour tout
pour tout ![]() et
et ![]() pour tout
pour tout ![]()
La propriété la plus importante de ![]() est sans doute :
est sans doute :
Théorème (équation fonctionnelle du logarithme)
Pour tout couple ![]() de réels strictement positifs :
de réels strictement positifs :
![]()
Preuve (cliquer pour déplier / replier)
Fixons arbitrairement un réel ![]() L’application :
L’application :
![]()
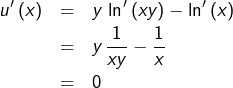
donc
Étudions maintenant le comportement du logarithme népérien au voisinage de 0 et de ![]()
Proposition 1
Les limites de ![]() aux bornes de son intervalle de définition sont :
aux bornes de son intervalle de définition sont :
![]()
Preuve (cliquer pour déplier / replier)
Selon le théorème de la limite monotone, toute application croissante de ![]() dans
dans ![]() possède en
possède en ![]() une limite finie ou infinie.
une limite finie ou infinie.
Dans le cas de ![]() supposons cette limite finie et notons-la
supposons cette limite finie et notons-la ![]() On peut alors passer à la limite dans l’égalité :
On peut alors passer à la limite dans l’égalité :
![]()
ce qui donne
Mais ceci est absurde car
croissante. Par conséquent :
({1) ![]()
![]()
![]()
Il en résulte, d’après
que :
![]()
Grâce au théorème des valeurs intermédiaires, on voit maintenant que ![]() est surjective. Par ailleurs,
est surjective. Par ailleurs, ![]() est injective puisque strictement croissante. En conséquence :
est injective puisque strictement croissante. En conséquence :
Corollaire
Le logarithme népérien est une bijection de ![]() vers
vers ![]()
Il est temps de conclure cette première partie en définissant la fonction exponentielle :
Définition 2
La bijection réciproque de ![]() est appelée exponentielle népérienne (ou simplement : exponentielle).
est appelée exponentielle népérienne (ou simplement : exponentielle).
On la note : ![]()
Peut-être vous attendiez-vous à la notation ![]() plutôt que
plutôt que ![]() … ?
… ?
On y viendra un peu plus bas, mais patience … car il faudra d’abord expliquer ce qui justifie cette écriture et aussi préciser qui est ce nombre ![]() qui n’a jusqu’ici pas été défini.
qui n’a jusqu’ici pas été défini.
2 – Parenthèse historique
L’adjectif népérien trouve son origine dans le patronyme Napier, dont l’orthographe a été francisée en Neper.
Ce qui suit est librement adapté de Wikipedia :
En 1614, le mathématicien écossais John NAPIER (1550-1617) publie son traité Mirifici Logarithmorum Canonis Descriptio. Il ne songe pas qu’il est en train de créer de nouvelles fonctions, mais seulement des tables de correspondances (logos : rapport, relation; arithmos : nombre) entre deux séries de valeurs possédant la propriété suivante : à un produit dans une colonne, correspond une somme dans l’autre.
Ces tables de correspondances ont été initialement créées pour simplifier les calculs trigonométriques apparaissant en astronomie et furent utilisées quelques années plus tard par Kepler.
La notation Log, comme abréviation de logarithme, apparaît en 1616 dans une traduction anglaise de l’œuvre de Neper.

En 1619, apparaît à titre posthume Mirifici Logarithmorum Canonis Constructio, où Neper explique comment construire une table logarithmique.
Son travail est poursuivi par le mathématicien anglais Henry BRIGGS (1560 – 1630) qui publie en 1624 une table de logarithmes décimaux
(Arithmetica logarithmica) et précise comment l’utiliser pour calculer des sinus, retrouver des angles de tangentes … Le logarithme décimal est parfois appelé logarithme de Briggs en son honneur.
La même année, Johann KEPLER publie Chilias logarithmorum, table de logarithmes construite en utilisant un procédé géométrique. La table de Briggs présente les logarithmes à 14 chiffres des nombres compris entre 1 et 20000 et entre 90000 et 100000. Son travail est repris par Ezechiel de Decker et Adriaan Vlacq qui publient en 1627 une table de logarithmes complète.
En 1647, lorsque Grégoire de Saint-Vincent travaille sur la quadrature de l’hyperbole, il met en évidence une fonction : la primitive de ![]() qui s’annule en 1. Mais c’est seulement Huygens qui observe en 1661 qu’il s’agit d’un logarithme particulier : le logarithme naturel.
qui s’annule en 1. Mais c’est seulement Huygens qui observe en 1661 qu’il s’agit d’un logarithme particulier : le logarithme naturel.
La notion de fonction, la correspondance entre les fonctions exponentielles et les fonctions logarithmes n’apparaissent que plus tardivement, après le travail de Gottfried Wilhelm LEIBNIZ (1646-1716) sur la notion de fonction (fin du XVIIème siècle).
Il y a de cela quelques temps, j’ai découvert dans un vieux livre (Memoirs of John Napier of Merchiston par Mark Napier, édité à Londres en 1834) l’extrait suivant, dans lequel l’auteur cite l’un de ses ancêtres (Sir Archibald Napier, le père de John Neper). Ce dernier explique quelle est, selon lui, l’étymologie du patronyme Napier :
One of the ancient Earls of Lennox in Scotland had issue three sons; the eldest, that succeeded him to the Earldom of Lennox; the second, whose name was Donald; and the third, named Gilchrist. The then King of Scots having wars, did convocate his lieges to battle, amongst whom that was commanded was the Earl of Lennox, who, keeping his eldest son at home, sent his two sons to serve for him with the forces that were under his command. This battle went hard with the Scots; for the enemy pressing furiously upon them, forced them to lose ground until it came to flat running away, which being perceived by Donald, he pulled his father’s standard from the bearer thereof, and valiantly encountering the foe, being well followed by the Earl of Lennox’s men, he repulsed the enemy and changed the fortune of the day, whereby a great victory was got. After the battle, as the manner is, every one drawing and setting forth his own acts, the king said unto them, ye have all done valiantly, but there is one amongst you who hath Na-Peer ; and calling Donald into his presence, commanded him, in regard of his worthy service and in augmentation of his honour, to change his name from Lennox to Napier, and gave him the lands of Gosford and lands in Fife, and made him his own servant, which discourse is confirmed by evidences of mine wherein we are called Lennox alias Napier.
Et voici une traduction :
Un des anciens comtes de Lennox en Écosse avait trois fils; l’aîné, qui lui succéda et prit le titre de Comte de Lennox; le second, qui s’appelait Donald; et le troisième, du nom de Gilchrist. Le roi des Écossais de l’époque étant en guerre, convoqua ses vassaux à la bataille, parmi lesquels le Comte de Lennox, qui, préférant garder son fils aîné à la maison, envoya ses deux (autres) fils servir à sa place, avec les bataillons qui étaient sous son commandement. Cette bataille fut difficile pour les Écossais; car l’ennemi, les pressant avec fureur, les força à perdre du terrain jusqu’à ce qu’ils décidèrent tout simplement de s’enfuir, ce qui fut perçu par Donald. Il prit l’étendard de son père au soldat qui le portait, et alla vaillamment à la rencontre de l’ennemi, suivi par les hommes du Comte de Lennox. Il réussit à repousser l’ennemi et par là-même, la fortune du jour, par laquelle une grande victoire fut obtenue. Après la bataille, selon la tradition, chacun exposa en détail ses propres actes de bravoure et le roi leur dit : « Vous avez tous combattu vaillamment, mais il y en a un parmi vous qui a « Na-Peer » (qui n’a pas son égal) et appelant Donald à se présenter devant lui, lui ordonna, en reconnaissance de son service et pour que son honneur soit connu de tous, de changer son nom de Lennox à Napier, et lui donna les terres de Gosford et les terres à Fife, et en fit son propre serviteur. Tout ceci est confirmé par le fait que nous nous appelons Lennox alias Napier.
Fin de la parenthèse historique … revenons à notre sujet.
3 – Exponentielle népérienne
Rappelons le résultat général suivant :
Théorème (dérivabilité d’une bijection réciproque)
Si ![]() sont deux intervalles non triviaux et
sont deux intervalles non triviaux et ![]() une bijection dérivable, dont la dérivée ne s’annule pas, alors sa réciproque
une bijection dérivable, dont la dérivée ne s’annule pas, alors sa réciproque ![]() est aussi dérivable et de plus :
est aussi dérivable et de plus :
![]()
Comme ![]() est une bijection dérivable et comme
est une bijection dérivable et comme ![]() ce théorème montre que
ce théorème montre que ![]() est dérivable et que, pour tout
est dérivable et que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\exp'\left(x\right) = \frac{1}{\ln'\left(\exp\left(x\right)\right)}= \frac{1}{\left(\frac{1}{\exp\left(x\right)}\right)} = \exp\left(x\right) \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-05a824abfdbb4bd9e1ea39a90a0dee85_l3.png)
Proposition 2
L’application ![]() est dérivable et :
est dérivable et :
![]()
Vu que le logarithme népérien transforme les produits en sommes, on obtient aussitôt :
Proposition 3
Pour tout couple ![]() de réels :
de réels :
![]()
Preuve (cliquer pour déplier / replier)
Les logarithmes des deux membres sont égaux; en effet :
![]()
![]()
On conclut en invoquant l’injectivité du logarithme.
Nous sommes maintenant à pied d’œuvre pour faire émerger la notation ![]()
4 – Notation  : première approche
: première approche
Proposition 4
Si ![]() alors pour tout
alors pour tout ![]() :
:
![]()
Preuve (cliquer pour déplier / replier)
Le réel ![]() étant fixé, commençons par traiter le cas
étant fixé, commençons par traiter le cas ![]() en procédant par récurrence.
en procédant par récurrence.
L’égalité est vraie au rang 0 puisque ![]()
Supposons-la vraie pour un certain ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \begin{eqnarray*} \exp\left(\left(n+1\right)x\right) & = & \exp\left(nx+x\right)\\ & = & \exp\left(nx\right)\exp\left(x\right)\\ & = & \left[\exp\left(x\right)\right]^{n}\exp\left(x\right)\\ & = & \left[\exp\left(x\right)\right]^{n+1} \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-7cbf43342d2e51f36d170376e91e220b_l3.png)
Pour finir, on sait que pour tout ![]() :
:
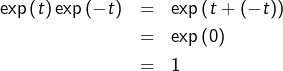
![Rendered by QuickLaTeX.com \begin{eqnarray*}\exp\left(nx\right) & = & \frac{1}{\exp\left(-nx\right)}\\ & = & \frac{1}{\left[\exp\left(x\right)\right]^{-n}}\\ & = & \left[\exp\left(x\right)\right]^{n} \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-34452061fe467e89b077f85094980fbd_l3.png)
Définition 3
On note désormais ![]() le réel
le réel ![]()
En choisissant ![]() dans la proposition précédente, on constate que :
dans la proposition précédente, on constate que :
![]()
Mais avant cela, nous allons définir ![]() pour
pour ![]() et
et ![]() quelconques.
quelconques.
5 – Puissances avec exposants rationnels
Le but de cette section est de définir proprement ce qu’on entend par ![]() lorsque
lorsque ![]() et
et ![]() sont deux entiers (
sont deux entiers (![]()
On y parviendra en trois étapes.
Etape 1
Dans un premier temps, étant donné ![]() on observe que l’application
on observe que l’application
![]()
- continue comme produit d’applications continues,
- injective parce que strictement croissante (sa dérivée est positive),
- surjective d’après le théorème des valeurs intermédiaires, après avoir vu que
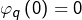 et que
et que 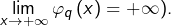
Sa bijection réciproque est donc aussi continue. Elle est appelée racine ![]() ème et notée :
ème et notée :
![]()
Le graphe de ![]() s’obtient par réflexion de celui de
s’obtient par réflexion de celui de ![]() par rapport à la droite d’équation
par rapport à la droite d’équation ![]()
En particulier, pour ![]() il s’agit de la célèbre racine carrée.
il s’agit de la célèbre racine carrée.
La figure ci-dessous correspond au cas ![]() (en bleu : le graphe de la fonction racine quatrième) :
(en bleu : le graphe de la fonction racine quatrième) :
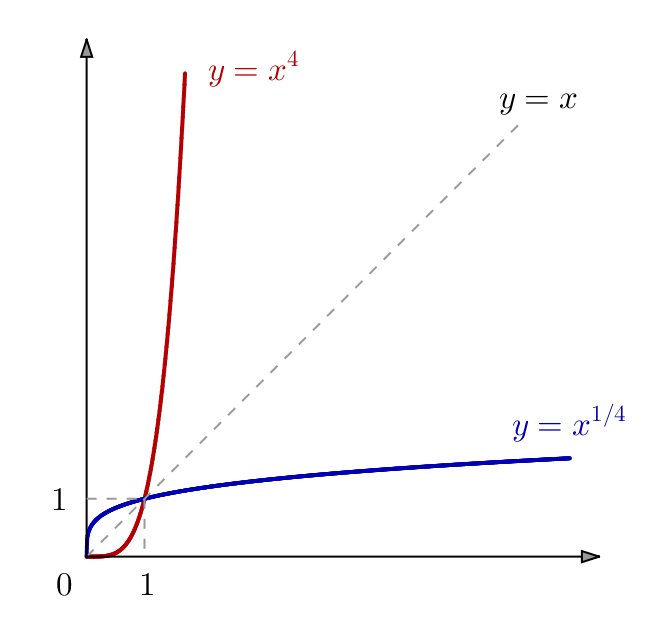
Démontrons un petit résultat préliminaire, qui nous servira à l’étape n° 2 :
Lemme 1
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
Preuve (cliquer pour déplier / replier)
D’une part (par définition d’une racine ![]() ème) :
ème) :
![]()
![]()
Etape 2
Etant donné un rationnel ![]() on va maintenant définir l’expression
on va maintenant définir l’expression ![]() toujours pour
toujours pour ![]()
Cette définition devra bien entendu être cohérente avec les deux cas particuliers déjà connus :
- celui où
 est un entier,
est un entier, - celui où
 est l’inverse d’un entier strictement positif.
est l’inverse d’un entier strictement positif.
Soient ![]() et
et ![]() tels que
tels que ![]() Il est naturel de poser :
Il est naturel de poser :
![]()
Il faut donc vérifier que l’expression ![]() ne dépend pas du couple (numérateur, dénominateur) choisi. C’est l’objet du point suivant.
ne dépend pas du couple (numérateur, dénominateur) choisi. C’est l’objet du point suivant.
Proposition 5
Si ![]() et
et ![]() sont tels que
sont tels que ![]() alors :
alors :
![]()
Preuve (cliquer pour déplier / replier)
D’une part :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left[\left(A^{c}\right)^{1/d}\right]^{b} & = & \left[\left(A^{1/d}\right)^{c}\right]^{b}\\ & = & \left(A^{1/d}\right)^{bc}\\ & = & \left(A^{1/d}\right)^{ad}\\ & = & \left[\left(A^{1/d}\right)^{d}\right]^{a}\\ & = & A^{a} \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-6cf465f21626ba6c754e46d318b4a015_l3.png)
Remarque
En fait, on peut se passer du lemme. Il suffit de calculer séparément ![]() et
et ![]() et de constater qu’il y a égalité (vu que
et de constater qu’il y a égalité (vu que ![]() par hypothèse).
par hypothèse).
Etape 3
Maintenant que l’expression ![]() est bien définie pour
est bien définie pour ![]() il est important de s’assurer que les formules connues pour les exposants entiers sont toujours valables.
il est important de s’assurer que les formules connues pour les exposants entiers sont toujours valables.
Proposition 6
Soient ![]() et
et ![]() Alors :
Alors :
Preuve (cliquer pour déplier / replier)
Posons ![]() et
et ![]() avec
avec ![]() et
et ![]()
- D’une part
![Rendered by QuickLaTeX.com \left(AB\right)^{r}=\left[\left(AB\right)^{a}\right]^{1/b}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d26a2d452cf4bf96f6343e8f55cd941d_l3.png) d’où :
d’où :
et d’autre part :![Rendered by QuickLaTeX.com \[\left[\left(AB\right)^{r}\right]^{b}=\left(AB\right)^{a}=A^{a}B^{a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-32586d57e10cb41f4c50b24d4211aa3b_l3.png)
Par injectivité de![Rendered by QuickLaTeX.com \[\left(A^{r}B^{r}\right)^{b}=\left(A^{r}\right)^{b}\left(B^{r}\right)^{b}=A^{a}B^{a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-77361a5903b923cfac36025199d5ac5d_l3.png)
![Rendered by QuickLaTeX.com \left]0,+\infty\right[\rightarrow\mathbb{R},\thinspace t\mapsto t^{b}](https://math-os.com/wp-content/ql-cache/quicklatex.com-b4510d16a8196ea6cc46282c3539e3eb_l3.png) il en résulte que :
il en résulte que :![Rendered by QuickLaTeX.com \[\boxed{\left(AB\right)^{r}=A^{r}B^{r}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f9fa9850430403e6fc0e2934fdcb76a3_l3.png)
- On observe que :
et de même![Rendered by QuickLaTeX.com \[\left(A^{r}\right)^{bd}=\left[\left(A^{r}\right)^{b}\right]^{d}=\left(A^{a}\right)^{d}=A^{ad}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0bc49852ee86df46fb1ff4aa7d19ac23_l3.png)
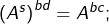 donc :
donc :
Et comme![Rendered by QuickLaTeX.com \[\left(A^{r}A^{s}\right)^{bd}=\left(A^{r}\right)^{bd}\left(A^{s}\right)^{bd}=A^{ad}A^{bc}=A^{ad+bc}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5cd7411fe9717859ee82bd002b2bc20f_l3.png)
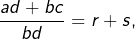 on en déduit que :
on en déduit que :![Rendered by QuickLaTeX.com \[\boxed{A^{r}A^{s}=A^{r+s}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec75dfb69d49cf57f5ce8626935cd58e_l3.png)
- Enfin
![Rendered by QuickLaTeX.com \left[\left(A^{r}\right)^{s}\right]^{d}=\left(A^{r}\right)^{c}](https://math-os.com/wp-content/ql-cache/quicklatex.com-032fa4ae3066d7e26edc9015bbfa975f_l3.png) et donc :
et donc :
et, par injectivité de![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\left(A^{r}\right)^{s}\right]^{bd} & = & \left(\left[\left(A^{r}\right)^{s}\right]^{d}\right)^{b}\\ & = & \left[\left(A^{r}\right)^{c}\right]^{b}\\ & = & \left(A^{r}\right)^{bc}\\ & = & \left[\left(A^{r}\right)^{b}\right]^{c}\\ & = & \left(A^{a}\right)^{c}\\ & = & A^{ac}\\ & = & \left(A^{rs}\right)^{bd} \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-0f2f82a36f2c1caa620d3486820e85c9_l3.png)
![Rendered by QuickLaTeX.com \left]0,+\infty\right[\rightarrow\mathbb{R},\thinspace t\mapsto t^{bd},](https://math-os.com/wp-content/ql-cache/quicklatex.com-9f28aaa9ffa30830b6df2dc2b973ca67_l3.png) on conclut que :
on conclut que :![Rendered by QuickLaTeX.com \[\boxed{\left(A^{r}\right)^{s}=A^{rs}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c0264937b0d731c7cb06ee4775dd59a9_l3.png)
Si ![]() et
et ![]() rationnel (non entier), peut-on encore parler de
rationnel (non entier), peut-on encore parler de ![]() ?
?
Oui et non …
On a vu que l’application ![]() (pour
(pour ![]() est bijective.
est bijective.
Mais si ![]() est un entier impair, on peut considérer l’application
est un entier impair, on peut considérer l’application
![]()
Par exemple, pour ![]() on définit ainsi la fonction racine cubique, qui est une bijection de
on définit ainsi la fonction racine cubique, qui est une bijection de ![]() dans
dans ![]() et l’on peut tout à fait écrire des égalités du genre :
et l’on peut tout à fait écrire des égalités du genre :
![]()
![]()
Mais ce point de vue soulève des difficultés. On constate par exemple que :
![]()
![]()
6 – Notation  : suite et fin
: suite et fin
On a vu à la fin de section 4 que :
![]()
Proposition 7
Pour tout ![]() :
:
![]()
Preuve (cliquer pour déplier / replier)
Soit ![]() et soient
et soient ![]() et
et ![]() tels que
tels que ![]() .
.
On observe (cf. proposition au début de la section 4) que :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left[\exp\left(r\right)\right]^{q} & = & \exp\left(qr\right)\\ & = & \exp\left(p\right)\\ & = & e^{p} \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6f31c499ac70ed78e5b2db85880fdfa_l3.png)
![]()
Il reste à donner un sens à ![]() pour
pour ![]() irrationnel … ce qu’on fait en posant la :
irrationnel … ce qu’on fait en posant la :
Définition 4
Si ![]() alors
alors ![]() désignera
désignera ![]()

Attention : il y a là une subtilité ! L’égalité ![]() a été prouvée pour
a été prouvée pour ![]() En revanche, pour
En revanche, pour ![]() elle est vraie par définition.
elle est vraie par définition.
Et la notation ![]() , dans tout ça ?
, dans tout ça ?
Dans l’introduction, on annonçait que cet article visait notamment à définir ![]() pour
pour ![]() et
et ![]() quelconque.
quelconque.
Si ![]() est rationnel, alors en notant
est rationnel, alors en notant ![]() avec
avec ![]() et
et ![]() :
:
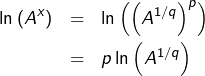
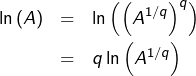
![]()
![]()
Illustration dynamique
Graphes des fonctions ![]() et
et ![]() .
.
Le bouton « Puissance / Exponentielle » permet de basculer de l’une à l’autre. Le slider contrôle la valeur du paramètre ![]() . On translate le système de coordonnées en cliquant / déplaçant. Les touches P et M (pour « + » et « -« ) permettent de zoomer / dézoomer.
. On translate le système de coordonnées en cliquant / déplaçant. Les touches P et M (pour « + » et « -« ) permettent de zoomer / dézoomer.
Convention
C’est par l’expression ![]() que l’on définit
que l’on définit ![]() lorsque
lorsque ![]() est irrationnel.
est irrationnel.
Pour ![]() cette définition n’apporte évidemment rien … mais on peut maintenant parler de
cette définition n’apporte évidemment rien … mais on peut maintenant parler de ![]() ou de
ou de ![]() ou encore de
ou encore de ![]() , etc …
, etc …
Cette convention doit être utilisée chaque fois qu’on étudie les variations d’une fonction du type ![]() En voici un exemple détaillé …
En voici un exemple détaillé …
7 – Une étude de variations
Nous allons nous intéresser aux variations de la fonction ![]() définie par :
définie par :
![Rendered by QuickLaTeX.com \[\boxed{f\left(x\right)=\left(1+\frac{1}{x}\right)^{x}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b1657314d5cf191cdd26c53aebfe12f3_l3.png)
L’expression ![]() désigne par définition
désigne par définition ![]() Elle est donc définie lorsque :
Elle est donc définie lorsque :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}f'\left(x\right) & = & f\left(x\right)\left[\ln\left(1+\frac{1}{x}\right)+x\,\frac{-\frac{1}{x^{2}}}{1+\frac{1}{x}}\right]\\ & = & f\left(x\right)\left[\ln\left(1+\frac{1}{x}\right)-\frac{1}{x+1}\right] \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-137fcfdf2528533e14b9ab60ddffb120_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{g\left(x\right)=\ln\left(1+\frac{1}{x}\right)-\frac{1}{x+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-866b8e4ab9a8d42bfdf906ae88e1eb84_l3.png)
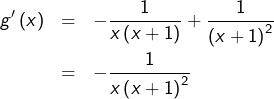
Ainsi, ![]() croît strictement sur chacun des intervalles
croît strictement sur chacun des intervalles ![]() et
et ![]()
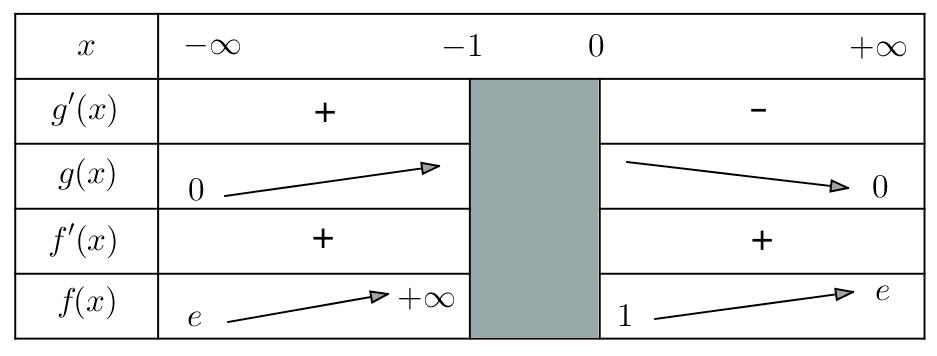
On calcule ensuite :
![Rendered by QuickLaTeX.com \[\ln\left(f\left(x\right)\right)=\frac{\ln\left(1+\frac{1}{x}\right)}{\frac{1}{x}}\mbox{ donc }\lim_{x\rightarrow\pm\infty}\ln\left(f\left(x\right)\right)=1\mbox{ puis }\boxed{\lim_{x\rightarrow\pm\infty}f\left(x\right)=e}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d359d84bb3f902474963e5022c233733_l3.png)
![]()
![]()
Ces divers éléments permettent de connaître l’allure du graphe de ![]() :
:
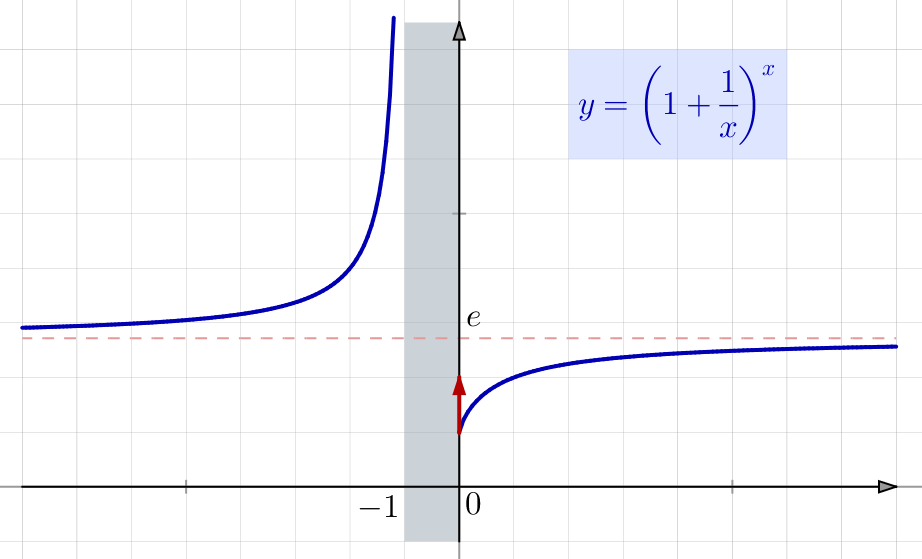
Une retombée de ce qui précède est la convergence de la suite de terme général :
![]()
Intérêts composés (cliquer pour déplier / replier)
Admettons qu’une somme ![]() soit placée avec un taux d’intérêt annuel
soit placée avec un taux d’intérêt annuel ![]()
Supposons que le versement des intérêts se fasse à la fin de chaque mois et notons ![]() le montant épargné (capital + intérêts) à l’issue du
le montant épargné (capital + intérêts) à l’issue du ![]() ème mois.
ème mois.
Alors, ![]() et pour tout
et pour tout ![]() :
:
![]()
![]()
![]()
![]()
8 – La série exponentielle
A la fin de la section précédente, est apparue la suite de terme général :
![]()
Cette convergence est lente : on peut montrer que l’écart
![]()
![Rendered by QuickLaTeX.com \[x_{n}=\sum_{k=0}^{n}\frac{1}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6332c02ede61e8bca58ed9914dbb7288_l3.png)
Théorème (formule de Taylor avec reste intégral)
Si ![]() est un intervalle (non trivial) et si
est un intervalle (non trivial) et si ![]() est indéfiniment dérivable, alors pour tout couple
est indéfiniment dérivable, alors pour tout couple ![]() d’éléments de
d’éléments de ![]() :
:
![Rendered by QuickLaTeX.com \[ f\left(x\right)=\sum_{k=0}^{n}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}\frac{\left(x-t\right)^{n}}{n!}f^{\left(n+1\right)}\left(t\right)\thinspace dt \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dd96fb20ded5105ebec9fe73caaf9ab2_l3.png)
Cette formule est d’apparence compliquée. Pourtant, elle est assez simple à prouver, en combinant un raisonnement par récurrence et une intégration par parties.
Preuve (cliquer pour déplier / replier)
Initialisation – On sait bien que :
![]()
Hérédité – En supposant l’égalité établie pour un certain rang
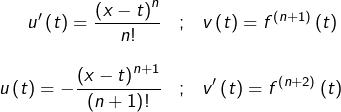
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{a}^{x}\frac{\left(x-t\right)^{n}}{n!}f^{\left(n+1\right)}\left(t\right)\thinspace dt & = & \left[-\frac{\left(x-t\right)^{n+1}}{\left(n+1\right)!}f^{\left(n+1\right)}\left(t\right)\right]_{t=a}^{x}\\& & +\int_{a}^{x}\frac{\left(x-t\right)^{n+1}}{\left(n+1\right)!}f^{\left(n+2\right)}\left(t\right)\thinspace dt\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d21375c6a406fb1c43bdda281be4e33_l3.png)
![Rendered by QuickLaTeX.com \[f\left(x\right)=\sum_{k=0}^{n+1}\frac{f^{\left(k\right)}\left(a\right)}{k!}\left(x-a\right)^{k}+\int_{a}^{x}\frac{\left(x-t\right)^{n+1}}{\left(n+1\right)!}f^{\left(n+2\right)}\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2ce59da5c8bcec2fb85426a6abede120_l3.png)
Appliquons ce résultat au cas particulier suivant :
![]()
On obtient, pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[e^{x}=\sum_{k=0}^{n}\frac{x^{k}}{k!}+\int_{0}^{x}\frac{\left(x-t\right)^{n}}{n!}e^{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fae5b980550b179c939cf9bc0ba40e54_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\mathbb{R},\thinspace e^{x}=\sum_{k=0}^{\infty}\frac{x^{k}}{k!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-efa2cae5d7635b87f6860ab519b7e7e3_l3.png)
Prouvons la relation ![]() en commençant par un petit lemme.
en commençant par un petit lemme.
Lemme 2
Pour tout ![]() :
:
![]()
Preuve (cliquer pour déplier / replier)
Il suffit de traiter le cas ![]() Si l’on pose, pour tout
Si l’on pose, pour tout ![]() :
:
![]()
![]()
![]()
La suite ![]() est donc décroissante à partir d’un certain rang. Comme elle est minorée par 0, elle converge. Notons
est donc décroissante à partir d’un certain rang. Comme elle est minorée par 0, elle converge. Notons ![]() sa limite; en passant à la limite dans l’égalité :
sa limite; en passant à la limite dans l’égalité :
![]()
On peut maintenant prouver la relation ![]() Pour plus de clarté, séparons les cas
Pour plus de clarté, séparons les cas ![]() et
et ![]() Rappelons que nous avons posé, un peu plus haut :
Rappelons que nous avons posé, un peu plus haut :
![Rendered by QuickLaTeX.com \[\boxed{R_{n}\left(x\right)=\int_{0}^{x}\frac{\left(x-t\right)^{n}}{n!}\thinspace e^{t}\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b237b5997ce4a1f9651c2a10563c071a_l3.png)
Premier cas : 
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
![]()
Deuxième cas : 
On commence par observer que :
![]()
![]()
Tout ceci montre que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[e^{x}=\sum_{k=0}^{\infty}\frac{x^{k}}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9b873e305cac8eca39138f2c708fa171_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{e=\sum_{k=0}^{\infty}\frac{1}{k!}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ba6026880769432641574aa3c23a66a_l3.png)
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=0}^{n}\frac{1}{k!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d98baf98661fdbc6ce507245e8512e9_l3.png)
9 – Irrationalité du nombre e
En théorie des nombres, une question importante (et généralement difficile d’accès) consiste à décider si un réel ![]() donné est rationnel ou non.
donné est rationnel ou non.
Pour des raisons non développées dans cet article, il est précieux de disposer de suites convergeant rapidement (en un sens à préciser) vers ![]()
Or, c’est justement le cas des suites de termes généraux :
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=0}^{n}\frac{1}{k!}\qquad\text{et}\qquad T_{n}=S_{n}+\frac{1}{n\:n!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d360e1b4d14a68fdb3093e165483d92c_l3.png)
Comme pour tout ![]() :
:
![]()
Maintenant, démontrons par l’absurde la :
Proposition 8
Le nombre e est irrationnel.
Preuve (cliquer pour déplier / replier)
En supposant ![]() rationnel, donc de la forme :
rationnel, donc de la forme :
![]()
![]()
![]()
Or ![]() est entier et de plus :
est entier et de plus :
![]()
![]()
L’irrationalité du nombre ![]() est ainsi établie. Vous pourrez retrouver cette preuve dans une vidéo consacrée à l’irrationalité des nombres
est ainsi établie. Vous pourrez retrouver cette preuve dans une vidéo consacrée à l’irrationalité des nombres ![]() et
et ![]()
Un résultat meilleur, mais plus difficile d’accès, établit la transcendance du nombre ![]()
Il est dû au mathématicien français Charles Hermite (1822 – 1901), qui le publia en 1873.
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonsoir Monsieur,
Dans la preuve finale de l’article de l’irrationalité de e, bien que l’on comprenne très bien la preuve, il me semble que les suites x et y ont remplacé sans transition les suites S et T 🙂
Bien à vous.
Ah ! oui … Merci de me l’avoir signalé. C’est réglé, j’ai mis des S et des T de partout 🙂