Lettre J
JENSEN (inégalité de)
Soit ![]() un intervalle non trivial et soit
un intervalle non trivial et soit ![]() une application convexe. Alors :
une application convexe. Alors :
Théorème
Soit un entier ![]() ainsi que
ainsi que ![]() et
et ![]() tel que
tel que 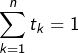 . Alors :
. Alors :
![Rendered by QuickLaTeX.com \[f\left(\sum_{k=1}^{n}t_{k}x_{k}\right)\leqslant\sum_{k=1}^{n}t_{k}\thinspace f\left(t_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f53b443f576a50cdde9ea264a3741738_l3.png)
Cette inégalité est attribuée au mathématicien danois Johan Jensen (1859 – 1925).

La preuve se fait par récurrence. Pour ![]() c’est la définition de la convexité. En supposant le résultat établi au rang
c’est la définition de la convexité. En supposant le résultat établi au rang ![]() pour un certain
pour un certain ![]() on se donne
on se donne ![]() et
et ![]() tels que
tels que 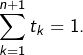 Si
Si ![]() alors
alors ![]() pour tout
pour tout ![]() et il n’y a rien à démontrer. Et si
et il n’y a rien à démontrer. Et si ![]() alors en posant
alors en posant 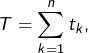 on voit que
on voit que ![]() et que :
et que :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n+1}t_{k}x_{k}=T\sum_{k=1}^{n}\dfrac{t_{k}}{T}\thinspace x_{k}+\left(1-T\right)x_{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53c739ff3e11956aa51554bd13b1c62c_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\sum_{k=1}^{n+1}t_{k}x_{k}\right)\leqslant T\thinspace f\left(\sum_{k=1}^{n}\dfrac{t_{k}}{T}\thinspace x_{k}\right)+\left(1-T\right)\thinspace f\left(x_{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-955f38eb7d2071fe076ba9412b72de1e_l3.png)
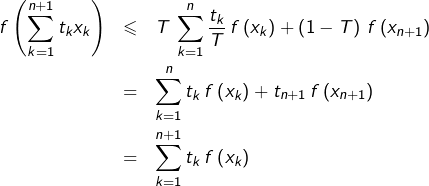
On appelle aussi inégalité de Jensen la version continue de ce qui précède :
Théorème
Soit ![]() une application continue. On suppose que
une application continue. On suppose que ![]() est un intervalle non trivial, que
est un intervalle non trivial, que ![]() et que
et que ![]() est convexe. Alors :
est convexe. Alors :
![]()
Exercice pour le lecteur : déduire cette inégalité de la version discrète énoncée plus haut, en utilisant le théorème de convergence des sommes de Riemann.
JORDAN (matrice de)
Etant donné un entier ![]() on appelle matrice (ou cellule) de Jordan de taille
on appelle matrice (ou cellule) de Jordan de taille ![]() la matrice
la matrice ![]() , considérée comme élément de l’algèbre
, considérée comme élément de l’algèbre ![]() .
.
Les termes de cette matrice sont donc tous nuls, à l’exception de ceux situés sur la « sur-diagonale », qui valent 1. Ci-dessous les matrices ![]() et
et ![]() :
:
![Rendered by QuickLaTeX.com \[J_{2}=\left[\begin{array}{cc}0 & 1\\0 & 0\end{array}\right]\qquad J_{5}=\left[\begin{array}{ccccc}0 & 1 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 1\\0 & 0 & 0 & 0 & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64081feb7a1888aa1f1dff3280733456_l3.png)
L’endomorphisme ![]() canoniquement associé à
canoniquement associé à ![]() est défini par :
est défini par :
![]()
Théorème (réduction de Jordan – cas nilpotent)
Si ![]() est un
est un ![]() espace vectoriel de dimension
espace vectoriel de dimension ![]() et si
et si ![]() est nilpotent, alors il existe une base de
est nilpotent, alors il existe une base de ![]() dans laquelle
dans laquelle ![]() est représenté par une matrice diagonale par blocs, chaque bloc étant une matrice de Jordan.
est représenté par une matrice diagonale par blocs, chaque bloc étant une matrice de Jordan.
Une conséquence est l’important théorème suivant :
Théorème (réduction de Jordan – cas général)
Soit ![]() est un
est un ![]() espace vectoriel de dimension
espace vectoriel de dimension ![]() et soit
et soit ![]() dont le polynôme caractéristique est scindé. Alors il existe une base de
dont le polynôme caractéristique est scindé. Alors il existe une base de ![]() dans laquelle
dans laquelle ![]() est représenté par une matrice diagonale par blocs, chaque bloc étant de la forme
est représenté par une matrice diagonale par blocs, chaque bloc étant de la forme ![]() où
où ![]() est une valeur propre de
est une valeur propre de ![]()
Le second théorème se démontre à partir du premier de la manière suivante. On note ![]() le polynôme caractéristique de
le polynôme caractéristique de ![]() Comme
Comme ![]() est scindé dans
est scindé dans ![]() il en va de même du polynôme minimal de
il en va de même du polynôme minimal de ![]() noté
noté ![]() On peut donc écrire :
On peut donc écrire :
![Rendered by QuickLaTeX.com \[\mu_{f}=\prod_{i=1}^{p}\left(X-\lambda_{i}\right)^{r_{i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07f3f8f6284fe6ee46453385db65b1bd_l3.png)
Le lemme de décomposition des noyaux donne
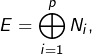 où les
où les ![]()
- la restriction de
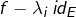 à
à 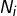 est nilpotente d’indice
est nilpotente d’indice 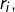
- la dimension de
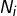 est égale à la multiplicité
est égale à la multiplicité 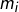 de
de 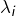 en tant que racine de
en tant que racine de 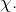
Il existe donc, d’après le premier théorème, une base de ![]() dans laquelle la restriction de
dans laquelle la restriction de ![]() est représentée par une matrice diagonale par blocs, chaque bloc étant de la forme
est représentée par une matrice diagonale par blocs, chaque bloc étant de la forme ![]() Il ne reste plus qu’à concaténer ces bases, ce qui fournit une base de
Il ne reste plus qu’à concaténer ces bases, ce qui fournit une base de ![]() dans laquelle la matrice de
dans laquelle la matrice de ![]() possède la forme voulue.
possède la forme voulue.

