Neuf énoncés d’exercices sur la factorielle (fiche 01).
Calculer plus simplement la somme :
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=1}^{n}k\thinspace k!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7712064914cc8344f5d10a92828f2e16_l3.png)
⇨ Pour vous « refaire une santé » sur les manipulations de somme, consultez cet article.
⇨ Pour réviser le concept de factorielle d’un entier naturel, les points d’entrée sont cet article de vulgarisation et cet article de niveau supérieur.
Dans la fraction suivante, le numérateur est le produit des ![]() premiers nombres impairs, et le dénominateur est le produit des
premiers nombres impairs, et le dénominateur est le produit des ![]() premiers nombres pairs :
premiers nombres pairs :
![]()
Exprimer ![]() d’une manière plus « compacte », au moyen de factorielles.
d’une manière plus « compacte », au moyen de factorielles.


Quels sont les entiers naturels ![]() pour lesquels le nombre de chiffres décimaux de
pour lesquels le nombre de chiffres décimaux de ![]() est précisément égal à
est précisément égal à ![]() ? Prouver qu’il n’existe aucun entier
? Prouver qu’il n’existe aucun entier ![]() vérifiant cette condition.
vérifiant cette condition.

Soient ![]() des réels strictement positifs. Montrer que la suite de terme général :
des réels strictement positifs. Montrer que la suite de terme général :
![]()

Etablir, pour tout ![]() l’inégalité :
l’inégalité :
![]()

Pour tout ![]() on pose :
on pose :
![]()
Après avoir établi la convergence de cette intégrale, calculer

Résoudre dans ![]() l’équation :
l’équation :
![]()

L’égalité suivante est vraie :
![Rendered by QuickLaTeX.com \[ \frac{28}{17}=\frac{\left(2!\right)^{4}\times\left(7!\right)^{2}\times13!}{\left(3!\right)^{2}\times5!\times17!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0d1e48ab0cd6034b691cb83a85e0d4db_l3.png)
Montrer, plus généralement, que tout rationnel strictement positif peut s’écrire comme un produit de factorielles de nombres premiers ou comme le quotient de deux tels produits.

Montrer que tout entier ![]() peut s’écrire de façon unique sous la forme :
peut s’écrire de façon unique sous la forme :
![Rendered by QuickLaTeX.com \[A=\sum_{k=1}^{n}\,a_{k}\,k!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa0def2391116c7fa4ae5cc417560c7b_l3.png)
avec les conditions :
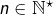
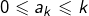 pour tout
pour tout 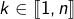
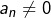
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions


Desole’ pour le precedent commentaire. En fait si r_n (n-i)!, on continue ainsi jusqu’a` ce que la derniere division euclienne ait un reste nul comme indique’ dans la solution.
A propos de l’exercice #9:
On effectue les division euclidiennes suivantes:
A = n! * a_n + r_n
r_n = (n-1)! * a_n-1 + r_n-1
et ainsi de suite.
Mais comment prouve t’on que r_n est superieur a` (n-1)! ?
que r_n-1 > (n-2)! etc.
Pour diviser un entier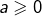 par un entier
par un entier 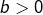 , on n’a pas besoin de supposer
, on n’a pas besoin de supposer 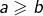 .
. ).
).
Si tel n’est pas le cas, le quotient sera simplement nul (et le reste égal à
A propos de l’exercice #8:
« tout k dans {2,…, q-1} est un produit de nombres premiers p. Par consequent q-1 = 2*q’ . Comment prouve t’on alors que q’ <= p et par consequent tous les sous-multiples de q' aussi <= p.
Est ce demontre' dans la litterature? Que se passe t'il pour les premiers tres grands? Est ce toujours le cas?
– joseph
Dans la solution proposée, on définit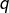 comme le plus petit nombre premier
comme le plus petit nombre premier 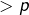 . Evidemment,
. Evidemment,  est pair donc de la forme
est pair donc de la forme 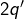 . Attention,
. Attention, 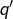 n’a aucune raison d’être premier, mais cet entier est produit de nombres premiers
n’a aucune raison d’être premier, mais cet entier est produit de nombres premiers 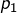 , …
, … 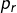 avec
avec 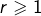 . Chacun des
. Chacun des 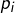 est
est 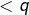 et donc
et donc 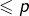 en raison de la définition de
en raison de la définition de 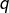 . Je ne vois pas de difficulté ici. Et l’on peut donc, si l’on veut, appliquer l’hypothèse de récurrence à chacun des
. Je ne vois pas de difficulté ici. Et l’on peut donc, si l’on veut, appliquer l’hypothèse de récurrence à chacun des 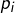 mais cela donnera une décomposition (en produit de factorielles de nombres premiers ou en quotient de tels produits) pour
mais cela donnera une décomposition (en produit de factorielles de nombres premiers ou en quotient de tels produits) pour  et non pas pour
et non pas pour 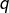 … à moins que vous ne cherchiez pas à suivre la solution proposée ? Dans ce cas, merci de préciser.
… à moins que vous ne cherchiez pas à suivre la solution proposée ? Dans ce cas, merci de préciser.
« Chacun des pi est < q et donc p (de meme (q-1) > p ) et qi < q -1 ou` les qi sont les facteurs premiers de la decomposition de (q-1)/2. Il me semble qu'on ne peut pas conclure a` moins de prouver que l'ecart entre deux nombres premiers consecutifs est toujours plus petit que (q-1)/2 soit que
(q-1)/2 < p et donc tous les qi < p
Peut-être n’avez vous pas noté que, dans la solution proposée,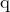 désigne le plus petit nombre premier supérieur à
désigne le plus petit nombre premier supérieur à 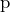 . Il en résulte inévitablement que les facteurs premiers de
. Il en résulte inévitablement que les facteurs premiers de 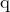 -1 sont inférieurs ou égaux à
-1 sont inférieurs ou égaux à 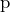 puisqu’ils sont strictement inférieurs à
puisqu’ils sont strictement inférieurs à 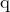 .
.
Je vous invite, par ailleurs, à placer en tête d’un commentaire le shortcode :
[ latexpage ]
(sans les espaces) ce qui vous permet ensuite de placer des commandes LaTeX dans le texte.
Autre remarque toujours a` propos de l’exercice #5, la solution qui utilise le developpement en series de l’exponentielle n’est elle pas en fait une inegalite’ strictement superieur?
Oui, comme je l’ai d’ailleurs indiqué en réponse au commentaire précédent, l’inégalité est stricte pour non nul. On peut aussi voir que, pour
non nul. On peut aussi voir que, pour 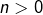 ,
, 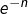 est irrationnel tandis
est irrationnel tandis 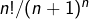 est rationnel : l’inégalité est donc nécessairement stricte.
est rationnel : l’inégalité est donc nécessairement stricte.
Bien entendu, il n’est pas incorrect d’écrire une égalité large en pareil cas !
Bonjour – A propos de l’exercice #5, en fin de la solution de l’exercice, la premiere inegalite’ ne serait elle pas en fait une egalite’ suivie d’une inegalite’. La conclusion est correcte mais la premiere inegalite’ a` gauche me semble etre une egalite’ base’e sur le developpement en series de l’exponentielle.
Non, il s’agit bien d’une inégalité (qui est d’ailleurs stricte dès que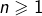 ).
). .
.
Il s’agirait d’une égalité si la sommation s’étendait jusqu’à l’infini, mais la somme écrite est seulement indexée de 0 à
Bonjour, j’ai rec,u une reponse partielle par email, mais le email semble coupe’. Je n’ai pu donc pas voir la suite a` ma question precedente.
– j.c.
Par ailleurs, on sait que pour tout n dans N*, le nombre de chiffres décimaux de n est
Cn = 1 + log(n!)
Qui devrait etre le nombre de chiffres décimaux de n! et non n… faute de frappe?
Non, pas de faute de frappe dans l’indication donnée pour l’exercice 3. La formule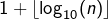 donne le nombre de chiffres décimaux de
donne le nombre de chiffres décimaux de  , pour tout entier
, pour tout entier 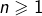 . Cela dit, comme ceci est vrai pour tout
. Cela dit, comme ceci est vrai pour tout  , on peut l’appliquer à qui on veut… par exemple à la factorielle de
, on peut l’appliquer à qui on veut… par exemple à la factorielle de  .
.
Bonjour – toujours a` propos de l’exercice #3.
L’ennonce’ precise de demontrer que tout « n » > 100 ne verifie pas la condition. Lors de la demo, on montre que U(n) est strictement croissante des que n >= 9 puis que pour n >=25, alors C(n) > n et ainsi le nombre de decimaux de n! est des lors toujours plus grand que « n ».
Je ne vois pas la relation entre le rang = 9, n>=25 et la question de depart « n » >= 100.
Un peu confus je dois dire.
Merci d’avance.
– jc
La suite u est strictement croissante à partir du rang 9. Par conséquent, si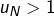 pour un certain
pour un certain 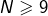 , alors on peut être certain que
, alors on peut être certain que 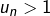 pour tout entier
pour tout entier  .
.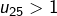 , alors
, alors 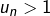 pour tout
pour tout  .
. ne convient (et a fortiori qu’aucun entier
ne convient (et a fortiori qu’aucun entier 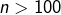 ne convient !).
ne convient !).
Comme
Ceci montre qu’aucun entier
j’espère que c’est plus clair à présent.