1 – Cinq livres à lire … mais dans quel ordre ?
Vous êtes sur le point de partir en vacances…
Comme vous aimez lire des romans, vous vous apprêtez à en choisir cinq pour les dévorer le soir, confortablement installé(e) dans un endroit calme. Une fois les bouquins choisis, une question subsiste : dans quel ordre allez-vous les lire ?
Pour simplifier les choses, repérons chacun de ces cinq livres par sa couleur :
Vous pourrez éventuellement commencer par le rouge, puis continuer avec le jaune, le violet, le vert et enfin le bleu.
Mais vous pourriez tout aussi bien démarrer avec le jaune, enchaîner avec le bleu, puis le rouge, le vert et terminer avec le violet.
Il existe, semble-t-il, de nombreuses possibilités … mais combien au juste ?
La réponse est « factorielle 5 », c’est-à-dire 5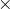 4
4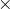 3
3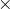 2
2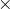 1 soit 120 possibilités.
1 soit 120 possibilités.
C’est assez facile à comprendre : le premier livre que vous lirez peut être choisi de 5 manières. Pour chaque tel choix, le second livre peut être choisi de 4 manières et il existe donc 5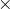 4 = 20 façons de choisir les deux premiers livres. Le troisième livre peut alors être choisi de 3 façons et nous en sommes à 5
4 = 20 façons de choisir les deux premiers livres. Le troisième livre peut alors être choisi de 3 façons et nous en sommes à 5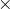 4
4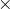 3 = 60 scénarios envisageables pour les trois premiers livres. Arrive alors le quatrième livre, qui peut être choisi de 2 façons. Quant au cinquième et dernier, il ne peut pas être choisi : il est imposé !
3 = 60 scénarios envisageables pour les trois premiers livres. Arrive alors le quatrième livre, qui peut être choisi de 2 façons. Quant au cinquième et dernier, il ne peut pas être choisi : il est imposé !
2 – La factorielle d’un entier
Plus généralement, si  est un entier supérieur ou égal à 1, on désigne par « factorielle
est un entier supérieur ou égal à 1, on désigne par « factorielle  » le produit des entiers de 1 à
» le produit des entiers de 1 à 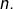 Cet entier est noté
Cet entier est noté 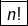 et le tableau ci-dessous indique les valeurs des premiers termes de cette suite :
et le tableau ci-dessous indique les valeurs des premiers termes de cette suite :
Le produit des entiers de 1 à  est clairement égal au produit de
est clairement égal au produit de  par le produit des entiers de 1 à
par le produit des entiers de 1 à 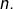 Autrement dit, pour tout
Autrement dit, pour tout 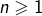 :
:
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\left(n+1\right)!=\left(n+1\right)\:n!$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2379ec1552ba783065687c327af070da_l3.png)
On peut définir la factorielle de 0 en faisant en sorte que cette formule de récurrence soit respectée pour 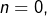 ce qui conduit à poser :
ce qui conduit à poser :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$0!=1$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-04004d2a881a319f4c60c504c7680eae_l3.png)
En généralisant ce qui a été dit plus haut au sujet des 5 livres, on voit que l’entier 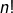 s’interprète comme le nombre de façons de permuter
s’interprète comme le nombre de façons de permuter  objets.
objets.
3 – Permutations d’un jeu de cartes
Etant donné un jeu de 52 cartes, le nombre de façons de les ordonner est donc 52!.
Il s’agit d’un entier absolument colossal. Le voici, en chair et en os :
52! = 80658175170943878571660636856403766975289505440883277824000000000000
soit environ 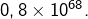
Ce nombre est tellement grand qu’il n’est pas du tout évident de s’en faire une idée un tant soit peu concrète, mais j’ai découvert sur ce site une interprétation géniale et je ne résiste pas au plaisir de la partager avec vous … Je pense que les bonnes idées doivent être diffusées largement !
Voici donc une histoire qui se déroule en 52! secondes …
Asseyez-vous confortablement : ça va durer un moment 😊
Un type marche le long de l’équateur terrestre (environ 40 000 km) à raison d’un pas tous les milliards d’années.
S’il franchit un mètre à chaque pas, il ne lui faudra donc pas moins de 40 000 000 000 000 000 années (quarante millions de milliards !) pour faire le tour de la terre (une durée TRES largement supérieure à l’âge de l’univers… mais bon).
Lorsqu’il a terminé de faire le tour du globe, il prend la pipette qu’il a dans sa poche et prélève une goutte d’eau dans l’océan pacifique, puis repart pour le tour suivant, toujours au même rythme d’un pas tous les milliards d’années. A la fin du second tour, il prélève une seconde goutte avec sa pipette et ainsi de suite …
Je me suis laissé dire que l’océan pacifique renfermerait environ 700 000 000 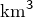 d’eau. Par ailleurs, on peut raisonnablement accepter qu’un centimètre cube d’eau permet de former 20 gouttes … Il va donc falloir « un certain temps » (comme l’aurait dit Fernand Reynaud) à notre personnage pour vider l’océan ! Mais il va finir par y arriver.
d’eau. Par ailleurs, on peut raisonnablement accepter qu’un centimètre cube d’eau permet de former 20 gouttes … Il va donc falloir « un certain temps » (comme l’aurait dit Fernand Reynaud) à notre personnage pour vider l’océan ! Mais il va finir par y arriver.
Au passage, on peut se demander où il va entreposer toute l’eau qu’il en extrait … mais l’histoire ne le dit pas … et on n’est plus à ça près 🙂
Donc, lorsque l’océan est vide, notre ami y reverse toute l’eau (!) puis dépose une feuille de papier sur la table qui se trouve devant lui.
Et il redémarre : un tour du monde … une goutte … un tour du monde … une goutte … etc …
A chaque fois que l’océan se retrouve vide, il le remplit de nouveau, puis dépose une nouvelle feuille de papier sur la pile.
L’épaisseur de la pile de feuille augmente donc progressivement et, au bout d’une très très longue durée, elle finira par atteindre la valeur de la distance terre-soleil, soit environ 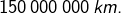
Et là, vous vous dites que c’est bon, on a terminé ! Eh bien non, car à ce moment là, notre personnage doit reprendre tout le processus 3000 fois !!
Et c’est seulement à l’issue de la 3000-ème étape qu’il se sera écoulé (en gros) 52! secondes.
Vous n’y croyez pas ? Il faut reconnaître que c’est difficile à croire, mais les faits sont têtus :
Le temps nécessaire pour un tour du globe est 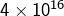 années, soit (en secondes) :
années, soit (en secondes) :
![Rendered by QuickLaTeX.com \[T=4\times10^{16}\times365\times24\times3600=1\thinspace261\thinspace440\thinspace000\thinspace\times10^{15}\thinspace s\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-592872fae308caf7cf842e81f7434012_l3.png)
Comme l’océan renferme :
![Rendered by QuickLaTeX.com \[N=700\thinspace000\thinspace000\times100\thinspace000^{3}\times20\thinspace\text{ gouttes d'eau}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-de7e9fcfd8b45e0bd352bda3203c30d1_l3.png)
il faudra patienter :
![Rendered by QuickLaTeX.com \[N\times T=1766016\times10^{43}\thinspace s\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-16eefdf0324c65a82ae903e3eda7f5cf_l3.png)
Ensuite, en admettant que les feuilles de papier aient une épaisseur d’un dixième de millimètre, il faudra en tout :
![Rendered by QuickLaTeX.com \[\frac{150\thinspace000\thinspace000\thinspace000\thinspace000}{0,1}\:\text{feuilles}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a9dc9206f66db54dd4b0841bbb7568e4_l3.png)
pour que la pile atteigne l’épaisseur voulue.
Au total, la durée nécessaire pour l’ensemble du processus est :
![Rendered by QuickLaTeX.com \[D=3000\times1766016\times10^{43}\times1\thinspace500\thinspace000\thinspace000\thinspace000\thinspace000\thinspace s\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f023e22514da6f473db24119c3ad3616_l3.png)
soit :
![Rendered by QuickLaTeX.com \[D\simeq0,8\times10^{68}\thinspace s\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-597f619ffb31137c351feae89a4ced7b_l3.png)
On retrouve bien un nombre du même ordre de grandeur que 52!
Sympa, non ?
Ma contribution, pour cette interprétation de la factorielle de 52, se résume à l’adaptation d’un article original en anglais (lien donné plus haut) et aux illustrations 🙂
Dans un prochain article sur la factorielle, nous commencerons à faire des maths un peu plus substantielles à ce sujet !
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
J’aime ça :
J’aime chargement…

![]() 4
4![]() 3
3![]() 2
2![]() 1 soit 120 possibilités.
1 soit 120 possibilités.![]() 4 = 20 façons de choisir les deux premiers livres. Le troisième livre peut alors être choisi de 3 façons et nous en sommes à 5
4 = 20 façons de choisir les deux premiers livres. Le troisième livre peut alors être choisi de 3 façons et nous en sommes à 5![]() 4
4![]() 3 = 60 scénarios envisageables pour les trois premiers livres. Arrive alors le quatrième livre, qui peut être choisi de 2 façons. Quant au cinquième et dernier, il ne peut pas être choisi : il est imposé !
3 = 60 scénarios envisageables pour les trois premiers livres. Arrive alors le quatrième livre, qui peut être choisi de 2 façons. Quant au cinquième et dernier, il ne peut pas être choisi : il est imposé !
![]()
![]()
![]() d’eau. Par ailleurs, on peut raisonnablement accepter qu’un centimètre cube d’eau permet de former 20 gouttes … Il va donc falloir « un certain temps » (comme l’aurait dit Fernand Reynaud) à notre personnage pour vider l’océan ! Mais il va finir par y arriver.
d’eau. Par ailleurs, on peut raisonnablement accepter qu’un centimètre cube d’eau permet de former 20 gouttes … Il va donc falloir « un certain temps » (comme l’aurait dit Fernand Reynaud) à notre personnage pour vider l’océan ! Mais il va finir par y arriver.![]()
![]()
![]()
![]()
![]()
![]()





Une bien jolie façon de se représenter cette factorielle… Merci beaucoup, promenade très intéressante!!
Magnifique…VERTIGINEUX la fable sur 52!