Neuf énoncés d’exercices sur le second degré (fiche 02).
Avant tout, rappelons ce qu’il faut savoir concernant le signe d’un trinôme du second degré.
Posons pour tout ![]() :
:
![]()
![]()
Lorsque ![]() on note
on note ![]() les racines de
les racines de ![]()
Illustration dynamique
Le graphe du trinôme ![]() est tracé :
est tracé :
- en rouge si
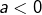 ,
, - en vert si
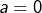 ,
, - en bleu si
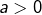
Lorsque ![]() , les deux racines
, les deux racines ![]() sont matérialisées par deux petits disques centrés respectivement en
sont matérialisées par deux petits disques centrés respectivement en ![]() et en
et en ![]() .
.
La valeur du discriminant est affichée en rouge ou en bleu (et exceptionnellement en vert …), selon son signe.
Les sliders permettent d’apprécier comment se déforme la courbe lorsque ![]() varient.
varient.
On note ![]() pour indiquer que
pour indiquer que ![]() et
et ![]() sont de même signe.
sont de même signe.
- si
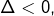 alors
alors 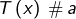 pour tout
pour tout 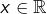
- si
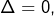 alors
alors 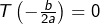 et
et 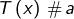 pour tout
pour tout 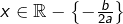
- si
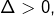 alors :
alors :
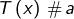 pour tout
pour tout ![Rendered by QuickLaTeX.com x\in\left]-\infty,\alpha\right[\cup\left]\beta,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-bde45b3de691ffb9c9cf0f15a27ff691_l3.png)
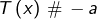 pour tout
pour tout ![Rendered by QuickLaTeX.com x\in\left]\alpha,\beta\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c1629f4f3b70b3d96faf53284491392_l3.png)
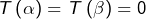
Rappelons aussi les relations entre coefficients et racines :
![]()

Résoudre chacune des inéquations :
![Rendered by QuickLaTeX.com \[\begin{matrix}x^{2}<10x & ; & x^{2}\geqslant2x-1 & ; & x^{2}-6x+8>0\\\\x^{2}-x+1>0 & ; & 7x^{2}-11x+4\leqslant0 & ; & 70x^{2}-53x+10<0\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ae4ef69a803aa9fd7462f645c1dbed50_l3.png)

Qu’y-a-t-il d’incorrect dans la résolution de l’inéquation suivante ?
![]()
![]()
![]()
![]()
![]()

Résoudre chacune des inéquations :
![]()

Décider, pour chacun des trois nombres :
![]()

Comment choisir le réel m de telle sorte que l’équation (d’inconnue ![]() ) :
) :
![]()

Comment choisir le réel ![]() de telle sorte que l’équation (d’inconnue
de telle sorte que l’équation (d’inconnue ![]() ) :
) :
![]()

On note ![]() les solutions de l’équation
les solutions de l’équation ![]() Sans chercher à déterminer séparément
Sans chercher à déterminer séparément ![]() et
et ![]() calculer :
calculer :
![]()
Dans ce qui suit, les nombres réels ![]() sont fixés (avec
sont fixés (avec ![]() ) tandis que
) tandis que ![]() est variable. On note
est variable. On note ![]() le sommet de la parabole d’équation
le sommet de la parabole d’équation ![]() Quel est le lieu de
Quel est le lieu de ![]() lorsque
lorsque ![]() varie ?
varie ?

Soient ![]() des entiers impairs. On suppose que l’équation
des entiers impairs. On suppose que l’équation ![]() possède deux solutions réelles. Montrer que celles-ci sont irrationnelles.
possède deux solutions réelles. Montrer que celles-ci sont irrationnelles.
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

