Manipulation de sommes à l'aide du symbole ∑

La manipulation de sommes, via le symbole $\Sigma$ (sigma), repose sur un petit nombre de règles. Cet article a pour objet de les énumérer et d’en donner des exemples d’utilisation, sans aucune prétention à l’originalité.

Pour vous entraîner à manier correctement cette écriture et les techniques associées, je vous suggère d’aller jeter un œil aux exercices accessibles depuis cette page.

Pour commencer, interrogeons-nous sur l’intérêt de la notation $\Sigma.$

1 – Abandon des points de suspension

En lisant la formule

$1+2+3+\cdots+10$

chacun comprend instantanément de quoi il retourne : pour calculer cette expression, on doit ajouter les entiers naturels de 1 jusqu’à 10. L’usage des points de suspension ne semble pas constituer, en l’occurrence, un obstacle à la compréhension.

Même chose pour :

$1+4+9+16+25+\cdots+625$

On devine aisément qu’il s’agit de la somme des carrés des entiers de 1 à 25.

Mais dans le cas de :

$1+0+3+4+9+12+19+24+\cdots+5001$

on ne voit pas, même après un certain délai de réflexion, ce que cachent les points de suspension.

Pourtant, ces nombres n’ont pas été choisis au hasard. Ce sont les premiers termes de la suite définie par la formule :

$u_{n}=\left\lfloor \frac{n^{2}+1}{2}\right\rfloor +\left(-1\right)^{n}$

où $\displaystyle{\left\lfloor X\right\rfloor}$ désigne la partie entière (par défaut) du réel $X.$ En effet :

$\begin{eqnarray*}u_{0}=\left\lfloor \frac{1}{2}\right\rfloor +\left(-1\right)^{0}=1\\u_{1}=\left\lfloor 1\right\rfloor +\left(-1\right)^{1}=0\\u_{2}=\left\lfloor \frac{5}{2}\right\rfloor +\left(-1\right)^{2}=3\\u_{3}=\left\lfloor 5\right\rfloor +\left(-1\right)^{3}=4\\u_{4}=\left\lfloor \frac{17}{2}\right\rfloor +\left(-1\right)^{4}=9\end{eqnarray*}$

et ainsi de suite…
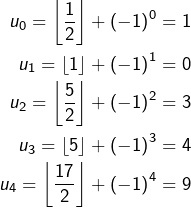
On pourrait donc penser que les points de suspension peuvent être utilisés, à condition qu’il n’existe aucun doute quant à l’identité de la suite sous-jacente. Mais ce n’est pas aussi simple…

Par exemple, si l’on pose pour tout entier $n\geqslant1$ :

$t_{n}=n+\left\lfloor \frac{n}{6}\right\rfloor$

les premiers termes de la suite $\left(t_{n}\right)_{n\geqslant1}$ sont :

$\begin{eqnarray*}t_{1}=1+\left\lfloor \frac{1}{6}\right\rfloor =1\\t_{2}=2+\left\lfloor \frac{1}{3}\right\rfloor =2\\t_{3}=3+\left\lfloor \frac{1}{2}\right\rfloor =3\\t_{4}=4+\left\lfloor \frac{2}{3}\right\rfloor =4\\t_{5}=5+\left\lfloor \frac{5}{6}\right\rfloor =5\end{eqnarray*}$

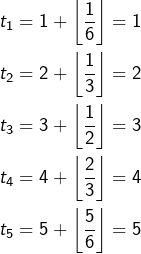
Mais attention :

$t_{6}=6+\left\lfloor 1\right\rfloor =7\qquad\text{(et non pas }6)$

Donc, lorsqu’on écrit :

$1+2+3+4+5+\cdots+10$

pourquoi ne s’agirait-il pas, après tout, de la somme des neufs premiers termes de la suite $\left(t_{n}\right)_{n\geqslant1}$ ?

Ceci montre la nécessité d’une notation totalement explicite, qui élimine toute ambiguïté.
On abandonne donc les points de suspension et on adopte la notation $\Sigma.$

2 – Le symbole ∑

Etant donnée une liste $\left(u_{k}\right)_{1\leqslant k\leqslant n}$ de nombres réels (ou, plus généralement, complexes), on note :

$\sum_{k=1}^{n}u_{k}$

pour désigner ce qu’on aurait noté jusque là : $u_{1}+\cdots+u_{n}$ . Cette formule se lit :

« somme, pour $k$ variant de 1 jusqu’à n, de u indice k ».

La symbole $k$ est l’indice de sommation.

Il est essentiel de comprendre que la somme ne dépend absolument pas de $k.$ Pour cette raison, ce symbole est qualifié de « muet ». Concrètement, cela signifie qu’on peut le remplacer par n’importe quel autre symbole… qui ne soit pas déjà utilisé dans le contexte du calcul !

Par exemple, étant donnés $n\in\mathbb{N}^{\star}$ et $\theta\in\mathbb{R},$ la somme :

$e^{\alpha+i\theta}+e^{2\alpha+i\theta}+e^{3\alpha+i\theta}+\cdots+e^{n\alpha+i\theta}$

peut être notée :

$\sum_{k=1}^{n}e^{k\alpha+i\theta}$

mais certainement pas :

$\sum_{i=1}^{n}e^{i\alpha+i\theta}$

puisque le symbole $i$ serait utilisé pour désigner deux choses différentes !!

Revenons au cas général. Au lieu de la notation ${\displaystyle \sum_{k=1}^{n}u_{k}},$ on peut utiliser l’une des deux variantes suivantes :

$\sum_{1\leqslant k\leqslant n}u_{k}\qquad\text{et}\qquad\sum_{k\in\llbracket1,n\rrbracket}u_{k}$

le symbole $\llbracket1,n\rrbracket$ désignant l’ensemble des entiers compris entre 1 et n (inclusivement).

L’écriture $\sum_{k\in\llbracket1,n\rrbracket}u_{k}$ se généralise facilement en $\sum_{i\in I}u_{i}$ où I est un ensemble fini et non vide (et où, pour tout $i\in I,$ $u_{i}$ désigne un nombre complexe).

Notons que, dans l’écriture ${\displaystyle \sum_{i\in I}u_{i}},$ rien n’indique la manière dont les termes sont additionnés. Mais c’est sans importance, puisque l’addition des nombres complexes est une opération commutative et associative. La commutativité permet de modifier l’ordre des termes sans affecter le total, tandis que l’associativité dit que les différents parenthésages possibles sont équivalents.

Une manière plus aboutie d’exprimer l’équivalence des différents parenthésages est la suivante.
Si l’on partitionne I en $p$ sous-ensembles $I_{1},\cdots,I_{p}$ (ce qui veut dire que les $I_{k}$ sont non vides, deux à deux disjoints et que leur union est I), alors (formule générale d’associativité) :

$\sum_{i\in I}u_{i}=\sum_{k\in\llbracket1,p\rrbracket}\left(\sum_{i\in I_{k}}u_{i}\right)$

Nous verrons à la section 7 une conséquence pratique importante de cette formule : l’interversion de sommes doubles sur des domaines de sommation rectangulaires ou triangulaires.

Ajoutons que, par convention, une somme de nombres complexes indexée par l’ensemble vide est nulle. Cette convention a le mérite de maintenir vraie la formule générale d’associativité, même si certains sous-ensembles $I_{k}$ sont vides.

Passons maintenant aux règles utilisées en pratique pour manipuler des sommes.

3 – Séparer / Fusionner

L’ordre des termes étant sans importance pour le calcul d’une somme, on voit que si $x_{1},\cdots,x_{n}$ et $y_{1},\cdots,y_{n}$ sont des nombres complexes quelconques, alors :

$\boxed{\sum_{i=1}^{n}\left(x_{i}+y_{i}\right)=\sum_{i=1}^{n}x_{i}+\sum_{i=1}^{n}y_{i}}$

Les parenthèses sont recommandées, pour ne pas dire indispensables ! Par exemple :

$\sum_{i=1}^{3}\left(i+1\right)=\left(1+1\right)+\left(2+1\right)+\left(3+1\right)=9$

tandis que, par défaut :

$\sum_{i=1}^{3}i+1$

s’interprète en :

$\left(\sum_{i=1}^{3}i\right)+1=7$

Mais revenons à la dernière égalité encadrée. Lorsqu’on la parcourt de gauche à droite, on dit qu’on sépare la somme en deux. Et lorsqu’on la parcourt de droite à gauche, on dit qu’on fusionne les deux sommes en une seule.

Il est nécessaire, pour la fusion, que les deux ensembles d’indices coïncident. Si tel n’est pas le cas, on peut éventuellement s’y ramener en effectuant une ré-indexation dans l’une des deux sommes : je ne vous ai pas encore parlé de ré-indexation, mais nous verrons cela un peu plus loin (cf. section 5).

4 – Développer / Factoriser

La formule bien connue de distributivité se généralise sans effort (simple récurrence) pour donner ceci :
si $x_{1},\cdots,x_{n}$ et $\lambda$ sont des nombres complexes, alors

$\boxed{\sum_{i=1}^{n}\lambda x_{i}=\lambda\sum_{i=1}^{n}x_{i}}$

Lorsqu’on parcourt cette égalité de gauche à droite, on dit qu’on met $\lambda$ en facteur dans la somme. Et lorsqu’on la parcourt de droite à gauche, on dit qu’on développe, ou qu’on distribue $\lambda$ sur la somme.

Et attention à l’erreur du débutant : pour avoir le droit de factoriser par $\lambda,$ encore faut-il que ce coefficient $\lambda$ soit indépendant de l’indice de sommation.

L’exemple qui suit est repris en détail dans la vidéo Calcul de Sommes, Episode 1. Si vous connaissez les propriétés des coefficients binomiaux, vous savez sans doute que pour tout couple d’entiers $\left(n,k\right)$ vérifiant $1\leqslant k\leqslant n$ :

$k\binom{n}{k}=n\binom{n-1}{k-1}$

Cette relation est appelée parfois « formule du pion ». Un exercice classique consiste à demander le calcul de la somme :

$S_{n}=\sum_{k=1}^{n}k\binom{n}{k}$

Mettre $k$ en facteur dans cette somme serait monstrueux ! Il n’y a d’ailleurs, sous cette forme, rien à mettre en facteur. Mais en écrivant plutôt :

$S_{n}=\sum_{k=1}^{n}n\binom{n-1}{k-1}$

on peut factoriser par $n,$ ce qui conduit à :

$S_{n}=n\sum_{k=1}^{n}\binom{n-1}{k-1}$

Pour finir, la somme des termes de la $\left(n-1\right)-$ ème ligne du triangle de Pascal est égale à $2^{n-1}$ , donc :

$\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=1}^nk\binom{n}{k}=n\,2^{n-1}}$}$

5 – Changer d’indice

Changer d’indice dans (ou : ré-indexer) une somme consiste simplement à en re-numéroter les termes. Par exemple, la somme $S=x_{1}+x_{2}+x_{3}+x_{4}$ peut s’écrire :

$S=\sum_{i=1}^{4}x_{i}$

mais aussi :

$S=\sum_{j=0}^{3}x_{j+1}$

ou encore :

$S=\sum_{k=2}^{5}x_{k-1}$

Pour passer de la première écriture à la seconde, on pose $j=i-1$ et pour passer de la première à la troisième, on pose $k=i+1.$

Ces exemples sont très simples : on a ré-indexé la somme en décalant l’ancien indice d’une unité. On est parfois conduit à effectuer d’autres types de ré-indexation. Par exemple, si l’on considère :

$S=\sum_{i=0}^{n}x_{i}$

et qu’on pose $j=n-i,$ on obtient :

$S=\sum_{j=0}^{n}x_{n-j}$

Les changements d’indice du type $j=i+c$ ou bien $j=-i+c$ (où l’entier $c$ est fixé) sont assez fréquents.

D’une manière plus générale, étant donnés deux ensembles finis $I$ et $J$ , si $f:I\rightarrow J$ est bijective et si $\left(x_{j}\right)_{j\in J}$ est une famille de nombres complexes indexée par $J,$ alors :

$\sum_{i\in I}x_{f\left(i\right)}=\sum_{i\in J}x_{j}$

On dit qu’on passe du membre de gauche à celui de droite en posant $j=f\left(i\right).$

Voyons un exemple de ce mécanisme, en considérant un groupe fini $\left(G,\times\right)$ et un morphisme $\Phi$ de ce groupe vers le groupe $\left(\mathbb{C}^{\star},\times\right)$ des nombres complexes non nuls. Calculons la somme :

$S=\sum_{g\in G}\Phi\left(g\right)$

Si $\Phi$ est le morphisme constant (c’est-à-dire $\Phi\left(g\right)=1$ pour tout $g\in G$ ), alors $S=\text{card}\left(G\right)$ .

Et sinon, il existe $h\in G$ tel que $\Phi\left(h\right)\neq1.$ L’application $G\rightarrow G,\thinspace\gamma\rightarrow h\gamma$ étant bijective (c’est ce qu’on appelle une translation du groupe $G)$ , on peut effectuer dans la somme le changement d’indice défini par $g=h\gamma$ , ce qui donne :

$S=\sum_{\gamma\in G}\Phi\left(h\gamma\right)=\sum_{\gamma\in G}\Phi\left(h\right)\thinspace\Phi\left(\gamma\right)=\Phi\left(h\right)\thinspace S$

et donc :

$\left(1-\Phi\left(h\right)\right)S=0$

soit finalement : $S=0.$ En résumé :

$\boxed{\sum_{g\in G}\Phi\left(g\right)=\left\{\begin{array}{cc}\text{card}(G) & \text{ si }\forall g\in G,\,\Phi(g)=1\\0 & \text{sinon}\end{array}\right.}$

6 – Sommations télescopiques

Etant donnés un entier $n\geqslant1$ et des nombres complexes $t_{0},\cdots,t_{n}$ l’expression :

$S=\sum_{k=0}^{n-1}\left(t_{k}-t_{k+1}\right)$

se simplifie en $S=t_{0}-t_{n}.$

Cela se comprend en écrivant explicitement les quelques premiers termes et les quelques derniers (le calcul qui suit suppose $n\geqslant3$ ) :

$\begin{eqnarray*}S & = & \left(t_{0}-t_{1}\right)+\\& & \left(t_{1}-t_{2}\right)+\\& & \left(t_{2}-t_{3}\right)+\\& & \cdots\\& & \left(t_{n-3}-t_{n-2}\right)\\& & \left(t_{n-2}-t_{n-1}\right)\\& & \left(t_{n-1}-t_{n}\right)\end{eqnarray*}$

On voit très bien que les termes se compensent deux à deux, à l’exception de $t_{0}$ et $-t_{n},$ qui sont les deux “survivants” …

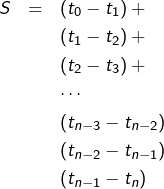
On dit qu’une telle sommation est “télescopique”. Cette appellation fait sans doute référence à ce qui se passe lorsqu’on replie une lunette télescopique (cf. figure ci-dessous) : seules les extrémités restent visibles !

La formule

$\boxed{\sum_{k=0}^{n-1}\left(t_{k}-t_{k+1}\right)=t_{0}-t_{n}}$

peut être justifiée proprement de deux façons :

soit par récurrence sur n,
soit en séparant en deux sommes, puis en ré-indexant l’une d’elles.

Les choses deviennent intéressantes lorsque la sommation n’apparaît pas, au premier coup d’œil, comme étant télescopique …

Par exemple, si l’on pose pour tout entier $n\geqslant2$ :

$\boxed{S_{n}=\sum_{k=2}^{n}\frac{1}{k\left(k-1\right)}}$

On peut astucieusement écrire, pour tout $k\geqslant2$ :

$\frac{1}{k\left(k-1\right)}=\frac{1}{k-1}-\frac{1}{k}$

Il est alors clair que :

$\fcolorbox{black}{myBlue}{$\displaystyle{S_{n}=1-\frac{1}{n}}$}$

Autre exemple, considérons pour tout $n\geqslant1$ :

$\boxed{T_{n}=\sum_{k=1}^{n}\frac{k}{\left(k+1\right)!}}$

En remarquant que, pour tout $k\geqslant1$ :

$\begin{eqnarray*}\frac{k}{\left(k+1\right)!} & = & \frac{\left(k+1\right)-1}{\left(k+1\right)!}\\& = & \frac{1}{k!}-\frac{1}{\left(k+1\right)!}\end{eqnarray*}$

on voit que :

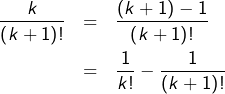
$\fcolorbox{black}{myBlue}{$\displaystyle{T_{n}=1-\frac{1}{\left(n+1\right)!}}$}$

Dernier exemple, ajoutons les premiers termes de la suite de Fibonacci. On rappelle que la suite de Fibonacci $\left(F_{n}\right)_{n\in\mathbb{N}}$ est définie par les relations :

$F_{0}=0\qquad F_{1}=1$

$\forall n\in\mathbb{N}^{\star},\thinspace F_{n+1}=F_{n}+F_{n-1}$

Pour calculer explicitement la somme :

$\boxed{V_{n}=\sum_{k=1}^{n}F_{k}}$

on peut simplement la ré-écrire :

$V_{n}=\sum_{k=1}^{n}\left(F_{k+1}-F_{k-1}\right)$

Cette fois le « télescopage » se fait, non pas entre un terme et son voisin immédiat, mais plutôt de deux en deux. Le plus simple, pour ne pas se prendre les pieds dans le tapis, consiste à écrire :

$V_{n}=\sum_{k=1}^{n}\left(F_{k+1}-F_{k}\right)+\sum_{k=1}^{n}\left(F_{k}-F_{k-1}\right)$

de sorte que :

$V_{n}=F_{n+1}-F_{1}+F_{n}-F_{0}$

soit finalement :

$\fcolorbox{black}{myBlue}{$\displaystyle{V_n=F_{n+2}-1}$}$

7 – Intervertir deux sommes

Considérons deux entiers $n,p\geqslant1$ ainsi que $np$ nombres complexes $a_{i,j}$ , avec $1\leqslant i\leqslant n$ et $1\leqslant j\leqslant p\right$ . Posons alors :

$S=\sum_{\left(i,j\right)\in\llbracket1,n\rrbracket\times\llbracket1,p\rrbracket}a_{i,j}$

Comme expliqué à la section 2, cette notation a un sens, car peu importe l’ordre dans lequel les termes sont additionnés et peu importe le parenthésage utilisé.

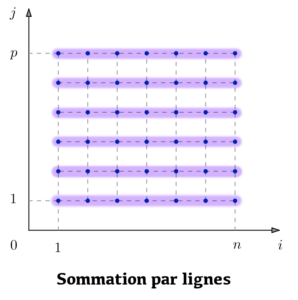
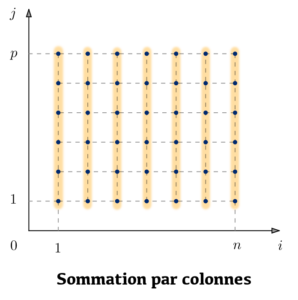
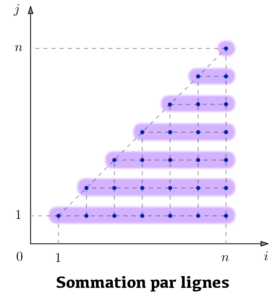
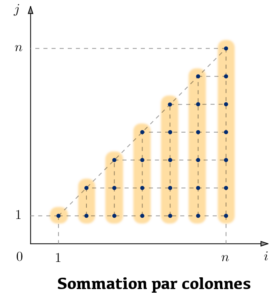
En particulier, l’ensemble $\llbracket1,n\rrbracket\times\llbracket1,p\rrbracket$ peut être partitionné «en lignes» ou bien «en colonnes», comme suggéré par l’illustration ci-dessous :

Ceci conduit à la formule suivante, appelée « formule d’interversion pour un domaine de sommation rectangulaire » :

( $\heartsuit$ ) $\boxed{\sum_{j=1}^{p}\left(\sum_{i=1}^{n}\,a_{i,j}\right)=\sum_{i=1}^{n}\left(\sum_{j=1}^{p}\,a_{i,j}\right)}$

Le cas d’un domaine de sommation triangulaire, est tout aussi important en pratique.
Par exemple, si l’on considère :

$\sum_{\left(i,j\right)\in T}a_{i,j}\qquad\text{avec }T=\left\{ \left(i,j\right)\in\mathbb{N}^{2};\thinspace1\leqslant j\leqslant i\leqslant n\right\}$

on peut, à nouveau, sommer «en lignes» ou bien «en colonnes» :

Et voici la formule correspondante :

( $\spadesuit$ ) $\boxed{\sum_{j=1}^{n}\,\left(\sum_{i=j}^{n}\,a_{i,j}\right)=\sum_{i=1}^{n}\,\left(\sum_{j=1}^{i}\,a_{i,j}\right)}$

Donnons deux exemples de calcul faisant intervenir les formules $\left(\heartsuit\right)$ et $\left(\spadesuit\right)$ .

Exemple 1

Etant donnés $n\in\mathbb{N}^{\star}$ et $p\in\mathbb{N}$ , on pose :

$\boxed{S_{n,p}=\sum_{k=1}^{n}\,k^{p}}$

Il est connu que :

$S_{n,1}=\frac{n\left(n+1\right)}{2};\quad S_{n,2}=\frac{n\left(n+1\right)\left(2n+1\right)}{6};\quad S_{n,3}=\frac{n^{2}\left(n+1\right)^{2}}{4}$

Comment obtenir ces formules de façon « naturelle » ? Une approche consiste à calculer de deux manières l’expression :

$W_{n,p}=\sum_{k=1}^{n}\left[\left(k+1\right)^{p+1}-k^{p+1}\right]$

D’une part, la sommation est télescopique :

( $\clubsuit$ ) $W_{n,p}=\left(n+1\right)^{p+1}-1$

et d’autre part, d’après la formule du binôme :

$W_{n,p}=\sum_{k=1}^{n}\left[\sum_{j=0}^{p}\binom{p+1}{j}k^{j}\right]$

Après interversion des sommes (le domaine est rectangulaire) et mise en facteur du coefficient binomial, on obtient :

( $\diamondsuit$ ) $W_{n,p}=\sum_{j=0}^{p}\left[\binom{p+1}{j}\sum_{k=1}^{n}k^{j}\right]=\sum_{j=0}^{p}\binom{p+1}{j}S_{n,j}$

d’où, en confrontant les égalités $\left(\clubsuit\right)$ et $\left(\diamondsuit\right)$ , la formule de récurrence « forte » :

$\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{j=0}^{p}\binom{p+1}{j}S_{n,j}=\left(n+1\right)^{p+1}-1}$}$

Si des formules explicites sont connues pour chacune des sommes $S_{n,0}$ , $S_{n,1}$ , etc …, $S_{n,p-1}$ , alors cette égalité permet de calculer $S_{n,p}$ .

Par exemple, connaissant les formules :

$S_{n,0}=n,\qquad S_{n,1}=\frac{n\left(n+1\right)}{2},\qquad S_{n,2}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

on obtient en appliquant ce qui précède (avec $p=3$ ) :

$\binom{4}{0}S_{n,0}+\binom{4}{1}S_{n,1}+\binom{4}{2}S_{n,2}+\binom{4}{3}S_{n,3}=\left(n+1\right)^{4}-1$

c’est-à-dire :

$n+2n\left(n+1\right)+n\left(n+1\right)\left(2n+1\right)+4\thinspace S_{n,3}=\left(n+1\right)^{4}-1$

d’où, après quelques petits calculs pas bien méchants :

$\fcolorbox{black}{myBlue}{$\displaystyle{S_{n,3}=\frac{n^{2}\left(n+1\right)^{2}}{4}}$}$

Exemple 2

Pour tout entier $n\geqslant1$ , on note classiquement $H_{n}$ le n-ème « nombre harmonique » :

$H_{n}=\sum_{k=1}^{n}\frac{1}{k}$

Il existe une foule de choses à savoir au sujet de la suite $\left(H_{n}\right)_{n\geqslant1}$ , mais nous porterons notre attention sur la formule de récurrence suivante :

( $\star\star$ ) $H_{n+1}=1+\frac{1}{n+1}\sum_{j=1}^{n}H_{k}$

Elle se démontre à l’aide de $\left(\spadesuit\right)$ :

$\begin{eqnarray*}\sum_{k=1}^{n}H_{k} & = & \sum_{k=1}^{n}\left(\sum_{j=1}^{k}\frac{1}{j}\right)\\& = & \sum_{j=1}^{n}\left(\sum_{k=j}^{n}\frac{1}{j}\right)\\& = & \sum_{j=1}^{n}\frac{n-j+1}{j}\\& = & \left(n+1\right)H_{n}-n\\& = & \left(n+1\right)\left(H_{n+1}-1\right)\end{eqnarray*}$

Avec cette formule $\left(\star\star\right)$ , on retrouve la divergence de la suite $\left(H_{n}\right)_{n\geqslant1}$ . En effet, si cette suite convergeait vers un réel $\lambda$ , on aurait d’après le lemme de Cesàro :

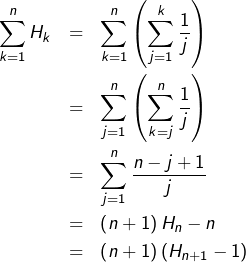
$\lim_{n\rightarrow\infty}\frac{1}{n+1}\sum_{j=1}^{n}H_{k}=\lambda$

et donc, en passant à la limite dans $\left(\star\star\right)$ , il en résulterait que $\lambda=\lambda+1$ , ce qui est absurde !

Pour un exemple du même style, mais plus élaboré, voir le challenge 35

8 – Et pour les produits ?

L’analogue du symbole $\Sigma$ pour représenter un produit est le symbole $\Pi$ (il s’agit de la lettre majuscule grecque « pi »).

Si $a_1,\ldots,a_n$ sont des nombres réels ou complexes, leur produit est donc noté :

$\prod_{k=1}^na_k$

Ce symbole se manipule essentiellement de la même manière que le symbole $\Sigma$ . Par exemple, la formule de fusion / séparation s’écrit maintenant :

$\prod_{k=1}^na_kb_k=\left(\prod_{k=1}^na_k\right)\,\left(\prod_{k=1}^nb_k\right)$

En particulier, si $b_k=\lambda$ pour tout $k$ , cette égalité prend la forme :

$\prod_{k=1}^n\lambda a_k=\lambda^n\left(\prod_{k=1}^na_k\right)$

l’erreur classique consistant à oublier l’exposant $n$ .

Tout comme les sommes (cf. section 6), les produits peuvent se télescoper. La formule de base est :

$\prod_{k=0}^{n-1}\frac{a_k}{a_{k+1}}=\frac{a_0}{a_n}$

où $a_1,\ldots, a_n$ sont tous supposés non nuls.

Voyons pour terminer trois petits exemples de calculs faisant intervenir la notation $\Pi$ :

Exemple 1

Pour tout $n\in\mathbb{N}^\star$ et pour tout $q\in\mathbb{C}$ :

$\prod_{k=1}^nq^k=q^{n(n+1)/2}$

En effet, un produit de puissances d’un même nombre $q$ est égal à $q^s$ où $s$ désigne la somme des exposants. Or, nous savons que $\displaystyle{\sum_{k=1}^nk=\frac{n(n+1)}{2}}$ .

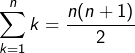Exemple 2

Posons pour tout entier $n\geqslant1$ :

$P_n=\prod_{k=1}^n\frac{\sqrt k}{1+\sqrt k}$

et montrons que :

$\lim_{n\to+\infty}P_n=0$

Il est facile de voir que, pour tout $k\geqslant1$ :

$\frac{\sqrt k}{1+\sqrt k}\leqslant\frac{k}{1+k}$

par exemple en remarquant que l’application $t\mapsto\frac{t}{1+t}$ est croissante sur $[0,+\infty[$ .

Il s’ensuit que :

$P_n\leqslant\prod_{k=1}^n\frac{k}{1+k}=\frac{1}{1+n}$

d’où la conclusion.

Exemple 3

Cherchons une expression simplifiée pour :

$Q_n=\prod_{k=1}^n\frac{k!}{k^{n-k+1}}$

En calculant ceci pour de petites valeurs de $n$ , on trouve invariablement 1. On conjecture alors que $\forall n\in\mathbb{N}^\star,\,Q_n=1$ , ce qu’on prouve par récurrence sans trop de problème (non détaillé).

Une autre façon d’aborder cette question consiste à écrire $\displaystyle{\prod_{k=1}^nk!}$ comme un produit double (un produit de produits) puis à intervertir les deux produits (tout comme on sait intervertir deux sommes : cf. section 7) :

$\prod_{k=1}^nk!=\prod_{k=1}^n\left(\prod_{j=1}^kj\right)\underset{\star}{=}\prod_{j=1}^n\left(\prod_{k=j}^nj\right)=\prod_{j=1}^nj^{n-j+1}$

ce qui prouve bien que $Q_n=1$ .

L’égalité repérée par un $\star$ résulte d’une interversion sur un domaine triangulaire.

Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article

Cet article a 4 commentaires

khalfa sarah 25 Avr 2024 Répondre

wow merci beaucoup pour ce contenu de qualité, cela m a énormément aidé ! bonne continuation à vous : )
herve laurent 28 Sep 2018 Répondre

la somme de -n à n de (k+1)
1. René Adad 28 Sep 2018 Répondre
  
  Si $n\geqslant1$ , alors :
  
  $\sum_{k=-n}^n(k+1)=\sum_{k=-n}^nk+\sum_{k=-n}^n1$
  
  or la première somme est nulle (regrouper le premier terme avec le dernier, le second avec l’avant-dernier, etc…) et la seconde vaut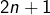 $2n+1$ puisqu’elle comporte 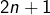$2n+1$ termes tous égaux à 1. Bref :
  
  $\boxed{\sum_{k=-n}^n(k+1)=2n+1}$
René Adad 21 Nov 2017 Répondre

Il va être difficile de répondre, à part pour dire qu’une telle somme est un entier… Merci de préciser quelle somme vous souhaitez calculer.