Lettre M

MONOTONE (théorème de la limite)

On peut énoncer deux théorèmes de la limite monotone (TLM) : l’un concerne les suites réelles, l’autre les applications d’un intervalle (non trivial) dans $\mathbb{R}.$ Tous deux racontent essentiellement la même histoire et reposent sur l’existence, pour toute partie non vide et majorée de $\mathbb{R},$ d’une borne supérieure.

TLM pour les suites

Si $u$ est une suite réelle croissante et majorée, alors $u$ est convergente.

Ce résultat est particulièrement précieux parce qu’il permet d’établir la convergence d’une suite sans qu’il soit nécessaire d’en connaître à l’avance la limite (contrairement à ce qui se passe lorsqu’on revient à la définition de la convergence). On reconnaît là un trait caractéristique du critère de Cauchy.

Bien entendu, la conclusion persiste en supposant $u$ décroissante et minorée. Elle persiste aussi en supposant seulement la croissance (ou la décroissance) à partir d’un certain rang.

Exemple

La suite de terme général :

$u_{n}=\sum_{k=0}^{n}\frac{1-e^{-k}}{k^{2}+k+1}$

est croissante, puisque pour tout $n\in\mathbb{N}^{\star}$ :

$u_{n}-u_{n-1}=\frac{1-e^{-n}}{n^{2}+n+1}\geqslant0$

Elle est de plus majorée, car pour tout $n\in\mathbb{N}^{\star}$ :

$\begin{eqnarray*}u_{n} & \leqslant & 1+\sum_{k=1}^{n}\frac{1}{k\left(k+1\right)}\\& = & 1+\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)\\& = & 2-\frac{1}{n+1}\\& \leqslant & 2\end{eqnarray*}$

Cette suite est donc convergente.

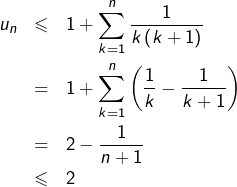
TLM pour les fonctions (version 1)

Si $a\in\mathbb{R}$ et $f:\left[a,+\infty\right[\rightarrow\mathbb{R}$ est croissante (resp. décroissante) et majorée (resp. minorée), alors $f$ admet en $+\infty$ une limite finie.

Dans cette vidéo, cette version est utilisée pour montrer que :

$\lim_{x\rightarrow+\infty}\frac{\ln\left(x\right)}{x}=0$

TLM pour les fonctions (version 2)

Si $I$ est un intervalle non trivial et si $f:I\rightarrow\mathbb{R}$ est monotone, alors $f$ admet :

une limite finie à gauche et à droite en tout point intérieur à $I$
une limite finie à gauche en tout 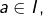$a\in I,$ autre que son éventuelle extrémité gauche
une limite finie à droite en tout $a\in I,$ autre que son éventuelle extrémité droite

Remarque

Dans le cas où $I=\left[a,b\right]$ avec $a<b$ , l’existence d’une limite finie à gauche en tout point de $\left]a,b\right]$ et d’une limite finie à droite en tout point de $\left[a,b\right[$ n’est pas propre aux applications monotones. Elle est caractéristique d’une classe plus vaste, celle des applications réglées. Par définition, f est dite réglée sur $\left[a,b\right]$ lorsqu’elle est limite uniforme sur ce segment d’une suite d’applications en escalier.

Exemple d’utilisation

Si $I,J$ sont deux intervalles non triviaux et si $f:I\rightarrow J$ est monotone et surjective, alors $f$ est continue.

Preuve (cliquer pour déplier / replier)

Quitte à changer $f$ en $-f$ , on peut supposer $f$ croissante Si $f$ présentait une discontinuité en $a$ intérieur à $I,$ on aurait :

$G\underset{\text{def}}{=}\lim_{x\rightarrow a^{-}}f\left(x\right)<f\left(a\right)\qquad\text{ou}\qquad f\left(a\right)<\lim_{x\rightarrow a^{+}}f\left(x\right)\underset{\text{def}}{=}D$

(le ou étant inclusif). Dans le premier cas, aucun élément de $\left]G,f\left(a\right)\right[$ ne possèderait d’antécédent, bien qu’appartenant à $J$ (voir la définition d’un intervalle) : ceci contredit l’hypothèse de surjectivité de $f.$ Même type de contradiction dans le second cas. Et argument similaire si $a$ est une extrémité de $I.$

MOYENNES

Moyenne pondérée

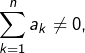Etant donné un entier $n\geqslant2,$ si $x_{1},\cdots,x_{n}$ et $a_{1},\cdots,a_{n}$ sont des nombres réels tels que $\sum_{k=1}^{n}a_{k}\neq0,$ on définit la moyenne de $x_{1},\cdots,x_{n}$ pondérée par $a_{1},\cdots,a_{n}$ :

( $\star$ ) $M=\frac{{\displaystyle \sum_{k=1}^{n}a_{k}x_{k}}}{{\displaystyle \sum_{k=1}^{n}a_{k}}}$

C’est avec cette formule qu’un lycéen peut calculer la moyenne de ses notes : les $x_{k}$ sont les notes et les $a_{k}$ sont les coefficients.

On reconnaît un cas particulier de la notion de barycentre.

Moyennes A, G et H

Si $x_{1},\cdots,x_{n}$ sont des réels strictement positifs, on définit leurs moyennes …

➢ Arithmétique :

$\boxed{\displaystyle{A=\frac{1}{n}\sum_{k=1}^{n}x_{k}}}$

➢ Géométrique :

$\boxed{\displaystyle{G=\left(\prod_{k=1}^{n}x_{k}\right)^{1/n}}}$

➢ Harmonique :

$\boxed{H=\frac{n}{{\displaystyle \sum_{k=1}^{n}\frac{1}{x_{k}}}}}$

Noter que :

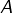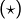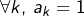$A$ correspond à une moyenne pondérée $\left(\star\right)$ avec $\forall k,\,a_{k}=1$ (isobarycentre).
$G$ est le nombre dont le logarithme est la moyenne arithmétique des logarithmes,
$H$ est le nombre dont l’inverse est la moyenne arithmétique des inverses.

On peut montrer que $H\leqslant G\leqslant A,$ en invoquant la convexité de la fonction exponentielle, mais il existe d’autres preuves ce résultat … Par exemple celle-ci.

Illustration dynamique

Dans l’animation ci-dessous, les moyennes $H,G,A$ sont calculés pour une douzaine de valeurs qui se promènent aléatoirement dans l’intervalle $\left]0,1\right]$ (en fait dans $\left]10^{-1},1\right]$ , pour des raisons esthétiques …). On peut interrompre / relancer l’animation en cliquant dans la fenêtre graphique.

On observe que les positions relatives de $H,G$ et $A$ restent stables.

Remarque de terminologie

L’expression moyenne arithmétique (respectivement : géométrique) est à rapprocher du fait que si $a,b,c>0$ sont trois termes consécutifs d’une suite arithmétique (resp. géométrique), alors $b$ est la moyenne arithmétique (resp. géométrique) de $a$ et $c.$

On définit de manière analogue la notion de suite harmonique : une suite $\left(h_{n}\right)_{n\geqslant0}$ de réels non nuls, dont chaque terme est la moyenne harmonique de ses deux voisins. Au lycée, on rencontre les notions de suites arithmétiques et de suites géométriques. Celle de suite harmonique semble ne pas avoir connu le même succès … Et ceci s’explique sans doute par le fait qu’en remplaçant chaque terme d’une telle suite par son inverse, on est aussitôt ramené à une suite arithmétique.

Exemple de suite harmonique : $\displaystyle{\left(\frac{1}{n}\right)_{n\geqslant1}}$

Signalons deux interprétations géométriques. L’une pour la moyenne
… géométrique de deux nombres positifs :

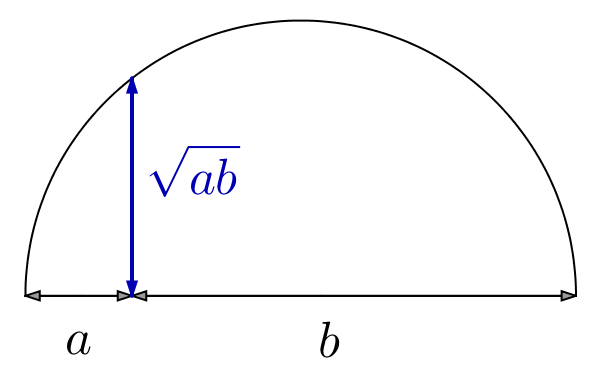
et l’autre, pour leur moyenne harmonique :

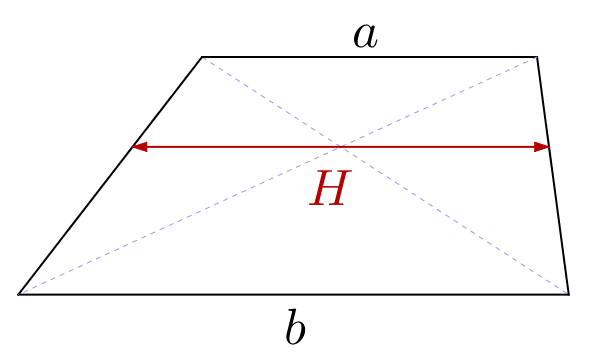
Les deux illustrations ci-dessus parlent d’elles-mêmes … mais encore faut-il prouver que les segments bleu et rouge ont bien les longueurs indiquées ! Exercice pour le lecteur 🙂

Proposition

Etant donnés $0<b<a,$ considérons les suites $\left(x_{n}\right)_{n\in\mathbb{N}}$ et $\left(y{n}\right)_{n\in\mathbb{N}}$ définies par :

$x_{0}=a\quad\text{et}\quad y_{0}=b$

et les formules de récurrence :

$\forall n\in\mathbb{N},\thinspace x_{n+1}=\frac{x_{n}+y_{n}}{2}\quad\text{et}\quad y_{n+1}=\sqrt{x_{n}y_{n}}$

Ces deux suites sont adjacentes. La première décroît, la seconde croît et elles convergent toutes les deux vers la moyenne arithmético-géométrique de $a,b,$ qu’on peut noter $\text{AGM}\left(a,b\right),$ et dont l’inverse est:

$\boxed{\frac{1}{\text{AGM}\left(a,b\right)}=\frac{2}{\pi}\int_{0}^{\pi/2}\frac{dt}{\sqrt{a^{2}\cos^{2}\left(t\right)+b^{2}\sin^{2}\left(t\right)}}}$

Ce résultat est attribué à Gauss et Legendre.

A l’entrée ADJACENTES (exemple 1) du lexique, on trouvera un scenario similaire, mais en un sens plus simple : deux suites construites en itérant des calculs de moyennes arithmétique et harmonique.

Dans la formule encadrée ci-dessus, apparaît encore une moyenne, mais pour une fonction cette fois :

Moyenne d’une fonction

Si $a<b$ et si $f:\left[a,b\right]\rightarrow\mathbb{R}$ est continue, on définit la valeur moyenne de $f$ :

$M_{f}=\frac{1}{b-a}\int_{a}^{b}f\left(t\right)\thinspace dt$

Ce réel peut s’interpréter comme la valeur qu’on doit donner à une fonction constante pour qu’elle possède la même intégrale que $f.$ Une conséquence du théorème des valeurs intermédiaires est l’existence d’un réel $c\in\left[a,b\right]$ tel que $M_{f}=f\left(c\right).$ C’est ce qu’on appelle la première formule de la moyenne pour les intégrales.

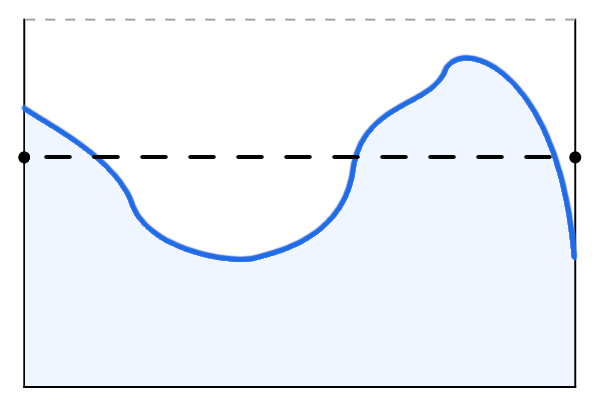
On peut s’en faire l’image mentale suivante. Imaginons un récipient de forme parallélépipédique, de profondeur faible devant sa largeur et sa hauteur :

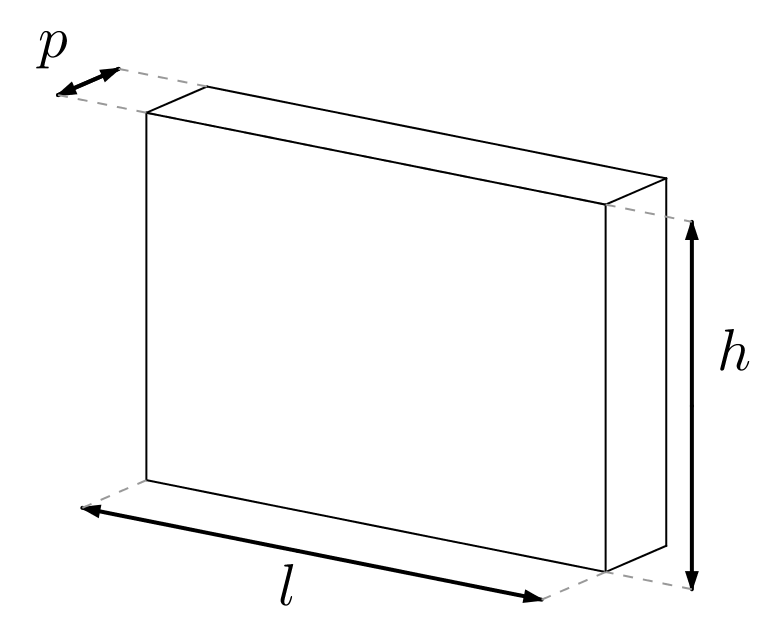
Après l’avoir rempli d’eau, voici ce qu’on peut voir si l’on secoue le récipient et ce qu’on verra après que le calme soit rétabli :

Le niveau de l’eau à l’équilibre indique la valeur moyenne de la « fonction ».

Noter que, d’après le théorème de convergence des sommes de Riemann, $M_{f}$ est la limite de la suite de terme général :

$\mu_{n}=\frac{1}{n}\sum_{k=0}^{n-1}f\left(a+\frac{k\left(b-a\right)}{n}\right)$

qui est justement la moyenne arithmétique des valeurs prises par $f$ aux points d’une subdivision régulière.

Partager cet article