Neuf énoncés d’exercices sur les séries numériques (fiche 01).

Soit ![]() une suite réelle telle que la série
une suite réelle telle que la série ![]() converge.
converge.
Etudier la nature de la série ![]()

Soit ![]() une suite de réels strictement positifs.
une suite de réels strictement positifs.
Montrer que les séries ![]() et
et ![]() sont de même nature.
sont de même nature.

Vrai ou Faux ?
Etant données trois suites réelles ![]()
![]() et
et ![]() vérifiant
vérifiant
![]()

Déterminer la nature de la série 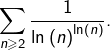

En observant que, pour tout ![]() :
:
![]()
prouver que la série 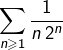 converge et admet
converge et admet ![]() pour somme.
pour somme.

En exploitant les calculs de l’exercice précédent et en rédigeant un (tout petit) programme informatique, trouver une valeur approchée de ![]() à
à ![]() près.
près.


Soit ![]() une suite de réels strictement positifs.
une suite de réels strictement positifs.
On suppose que :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\,\frac{\ln\left(\frac{1}{a_{n}}\right)}{\ln\left(n\right)}=\alpha\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d294177cb972f9898480205d11fd4e15_l3.png)
Montrer que si ![]() alors la série
alors la série ![]() et la série de Riemann
et la série de Riemann 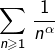 sont de même nature.
sont de même nature.
Que peut-on dire si ![]() ?
?

Calculer explicitement 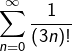

Montrer que la série 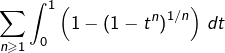 est convergente.
est convergente.
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions


bon chemin; après series doubles et un bon expose sur les familles sommables
merci