
Une des nombreuses facettes de la géométrie plane est l’étude des courbes : coniques, cubiques, cycloïdes, spirales … mais encore : développées / développantes, conchoïdes, strophoïdes, etc …
C’est une courbe en forme de huit, connue sous le nom de lemniscate de Bernoulli, qui fait l’objet du présent article. Le terme lemniscate semble provenir du latin lemniscus qui désigne un ruban. Cette terminologie a été choisie par Jacques Bernoulli (1654-1705), qui fut un mathématicien et un physicien suisse de premier plan.

1 – Les ovales de Cassini
Jean Dominique Cassini (1625-1712) était un astronome italien. On lui doit, entre-autres, la découverte de la grande tâche rouge de Jupiter, celle d’une zone sombre (connue depuis sous le nom de division de Cassini) au sein des anneaux de Saturne, ainsi que la découverte de Japet, Thétys, Dioné et Rhéa, quatre satellites de Saturne (les trois derniers sont visibles sur l’image ci-dessous, la petite flèche indiquant l’ombre de Thétys).
Dans le cadre de ses recherches sur les mouvements relatifs de la terre et du soleil, Cassini s’intéressa vers 1680 au problème suivant :
Une question de lieu géométrique
Déterminer les points du plan dont le produit des distances à deux points fixes est constant.
Etant donnés deux points distincts ![]() et
et ![]() du plan, ainsi qu’un nombre positif
du plan, ainsi qu’un nombre positif ![]() , notons
, notons ![]() l’ensemble des points
l’ensemble des points ![]() tels que :
tels que :
![]()
Un point ![]() appartient à
appartient à ![]() si, et seulement si :
si, et seulement si :
![]()
![]()
![]()
![]()
Les courbes algébriques ![]() sont connues sous le nom d’ovales de Cassini. L’illustration dynamique ci-dessous montre la déformation de
sont connues sous le nom d’ovales de Cassini. L’illustration dynamique ci-dessous montre la déformation de ![]() lorsque le paramètre
lorsque le paramètre ![]() varie (on a choisi
varie (on a choisi ![]() ) :
) :
Illustration dynamique
Utiliser le slider pour modifier la valeur de ![]() .
.
Lorsque le curseur est dans le cadre gris, on peut presser la touche :
- L pour choisir
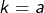 (l’ovale est alors une lemniscate),
(l’ovale est alors une lemniscate), - M pour montrer le point M , les segments MA et MB, ainsi que la valeur courante de la différence
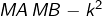 (qui s’annule lorsque M appartient à l’ovale).
(qui s’annule lorsque M appartient à l’ovale).
La courbe qui nous intéresse est obtenue pour ![]() seule valeur du paramètre pour laquelle l’origine appartient à
seule valeur du paramètre pour laquelle l’origine appartient à ![]() :
:
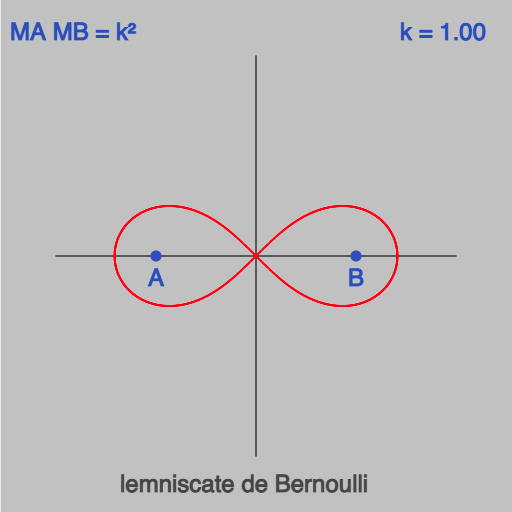
Jacques Bernoulli (1654-1705) étudia cette courbe. Il lui donna le nom de lemniscate et lui consacra un mémoire en 1694, dans Acta Eruditorum. C’est à Giovanni Fagnano (1715-1797) que revient le mérite d’avoir observé (vers 1750) que la lemniscate de Bernoulli est une ovale de Cassini particulière.
Jacques Bernoulli est issu d’une famille qui compta plusieurs mathématiciens très prolifiques, parmi lesquels son frère Jean et ses neveux Nicolas, Daniel et Jean. On lui doit une célèbre suite de nombres, des polynômes, une loi de probabilité, des équations différentielles d’un type particulier et bien d’autres choses …

2 – Paramétrages usuels
Conformément à ce qui a été vu plus haut, nous appelons lemniscate une courbe admettant, dans un repère orthonormal convenable et pour un certain ![]() une équation de la forme :
une équation de la forme :
![]()
En coordonnées polaires, cette équation devient :
![]()
On peut vérifier que la courbe paramétrée par les équations :
![Rendered by QuickLaTeX.com \[\boxed{\left\{ \begin{array}{ccc}x & = & {\displaystyle \frac{t}{1+t^{4}}}\\\\y & = & {\displaystyle \frac{t^{3}}{1+t^{4}}}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9bc7c79884e3d8957d5c39e3f95e5448_l3.png)
Afin de prouver qu’il s’agit bien d’une lemniscate (après tout, tout ce qui brille n’est pas or …), on peut effectuer une rotation des axes en posant :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}X & = & \frac{\sqrt{2}}{2}\left(x+y\right)\\\\Y & = & \frac{\sqrt{2}}{2}\left(-x+y\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6094510189c21a13929787f837a59bd2_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}X & = & {\displaystyle \frac{\sqrt{2}}{2}\frac{t+t^{3}}{1+t^{4}}}\\\\Y & = & {\displaystyle \frac{\sqrt{2}}{2}\frac{-t+t^{3}}{1+t^{4}}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9647d46eabeb39f11d84b1428314a19a_l3.png)
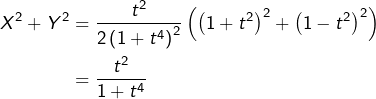
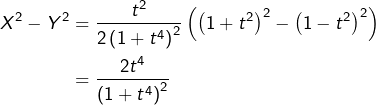
![]()
Ceci montre que la lemniscate est une courbe unicursale, c’est-à-dire admettant une représentation paramétrique de la forme ![]()
![]() où
où ![]() sont des fractions rationnelles.
sont des fractions rationnelles.
Plus précisément, il s’agit d’une quartique unicursale. Une quartique est une courbe admettant une équation implicite de la forme ![]() où
où ![]() est de degré 4.
est de degré 4.
3 – Inverse d’une hyperbole équilatère
L’inversion de pole ![]() et de rapport
et de rapport ![]() est l’application du plan privé de
est l’application du plan privé de ![]() dans lui-même qui, à tout point d’affixe
dans lui-même qui, à tout point d’affixe ![]() fait correspondre celui d’affixe
fait correspondre celui d’affixe ![]()
Considérons l’hyperbole équilatère ![]() d’équation
d’équation ![]() c’est-à-dire :
c’est-à-dire : ![]()
Notons ![]() l’inversion de pôle l’origine et de rapport
l’inversion de pôle l’origine et de rapport ![]() Comme
Comme ![]() est involutive, un point
est involutive, un point ![]() d’affixe
d’affixe ![]() appartient à
appartient à ![]() si, et seulement si :
si, et seulement si :
![]()
![]()
L’image directe d’une hyperbole équilatère par l’inversion de pôle 0 est donc une lemniscate (privée de son centre). C’est ce que montre l’illustration dynamique ci-dessous.
Illustration dynamique
L’hyperbole et son inverse sont tracées respectivement en bleu et en orange.
Le pôle d’inversion est marqué par un petit disque vert.
Après avoir placé le curseur dans le cadre gris et en maintenant la touche SHIFT enfoncée, on peut déplacer le pôle à l’aide des flèches.
Une pression sur la touche Z ramène le pôle à l’origine : dans ce cas, l’inverse de l’hyperbole est une lemniscate.
4 – Podaire d’une hyperbole équilatère
La podaire d’une courbe ![]() par rapport à un point
par rapport à un point ![]() est le lieu des projections orthogonales de
est le lieu des projections orthogonales de ![]() sur les tangentes à
sur les tangentes à ![]()
Reprenons l’hyperbole ![]() introduite à la section précédente et déterminons, de deux manières, sa podaire par rapport à l’origine.
introduite à la section précédente et déterminons, de deux manières, sa podaire par rapport à l’origine.
– Premier calcul –
La branche d’hyperbole ![]() définie par les conditions
définie par les conditions ![]() et
et ![]() est paramétrée par :
est paramétrée par :
![Rendered by QuickLaTeX.com \[u\mapsto\left\{ \begin{array}{c}\cosh\left(u\right)\\\\\sinh\left(u\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-484bcad12f52de8fb9ab1be06e575803_l3.png)
![Rendered by QuickLaTeX.com \[t\mapsto Q_{t}\,:\,\left\{ \begin{array}{c}\cosh\left(u\right)+t\:\sinh\left(u\right)\\\\\sinh\left(u\right)+t\:\cosh\left(u\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f12de8b3913b79f34e8986e0b7506a28_l3.png)
![]()
![Rendered by QuickLaTeX.com \[u\mapsto Q_{t_{u}}\,:\,\left\{ \begin{array}{ccc}X & = & {\displaystyle \frac{\cosh\left(u\right)}{\cosh\left(2u\right)}}\\\\Y & = & {\displaystyle -\frac{\sinh\left(u\right)}{\cosh\left(2u\right)}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-08321b447fdb98e976b9587b4023ea6d_l3.png)
![]()
Comme ![]() reste positif, on reconnaît une ‘demi-lemniscate’. La lemniscate entière est obtenue en procédant de même avec
reste positif, on reconnaît une ‘demi-lemniscate’. La lemniscate entière est obtenue en procédant de même avec ![]()
– Second calcul, un peu plus simple –
Dans un repère dont les axes de coordonnées sont les asymptotes de l’hyperbole, celle-ci admet pour équation ![]()
La tangente ![]() en un point
en un point ![]() admet pour équation
admet pour équation ![]() c’est-à-dire :
c’est-à-dire : ![]()
Pour que le point ![]() soit le projeté orthogonal de
soit le projeté orthogonal de ![]() sur cette tangente, il faut que
sur cette tangente, il faut que ![]() et qu’en notant
et qu’en notant ![]() (vecteur qui dirige
(vecteur qui dirige ![]() on ait
on ait ![]() ce qui donne le système :
ce qui donne le système :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}bx+ay & = & 2\lambda^{2}\\\\-ax+by & = & 0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e6f56c82d9484564d801b662e46b8cf2_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}x & = & {\displaystyle \frac{2a}{a^{4}+1}}\\\\y & = & {\displaystyle \frac{2a^{3}}{a^{4}+1}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-11c252369eed2c1f65022fa8605ed58f_l3.png)
Illustration dynamique
L’hyperbole équilatère d’équation ![]() est tracée en bleu.
est tracée en bleu.
Sa podaire par rapport au point A représenté par un petit disque vert est tracée en orange.
A condition que le curseur soit dans la zone de visualisation, on peut :
- déplacer A avec les flèches (la touche SHIFT doit être maintenue enfoncée),
- ramener A à l’origine (touche Z), ce qui fait de la podaire une lemniscate,
- afficher / cacher la tangente au point courant de l’hyperbole (l’abscisse de ce point est celle du curseur) avec la touche T.
5 – Construction « mécanique » de la lemniscate
Deux cercles sont dits orthogonaux s’ils sont sécants et si, de plus, les tangentes en chacun de leurs deux points d’intersection sont perpendiculaires.
Soient ![]() et
et ![]() deux cercles orthogonaux de même rayon
deux cercles orthogonaux de même rayon ![]() Dans un repère convenable, leurs centres respectifs sont
Dans un repère convenable, leurs centres respectifs sont ![]() et
et ![]() La condition d’orthogonalité impose :
La condition d’orthogonalité impose : ![]() .
.
Etant donné ![]() , cherchons les points
, cherchons les points ![]() de
de ![]() vérifiant
vérifiant ![]()
Pour cela, introduisons les coordonnées de ![]() et de
et de ![]() :
:
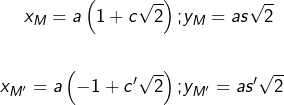
![]()
![]()
![]()
![]()
![]()
Cas 1 : ![]()
Cas 2 : 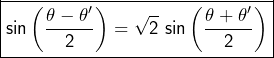 (■)
(■)
Le cas 1 est banal : la tige possède un mouvement de translation circulaire, qui évoque les locomotives à vapeur d’autrefois :
Le milieu de la tige décrit le cercle de centre ![]() et de rayon
et de rayon ![]() .
.
A présent, examinons le cas 2. Les coordonnées du milieu ![]() de
de ![]() sont :
sont :
![]()
![]()
(![]() )
) ![]()
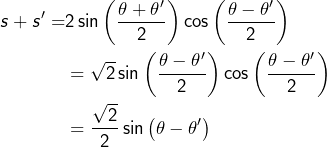
(![]() )
) ![]()
![]()
On reconnaît l’équation d’une lemniscate.
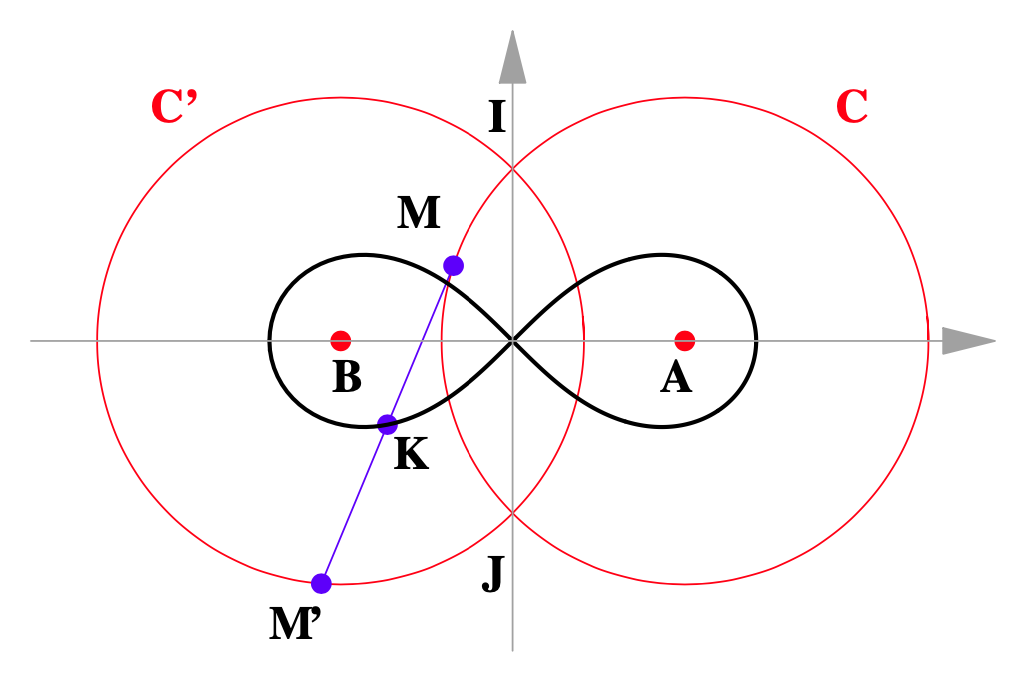
Encore faut-il vérifier que l’on obtient toute la lemniscate …
Il suffit pour cela de voir que, pour tout ![]() , l’équation (■) d’inconnue
, l’équation (■) d’inconnue ![]() ‘, possède une solution. Pour
‘, possède une solution. Pour ![]() , l’unique possibilité est
, l’unique possibilité est ![]() ; et pour
; et pour ![]() , on voit que :
, on voit que :
![Rendered by QuickLaTeX.com \[\boxed{\theta'=-2\arctan\left[\frac{\sqrt{2}-1}{\sqrt{2}+1}\tan\left(\frac{\theta}{2}\right)\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-96425a483ba995344db55ecce93e2e13_l3.png)
Illustration dynamique
Pour commencer, cliquer sur la zone de visualisation (pour la rendre active). A condition que le curseur s’y trouve, on peut :
- déplacer le stylet avec les touches SHIFT → et SHIFT ←
- sélectionner le mode (touche M) : translation circulaire ou lemniscate,
- (dés)activer le tracé automatique (touche A),
- effacer le tracé (touche Z).
6 – Projection centrale d’une fenêtre de Viviani
On appelle fenêtre de Viviani la courbe intersection d’une sphère de centre ![]() de rayon
de rayon ![]() et d’un cylindre de rayon
et d’un cylindre de rayon ![]() dont l’axe se situe à la distance
dont l’axe se situe à la distance ![]() de
de ![]() . Cette courbe
. Cette courbe ![]() est tracée sur la sphère (et sur le cylindre). Elle apparaît ci-dessous en rouge.
est tracée sur la sphère (et sur le cylindre). Elle apparaît ci-dessous en rouge.
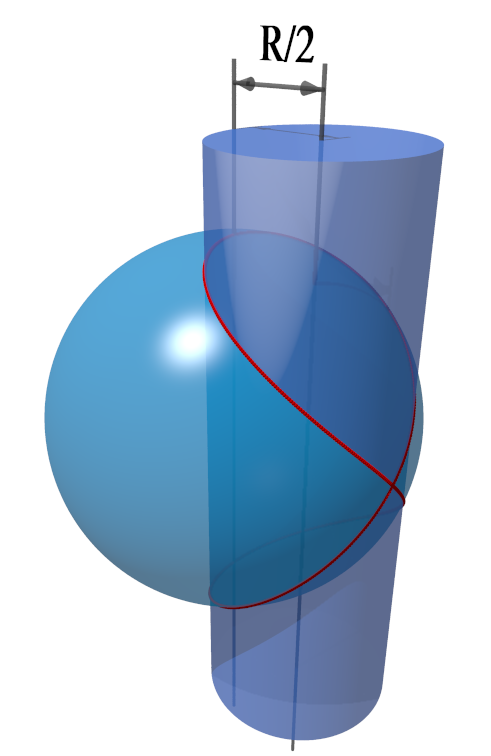
Par un choix convenable du système de coordonnées, on se ramène au cas de la sphère unité et du cylindre d’équation ![]()
Proposition
L’image directe de ![]() par la projection centrale de centre
par la projection centrale de centre ![]() sur le plan
sur le plan ![]() est une lemniscate.
est une lemniscate.
Une paramétrisation de ![]() est
est
![Rendered by QuickLaTeX.com \[u\mapsto M\left(u\right)\,:\,\left\{ \begin{array}{ccc}x & = & \sin\left(u\right)\,\cos\left(u\right)\\y & = & \cos^{2}\left(u\right)\\z & = & \sin\left(u\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ab08df03ce8d18121ddb0421fadce66_l3.png)
![Rendered by QuickLaTeX.com \[u\mapsto\left\{\begin{array}{ccc}X & = & {\displaystyle \frac{\sin\left(u\right)\,\cos\left(u\right)}{1+\cos^{2}\left(u\right)}}\\Y & = & 0\\Z & = & {\displaystyle \frac{\sin\left(u\right)}{1+\cos^{2}\left(u\right)}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6f265fc66b1ac680874bc81c834e3fd8_l3.png)
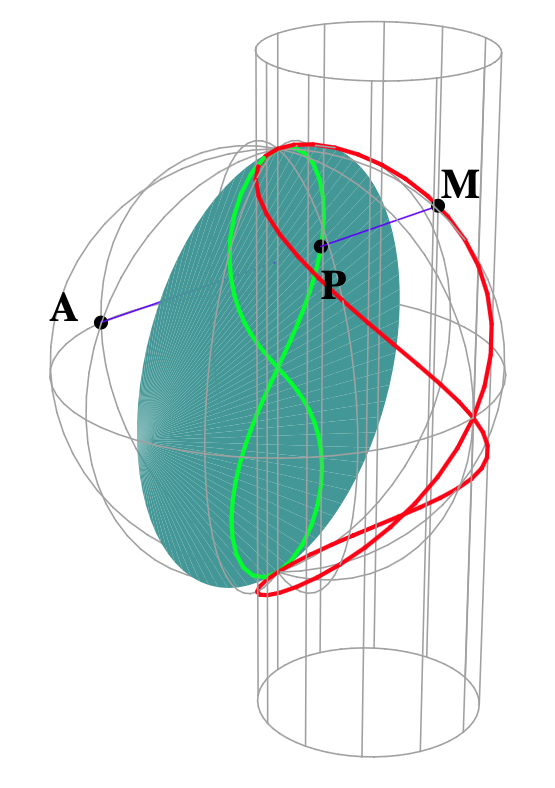
Remarque
En choisissant pour centre de projection le point ![]() qui est aussi le point double de
qui est aussi le point double de ![]() on obtient cette fois une hyperbole équilatère. On retrouve ainsi (cf. section 3) le fait que la lemniscate est l’inverse d’une hyperbole équilatère par rapport à son centre. Ceci découle du fait que les projections, à partir de deux points
on obtient cette fois une hyperbole équilatère. On retrouve ainsi (cf. section 3) le fait que la lemniscate est l’inverse d’une hyperbole équilatère par rapport à son centre. Ceci découle du fait que les projections, à partir de deux points ![]() diamétralement opposés d’une sphère de centre
diamétralement opposés d’une sphère de centre ![]() , sur le plan médiateur de
, sur le plan médiateur de ![]() donnent des figures transformées l’une de l’autre par l’inversion de pôle
donnent des figures transformées l’une de l’autre par l’inversion de pôle ![]() .
.
7 – Sections planes d’un tore
La rotation autour de l’axe ![]() du cercle d’équations
du cercle d’équations
![]()
![]()
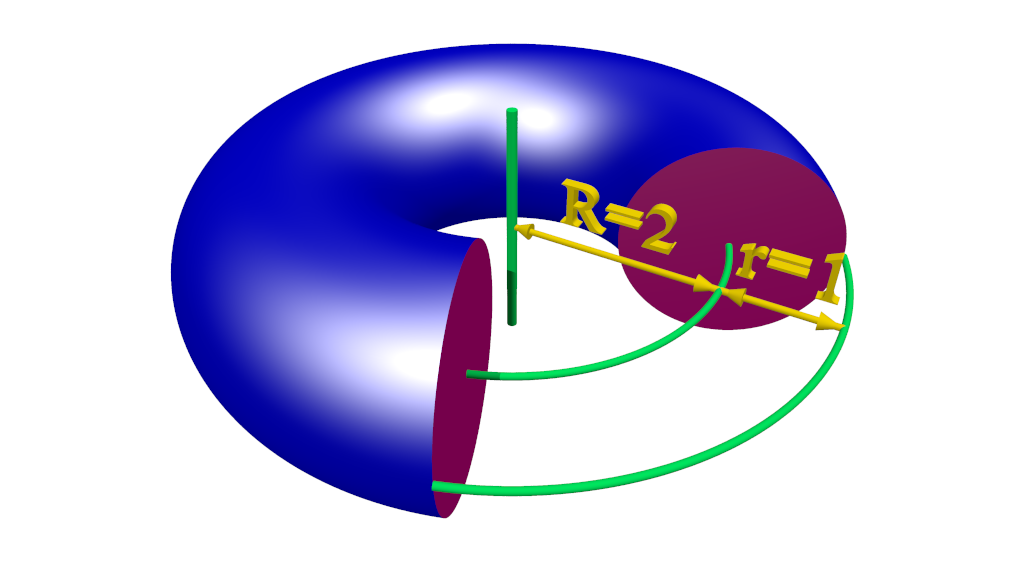
La section de ![]() par le plan d’équation
par le plan d’équation ![]() est une courbe en forme de huit, comme le suggère la figure ci-dessous :
est une courbe en forme de huit, comme le suggère la figure ci-dessous :
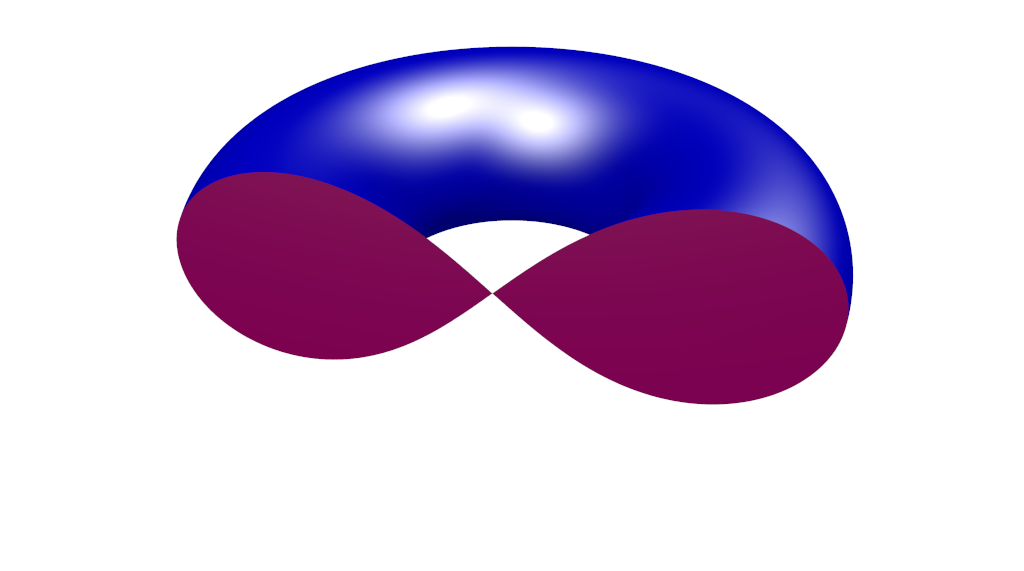
Pour ![]() cette intersection admet pour équations :
cette intersection admet pour équations :
![]()
![]()
Les différentes sections de ![]() par des plans verticaux (dont celle donnant une lemniscate) sont visibles dans l’animation ci-dessous. Le rayon principal de
par des plans verticaux (dont celle donnant une lemniscate) sont visibles dans l’animation ci-dessous. Le rayon principal de ![]() est
est ![]() son rayon secondaire (celui du cercle générateur) est
son rayon secondaire (celui du cercle générateur) est ![]() La distance de l’origine au plan sécant est
La distance de l’origine au plan sécant est ![]() donc
donc ![]() sur cet exemple (la lemniscate étant obtenue pour
sur cet exemple (la lemniscate étant obtenue pour ![]() :
:
8 – Enveloppe d’une famille de cercles
On peut montrer que l’enveloppe de la famille des cercles centrés sur une hyperbole équilatère et qui passent par son centre est une lemniscate.
En effet, considérons la famille ![]() des cercles centrés sur la branche droite de l’hyperbole équilatère
des cercles centrés sur la branche droite de l’hyperbole équilatère ![]() d’équation
d’équation ![]() :
:
(![]() )
) ![]()
(![]() )
) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Illustration dynamique
On voit ci-dessous une hyperbole équilatère H (tracée en bleu) ainsi qu’une partie de la famille des cercles centrés sur H et qui passent par son centre.
Le slider permet de faire varier le nombre de cercles.
L’enveloppe de cette famille de cercles est une lemniscate. On la devine aisément (bien qu’elle ne soit pas explicitement dessinée) si le nombre de cercles est suffisant.
Remarque
Comme expliqué sur cette page du site https://mathcurve.com/, les constructions par enveloppe d’une famille de cercles ou par podaire (cf. section 4) sont équivalentes, pour une courbe très générale : la podaire d’une courbe ![]() par rapport à un point O est l’enveloppe des cercles de diamètre
par rapport à un point O est l’enveloppe des cercles de diamètre ![]() , où le point M décrit
, où le point M décrit ![]() .
.
9 – Epilogue
Comme signalé plus haut, la courbe d’équation polaire ![]() est une lemniscate. L’aire d’un lobe est donnée par :
est une lemniscate. L’aire d’un lobe est donnée par :
![Rendered by QuickLaTeX.com \[\frac{1}{2}\,\int\,r^{2}\,d\theta=\frac{a^{2}}{2}\,\int_{-\pi/4}^{\pi/4}\,\cos\left(2\theta\right)\,d\theta=\frac{a^{2}}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a2c16c7fcbbe97a460baeb499f60e51_l3.png)
![]()
Quant au calcul de la longueur d’une lemniscate, c’est une autre paire de manche ! Cette question est étroitement liée à la théorie des fonctions elliptiques.
Seules quelques propriétés de la lemniscate ont été évoquées dans cet article. On pourra en découvrir d’autres en consultant l’excellent site MathCurve de Robert Ferréol.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.



Au tout debut, n’est ce pas toujours k^4 pour le second membre de chaque equation. Peut etre un typo.
Merci
– Joseph
Oui, absolument ! Je rectifie … Merci Joseph de me l’avoir signalé 🙂