Lettre R
RACINE CARRÉE
Etant donné un nombre réel ![]() , on peut montrer que l’équation
, on peut montrer que l’équation ![]() d’inconnue
d’inconnue ![]() possède deux solutions opposées (confondues si
possède deux solutions opposées (confondues si ![]() ).
).
Celle qui est positive est la racine carrée de ![]() ; on la note
; on la note ![]() ou
ou ![]() .
.
Si ![]() , il n’existe aucune solution réelle à l’équation
, il n’existe aucune solution réelle à l’équation ![]() .
.
Par exemple :
![]()
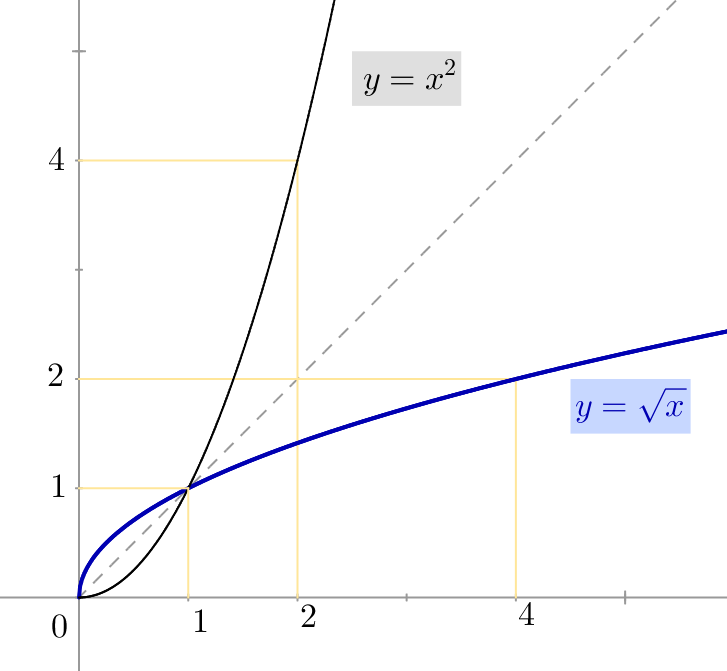
L’application ![]() est la bijection réciproque de
est la bijection réciproque de ![]() .
.
Proposition
Pour tout ![]() :
:
![]()
Exemple
![]()
On peut montrer que si ![]() n’est pas le carré d’un entier, alors
n’est pas le carré d’un entier, alors ![]() .
.
Dans le corps ![]() , tout
, tout ![]() possède deux racines carrées opposées et l’usage du symbole
possède deux racines carrées opposées et l’usage du symbole ![]() est proscrit (ou, tout au moins, pas recommandé à un niveau élémentaire, en raison de son ambiguïté : en l’absence de relation d’ordre dans
est proscrit (ou, tout au moins, pas recommandé à un niveau élémentaire, en raison de son ambiguïté : en l’absence de relation d’ordre dans ![]() , on ne peut pas distinguer de solution « positive » parmi les deux solutions complexes de l’équation
, on ne peut pas distinguer de solution « positive » parmi les deux solutions complexes de l’équation ![]() … ).
… ).
D’une manière générale, si ![]() est un anneau et si
est un anneau et si ![]() , les racines carrées dans
, les racines carrées dans ![]() de
de ![]() sont les (éventuelles) solutions de l’équation
sont les (éventuelles) solutions de l’équation ![]() , d’inconnue
, d’inconnue ![]() .
.
Dans l’anneau ![]() des matrices carrées réelles de taille
des matrices carrées réelles de taille ![]() , certains éléments ne possèdent aucune racine carrée, d’autres en possède un nombre fini, d’autres encore en possèdent une infinité.
, certains éléments ne possèdent aucune racine carrée, d’autres en possède un nombre fini, d’autres encore en possèdent une infinité.
Dans le corps ![]() (pour
(pour ![]() premier impair), il existe
premier impair), il existe ![]() éléments possédant une racine carrée et
éléments possédant une racine carrée et ![]() éléments n’en possédant pas.
éléments n’en possédant pas.
RÉCIPROQUE (bijection)
Théorème et définition
Soient ![]() deux ensembles non vides.
deux ensembles non vides.
Si ![]() est une bijection, on note
est une bijection, on note ![]() l’application de
l’application de ![]() vers
vers ![]() qui, à chaque élément de
qui, à chaque élément de ![]() , associe son unique antécédent par
, associe son unique antécédent par ![]()
![]() est une bijection, appelée bijection réciproque (ou simplement : réciproque) de
est une bijection, appelée bijection réciproque (ou simplement : réciproque) de ![]()
C’est l’unique application ![]() vérifiant
vérifiant ![]() et
et ![]()
Exemple 1
L’application
![]()
![]()
Exemple 2
L’application
![]()
![]()
Exemple 3
L’application
![]()
Revenons un instants aux généralités.
Proposition : réciproque d’une composée
Si ![]() sont trois ensembles non vides et si
sont trois ensembles non vides et si ![]() et
et ![]() sont des bijections, alors
sont des bijections, alors ![]() est une bijection et :
est une bijection et :
![]()
Signalons un point de vue géométrique.
Proposition : graphe d’une réciproque
Etant données deux parties ![]() de
de ![]() et une bijection
et une bijection ![]() chacun des graphes de
chacun des graphes de ![]() et de
et de ![]() est l’image directe de l’autre par la réflexion d’axe
est l’image directe de l’autre par la réflexion d’axe ![]() où
où ![]() désigne la première bissectrice (la droite de
désigne la première bissectrice (la droite de ![]() d’équation
d’équation ![]()
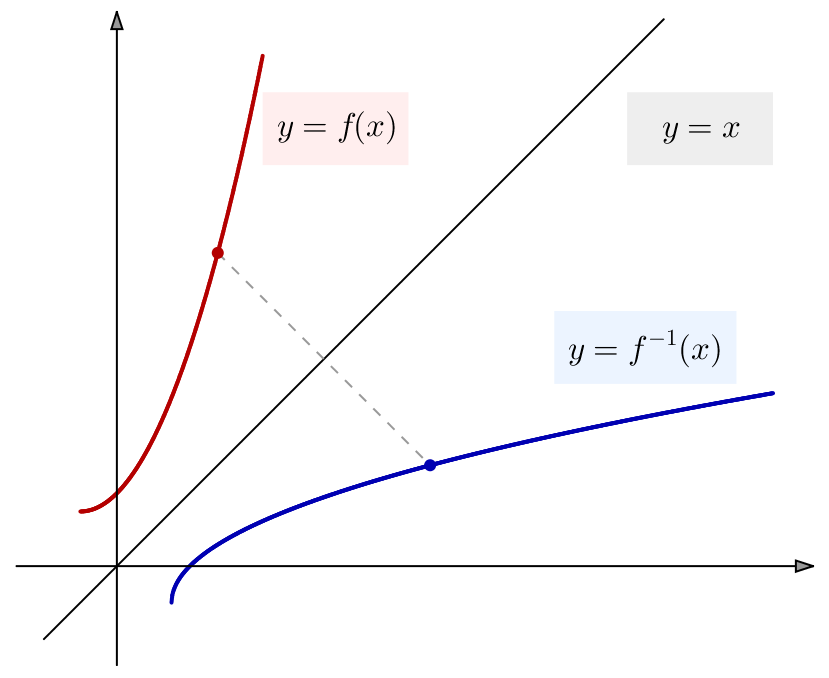
C’est ainsi que les graphes de ![]() et de
et de ![]() sont symétriques par rapport à
sont symétriques par rapport à ![]() Même chose pour les graphes de
Même chose pour les graphes de ![]() et de
et de ![]()
Exemple 4
Si ![]() est un ensemble et si
est un ensemble et si ![]() notons
notons ![]() le complémentaire de
le complémentaire de ![]() dans
dans ![]() L’application
L’application
![]()
Il s’agit d’un cas particulier d’involution. Les involutions d’un ensemble non vide ![]() sont les applications
sont les applications ![]() vérifiant
vérifiant ![]()
Certaines fonctions usuelles sont définies comme des bijections réciproques. C’est notamment le cas de arcsin, arccos, arctan ou encore argsh, argch, argth. Un autre exemple célèbre est celui des fonctions elliptiques de Jacobi :
Exemple 5
![]() étant fixé, l’application
étant fixé, l’application
![Rendered by QuickLaTeX.com \[F_{k}:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\int_{0}^{x}\frac{1}{\sqrt{1-k^{2}\sin^{2}\left(t\right)}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8563e92462ca06bc6b863e2ecc849d9f_l3.png)
Jacobi
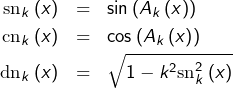
Terminons avec quelques propriétés importantes d’une bijection réciproque (sans aucune prétention d’exhaustivité) :
Propriétés d’une réciproque
Soient ![]() deux intervalles non triviaux et soit
deux intervalles non triviaux et soit ![]() une bijection.
une bijection.
- Si
 est strictement monotone, alors
est strictement monotone, alors  aussi et les sens de variation sont les mêmes.
aussi et les sens de variation sont les mêmes. - Si
 est impaire, alors
est impaire, alors 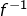 aussi (les intervalles I et J sont en outre supposés symétriques par rapport à 0).
aussi (les intervalles I et J sont en outre supposés symétriques par rapport à 0). - Si
 est continue, alors
est continue, alors 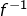 aussi.
aussi. - Si
 est dérivable et si
est dérivable et si 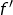 ne s’annule pas, alors
ne s’annule pas, alors 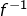 est dérivable et :
est dérivable et :![Rendered by QuickLaTeX.com \[\left(f^{-1}\right)'=\frac{1}{f'\circ f^{-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a15e7fb6c8e2b107a2d3b0bffc7d40e_l3.png)
- Si
 est de classe
est de classe 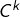 (avec
(avec  et si
et si 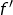 ne s’annule pas, alors
ne s’annule pas, alors 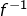 est aussi de classe
est aussi de classe 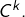
RÉEL (nombre)
De façon naïve, les nombres réels sont tous les nombres que l’on peut associer à un point d’une droite ![]() après avoir choisi un repère normé pour celle-ci. En clair : on commence par choisir deux points de
après avoir choisi un repère normé pour celle-ci. En clair : on commence par choisir deux points de ![]() l’un est associé à 0 et l’autre à 1. Après cela, une correspondance bijective est établie entre
l’un est associé à 0 et l’autre à 1. Après cela, une correspondance bijective est établie entre ![]() et
et ![]() : chaque point est associé à un nombre réel bien déterminé et réciproquement. L’illustration ci-dessous donne une idée de cette correspondance :
: chaque point est associé à un nombre réel bien déterminé et réciproquement. L’illustration ci-dessous donne une idée de cette correspondance :
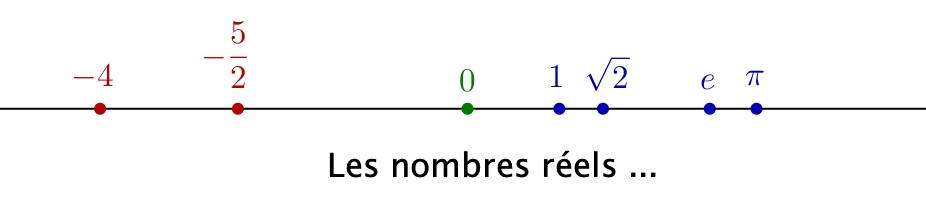
On peut aussi se représenter un nombre réel par son développement décimal illimité :

Mais il faut bien reconnaître que cette écriture, avec ses points de suspension, manque cruellement de rigueur. Pour une construction sérieuse de
Brève énumération de quelques sous-ensembles importants de ![]() :
:
- l’ensemble
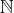 des entiers naturels : 0, 1, 2, 3, etc …
des entiers naturels : 0, 1, 2, 3, etc … - l’ensemble
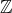 des entiers relatifs : …, -3, -2, -1, 0, 1, 2, 3, …
des entiers relatifs : …, -3, -2, -1, 0, 1, 2, 3, … - l’ensemble
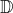 des nombres décimaux : ce sont les
des nombres décimaux : ce sont les 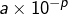 pour
pour  et
et 
- l’ensemble
 des nombres rationnels, c’est-à-dire de la forme
des nombres rationnels, c’est-à-dire de la forme 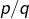 avec
avec 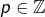 et
et 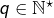
- l’ensemble
 des nombres irrationnels : tous les réels … qui ne sont pas rationnels !
des nombres irrationnels : tous les réels … qui ne sont pas rationnels ! 
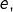
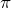 et beaucoup, beaucoup d’autres …
et beaucoup, beaucoup d’autres … - l’ensemble
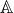 des nombres algébriques : ce sont les solutions d’équations de la forme
des nombres algébriques : ce sont les solutions d’équations de la forme 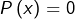 avec
avec 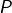 un polynôme de degré
un polynôme de degré 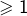 à coefficients entiers.
à coefficients entiers.
Ces ensembles, à l’exception de ![]() sont dotés d’une structure algébrique (
sont dotés d’une structure algébrique (![]() et
et ![]() sont des anneaux,
sont des anneaux, ![]() et
et ![]() sont des corps).
sont des corps).
Schéma d’une construction du corps des nombres réels
En supposant connu le corps ![]() des rationnels, on peut construire un corps totalement ordonné, archimédien et complet admettant un sous-corps isomorphe à
des rationnels, on peut construire un corps totalement ordonné, archimédien et complet admettant un sous-corps isomorphe à ![]() En outre, un tel corps est unique à isomorphisme (de corps) près.
En outre, un tel corps est unique à isomorphisme (de corps) près.
Voici, dans les grandes lignes, le plan d’une telle construction : on quotiente l’anneau des suites de Cauchy de rationnels par l’idéal constitué des suites de limite nulle. Comme cet idéal est maximal, le quotient est un corps, que l’on note ![]() En associant à tout rationnel la classe de la suite constante qu’il définit, on établit un morphisme injectif de corps, qui permet d’identifier
En associant à tout rationnel la classe de la suite constante qu’il définit, on établit un morphisme injectif de corps, qui permet d’identifier ![]() à un sous-corps de
à un sous-corps de ![]() Il reste à prouver le caractère archimédien et la complétude de
Il reste à prouver le caractère archimédien et la complétude de ![]()
Cette construction, attribuée à Charles Meray ainsi qu’à Georg Cantor n’est qu’une parmi d’autres. Le mathématicien allemand Richard Dedekind en a proposé une autre, reposant sur la notion de coupures de rationnels.
RIEMANN (série de)
Les séries de la forme  (pour
(pour ![]() sont appelées séries de Riemann.
sont appelées séries de Riemann.

On montre qu’une telle série converge si, et seulement si, ![]() Sa somme est la fonction zeta de Riemann :
Sa somme est la fonction zeta de Riemann :
![Rendered by QuickLaTeX.com \[\boxed{\zeta\left(z\right)=\sum_{n=1}^{\infty}\frac{1}{n^{z}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e6370e21e2df3f83c58c905bec4a9053_l3.png)
Pour ![]() il s’agit de la célèbre série harmonique.
il s’agit de la célèbre série harmonique.
Euler a découvert la formule explicite suivante :
![]()
![]()
![]()
Euler a aussi découvert l’identité fondamentale suivante :
![Rendered by QuickLaTeX.com \[\forall s>1,\,\zeta\left(s\right)=\prod_{p\in\mathbb{P}}\left(1-\frac{1}{p^{s}}\right)^{-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4bc24c26dba0025bd93de9620121dea5_l3.png)
Mais c’est à Riemann que l’on doit d’avoir eu l’idée d’étudier la fonction ![]() dans le champ complexe. Il a prouvé que
dans le champ complexe. Il a prouvé que ![]() se prolonge en une fonction holomorphe sur
se prolonge en une fonction holomorphe sur ![]() Ce nouveau cadre a permis, dès la fin du XIXème siècle, à Hadamard et de la Vallée Poussin de démontrer (indépendamment) le théorème des nombres premiers, selon lequel le nombre, noté
Ce nouveau cadre a permis, dès la fin du XIXème siècle, à Hadamard et de la Vallée Poussin de démontrer (indépendamment) le théorème des nombres premiers, selon lequel le nombre, noté ![]() , de nombres premiers inférieurs à
, de nombres premiers inférieurs à ![]() croît comme
croît comme ![]() .
.
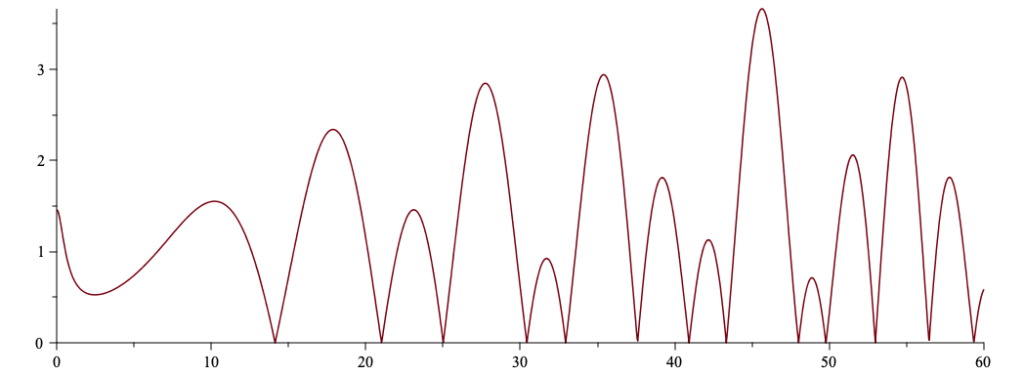
Riemann a aussi formulé une célèbre hypothèse (non démontrée à ce jour) et qui porte son nom. Cette hypothèse affirme que les seuls zéros non triviaux (c’est-à-dire ceux qui ne sont pas des entiers pairs strictement négatifs) du prolongement de ![]() sont situés sur la droite d’équation
sont situés sur la droite d’équation ![]() L’illustration ci-dessous montre une portion du graphe de :
L’illustration ci-dessous montre une portion du graphe de :
![]()
ROLLE (Lemme de)
Lemme de ROLLE
Soient ![]() deux réels tels que
deux réels tels que ![]() et soit
et soit ![]() continue. Si de plus
continue. Si de plus ![]() est dérivable sur
est dérivable sur ![]() et si
et si ![]() alors :
alors :
![]()
Si ![]() est constante, le résultat est évident. Et sinon, on observe que
est constante, le résultat est évident. Et sinon, on observe que ![]() atteint l’une au moins de ses deux bornes en un point
atteint l’une au moins de ses deux bornes en un point ![]() intérieur au segment
intérieur au segment ![]() Si par exemple
Si par exemple ![]() alors le taux d’accroissement :
alors le taux d’accroissement :
![]()
- positif ou nul lorsque
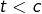
- négatif ou nul lorsque

ce qui entraîne ![]() La situation est analogue si
La situation est analogue si ![]()
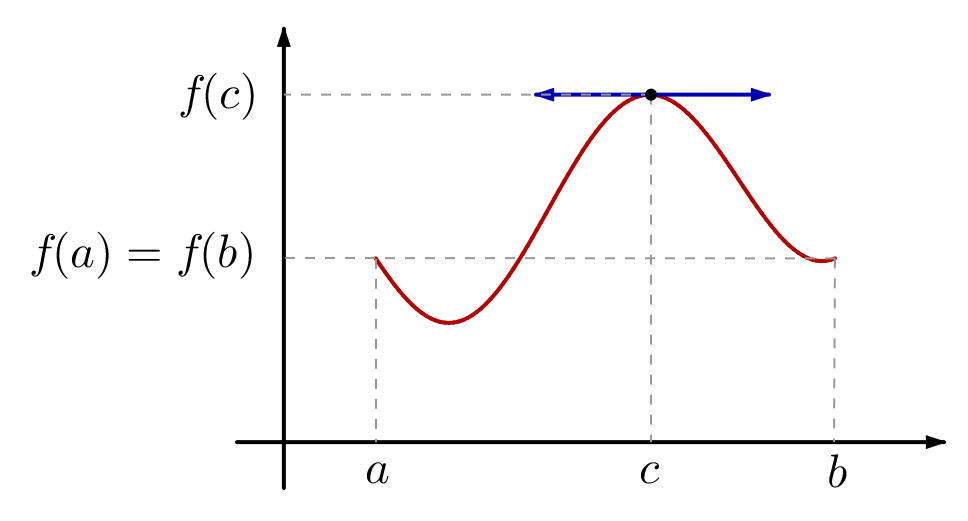
Le lemme de Rolle admet, parmi ses corollaires, la célèbre …
Formule des accroissements finis
Soient ![]() deux réels tels que
deux réels tels que ![]() et soit
et soit ![]() continue. Si de plus
continue. Si de plus ![]() est dérivable sur
est dérivable sur ![]() alors :
alors :
![]()
Il suffit d’appliquer le lemme de Rolle à :
![]()
Cette formule s’interprète géométriquement : il existe un point du graphe de ![]() en lequel la tangente est parallèle à la droite joignant les points du graphe d’abscisses
en lequel la tangente est parallèle à la droite joignant les points du graphe d’abscisses ![]() et
et ![]() .
.
Parmi les principales applications de cette formule, on peut citer :
Proposition
Soit ![]() un intervalle non trivial et soit
un intervalle non trivial et soit ![]() une application dérivable. Si
une application dérivable. Si
![]()
Cette implication est à la base de la méthode usuelle d’étude des variations des fonctions numériques. Signalons que sa réciproque est vraie (mais moins intéressante).

