
L’algèbre linéaire consiste, grosso modo, en l’étude des propriétés des espaces vectoriels et des applications linéaires. Et lorsqu’on examine une application linéaire, on commence souvent par en chercher le noyau et / ou l’image.
C’est précisément ce point qui fait l’objet du présent article.
Après avoir rappelé les indispensables définitions, je détaillerai pour vous quelques exemples de difficulté graduée et je présenterai aussi quelques considérations théoriques, indispensables pour comprendre l’utilité de ces notions.
1 – Bref rappel sur les applications linéaires
Afin de respecter le contour des programmes de mathématiques des deux premières années d’enseignement supérieur scientifique, le cadre retenu sera celui des espaces vectoriels sur un corps ![]() (ce contexte pourrait être élargi à celui des modules sur un anneau commutatif).
(ce contexte pourrait être élargi à celui des modules sur un anneau commutatif).
Etant donnés deux espaces vectoriels ![]() et
et ![]() sur un même corps
sur un même corps ![]() une application
une application ![]() est dite linéaire lorsqu’elle « préserve la structure vectorielle », au sens suivant :
est dite linéaire lorsqu’elle « préserve la structure vectorielle », au sens suivant :
- l’image de la somme de deux vecteurs est égale à la somme des images,
- l’image du produit d’un scalaire
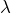 par un vecteur est égale au produit de
par un vecteur est égale au produit de 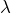 par l’image du vecteur.
par l’image du vecteur.
En d’autres termes, une application linéaire est un « morphisme d’espaces vectoriels ».
Voici la version formalisée de la double-condition précédente :
Tout ceci équivaut à l’unique condition suivante :
![]()
Deux corollaires immédiats :
Corollaire 1
Par une application linéaire de ![]() vers
vers ![]() :
:
l’image du vecteur nul de ![]() est le vecteur nul de
est le vecteur nul de ![]() .
.
En effet, en notant ![]() et
et ![]() les vecteurs nuls respectifs de
les vecteurs nuls respectifs de ![]() et
et ![]() :
:
![]()
Corollaire 2
Par une application linéaire :
l’image de toute combinaison linéaire est la combinaison linéaire
correspondante (ie : avec les mêmes coefficients) des images.
En symboles :
![]()
![Rendered by QuickLaTeX.com \[u\left(\sum_{i=1}^{n}\lambda_{i}x_{i}\right)=\sum_{i=1}^{n}\lambda_{i}\thinspace u\left(x_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-24f086b251f58d0fdf29eddd48c421ab_l3.png)
Ceci se démontre aisément, par récurrence sur le nombre de termes.
En parcourant la deuxième section de l’article Comment définir une application linéaire ? vous trouverez quelques exemples variés d’applications linéaires.
Ajoutons que l’ensemble ![]() des applications linéaires de
des applications linéaires de ![]() vers
vers ![]() est naturellement muni d’une structure d’espace vectoriel, puisqu’il s’agit d’un sev de l’espace de toutes les applications de
est naturellement muni d’une structure d’espace vectoriel, puisqu’il s’agit d’un sev de l’espace de toutes les applications de ![]() vers
vers ![]() (linéaires ou non).
(linéaires ou non).
Lorsque ![]() , la notation
, la notation ![]() se simplifie en
se simplifie en ![]() Les applications linéaires de
Les applications linéaires de ![]() dans lui-même sont appelées les endomorphismes de
dans lui-même sont appelées les endomorphismes de ![]()
Quant aux applications linéaires de ![]() dans
dans ![]() elle sont appelées formes linéaires sur
elle sont appelées formes linéaires sur ![]()
2 – Noyau et image : qu’est-ce donc ?
Définitions
Si ![]() alors :
alors :
➡ l’image de ![]() est l’ensemble des vecteurs de
est l’ensemble des vecteurs de ![]() qui sont atteints par
qui sont atteints par ![]()
➡ le noyau de ![]() est l’ensemble des vecteurs de
est l’ensemble des vecteurs de ![]() dont l’image par
dont l’image par ![]() est nulle.
est nulle.
L’image et le noyau de ![]() sont notés
sont notés ![]() et
et ![]() Ce sont des sev de
Ce sont des sev de ![]() et de
et de ![]() respectivement.
respectivement.
Plus généralement, si ![]() un sous-espace vectoriel de
un sous-espace vectoriel de ![]() et si
et si ![]() un sous-espace vectoriel de
un sous-espace vectoriel de ![]() alors :
alors :
- l’image directe de
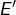 par
par  est un sous-espace vectoriel de
est un sous-espace vectoriel de 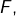
- l’image réciproque de
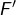 par
par  est un sous-espace vectoriel de
est un sous-espace vectoriel de 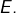
Une preuve détaillée de la seconde partie de cette affirmation est donnée dans l’article :
Image directe / image réciproque d’une partie
L’image et le noyau de ![]() apparaissent alors comme des cas particuliers :
apparaissent alors comme des cas particuliers :
- en prenant
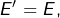 on trouve
on trouve 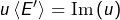
- en prenant
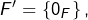 on trouve
on trouve 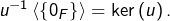
3 – Quelques exemples explicites
Exemple 1
L’application :
![]()
![]()
Au début de la section 4, on verra ce qu’on peut dire – de manière générale – concernant l’image d’une forme linéaire.
Exemple 2
L’application :
![]()
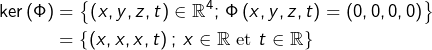
On reconnaît le plan
En particulier
![]()
![]()
![]()
Question
Sauriez-vous déterminer le noyau et l’image de l’application linéaire
![]()
Exemple 3
On note classiquement ![]() l’endomorphisme de
l’endomorphisme de ![]() défini par :
défini par :
![]()
Par exemple, si ![]() est le polynôme
est le polynôme ![]() alors :
alors :
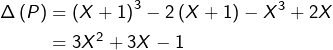
Le noyau de ![]() est constitué des polynômes
est constitué des polynômes ![]() vérifiant
vérifiant ![]()
Si un tel polynôme possède une racine réelle ![]() alors :
alors :
![]()
Par récurrence, on constate que ![]() pour tout
pour tout ![]() De ce fait,
De ce fait, ![]() possède une infinité de racines : c’est le polynôme nul.
possède une infinité de racines : c’est le polynôme nul.
Et si ![]() n’a pas de racines réelles, qu’à cela ne tienne: on considère
n’a pas de racines réelles, qu’à cela ne tienne: on considère ![]() avec
avec ![]() quelconque. De toute évidence :
quelconque. De toute évidence : ![]()
On peut donc appliquer ce qui précède à ![]() et conclure que
et conclure que ![]() En définitive, si
En définitive, si ![]() alors
alors ![]() est constant.
est constant.
Réciproquement, il est évident que les polynômes constants appartiennent à ![]()
En conclusion : ![]() est l’espace des polynômes constants (qui est une droite vectorielle). En particulier,
est l’espace des polynômes constants (qui est une droite vectorielle). En particulier, ![]() n’est pas injectif puisque
n’est pas injectif puisque ![]() .
.
Question
Sauriez-vous déterminer l’image de ![]() ? Solution en annexe.
? Solution en annexe.
Exemple 4
Revenons aux formes linéaires, pour dire un mot de la trace d’une matrice carrée.
A toute matrice carrée ![]() de taille
de taille ![]() et à termes dans
et à termes dans ![]() on associe la somme de ses termes diagonaux, appelée trace de
on associe la somme de ses termes diagonaux, appelée trace de ![]() et notée
et notée ![]()
![Rendered by QuickLaTeX.com \[\text{Si}\quad A=\left[\begin{array}{ccccc}a_{1,1} & a_{1,2} & \cdots & \cdots & a_{1,n}\\a_{2,1} & a_{2,2} & \ddots & & \vdots\\\vdots & \ddots & \ddots & \ddots & \vdots\\\vdots & & \ddots & \ddots & a_{n-1,n}\\a_{n,1} & \cdots & \cdots & a_{n,n-1} & a_{n,n}\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d236944f4d49a8d22fe6fd822e2e1ccb_l3.png)
![Rendered by QuickLaTeX.com \[\text{alors tr}\left(A\right)=\sum_{i=1}^{n}a_{i,i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2e555b83fd33b17123f734d5c3a09609_l3.png)
On peut démontrer la :
Proposition
Si le corps ![]() est de caractéristique nulle, alors le noyau de
est de caractéristique nulle, alors le noyau de ![]() (qui est, par définition, l’ensemble des matrices de trace nulle) est constitué des matrices semblables à une matrice de diagonale nulle.
(qui est, par définition, l’ensemble des matrices de trace nulle) est constitué des matrices semblables à une matrice de diagonale nulle.

ATTENTION … en caractéristique ![]() (avec
(avec ![]() premier), on n’a plus qu’une inclusion. En effet, une matrice de la forme
premier), on n’a plus qu’une inclusion. En effet, une matrice de la forme ![]() avec
avec ![]() de trace nulle sera de trace nulle, mais la matrice unité de taille
de trace nulle sera de trace nulle, mais la matrice unité de taille ![]() à termes dans le corps
à termes dans le corps ![]() est de trace nulle sans être semblable à une matrice de diagonale nulle.
est de trace nulle sans être semblable à une matrice de diagonale nulle.
Démontrons la proposition ci-dessus en nous limitant à des matrices de taille 2 (le cas général se traiterait par récurrence sur la taille de la matrice).
Preuve (cliquer pour déplier / replier)
Soit ![]() telle que
telle que ![]()
Notons ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() Cela signifie que
Cela signifie que ![]() et que
et que ![]() est la matrice de
est la matrice de ![]() relativement à la base canonique de
relativement à la base canonique de ![]() .
.
Si ![]() est une homothétie, disons
est une homothétie, disons ![]() alors
alors ![]() et donc
et donc ![]() (puisque
(puisque ![]() n’est pas de caractéristique 2). La matrice
n’est pas de caractéristique 2). La matrice ![]() est nulle dans ce cas.
est nulle dans ce cas.
Et sinon, on sait qu’il existe ![]() tel que la famille
tel que la famille ![]() soit libre (ceci résulte d’une caractérisation classique : un endomorphisme
soit libre (ceci résulte d’une caractérisation classique : un endomorphisme ![]() est une homothétie si, et seulement si, pour tout vecteur
est une homothétie si, et seulement si, pour tout vecteur ![]() la famille
la famille ![]() est liée). Cette famille est donc une base de
est liée). Cette famille est donc une base de ![]() dans laquelle
dans laquelle ![]() est représenté par une matrice de la forme :
est représenté par une matrice de la forme :
![]()
Question
Juste après la proposition précédente et dans la preuve de celle-ci, on a implicitement utilisé le fait que deux matrices semblables (en l’occurrence ![]() et
et ![]() ont la même trace.
ont la même trace.
Sauriez-vous prouver ceci en toute généralité ?
Réponse en annexe.
Exemple 5
On note ![]() l’espace vectoriel des applications continues de
l’espace vectoriel des applications continues de ![]() dans
dans ![]() et
et ![]() celui des applications de classe
celui des applications de classe ![]() (c’est-à-dire : dérivables et à dérivée continue). On considère alors l’application :
(c’est-à-dire : dérivables et à dérivée continue). On considère alors l’application :
![]()

En choisissant pour ensemble de départ l’espace ![]() des applications dérivables de
des applications dérivables de ![]() dans
dans ![]() et, comme ensemble d’arrivée, l’espace
et, comme ensemble d’arrivée, l’espace ![]() de toutes les applications de
de toutes les applications de ![]() dans
dans ![]() la dérivation serait toujours linéaire, son noyau serait toujours le même (la droite vectorielle constituée des applications constantes) mais elle ne serait pas surjective ! Il existe en effet des applications de
la dérivation serait toujours linéaire, son noyau serait toujours le même (la droite vectorielle constituée des applications constantes) mais elle ne serait pas surjective ! Il existe en effet des applications de ![]() dans
dans ![]() ne possédant pas de primitives (d’ailleurs, d’après un célèbre théorème de Darboux, une application de
ne possédant pas de primitives (d’ailleurs, d’après un célèbre théorème de Darboux, une application de ![]() dans
dans ![]() doit nécessairement vérifier la propriété des valeurs intermédiaires pour posséder une primitive).
doit nécessairement vérifier la propriété des valeurs intermédiaires pour posséder une primitive).
Question
![]() désigne un intervalle non trivial de
désigne un intervalle non trivial de ![]() . Sauriez-vous trouver un exemple d’application
. Sauriez-vous trouver un exemple d’application ![]() ne possédant aucune primitive ?
ne possédant aucune primitive ?
Solution en annexe.
4 – Injectivité et noyau
Rappelons qu’une application ![]() est dite injective lorsque deux éléments distincts de
est dite injective lorsque deux éléments distincts de ![]() ont nécessairement des images distinctes par
ont nécessairement des images distinctes par ![]() Formulation équivalente et plus maniable :
Formulation équivalente et plus maniable :
![]()
Voir à ce sujet la vidéo : Correspondances, Fonctions, Applications (1)
Dans le cas d’une application linéaire, il est commode de caractériser l’injectivité par le noyau :
Proposition
Soient ![]() deux espaces vectoriels et soit
deux espaces vectoriels et soit ![]() Alors :
Alors :
![]()
Preuve (cliquer pour déplier / replier)
Supposons d’abord ![]() injective.
injective.
Comme ![]() est linéaire, on sait que
est linéaire, on sait que ![]() ce qui dit exactement que
ce qui dit exactement que ![]()
En outre, si ![]() alors
alors ![]() et donc
et donc ![]() par injectivité.
par injectivité.
Ceci montre que ![]() . On a prouvé par double inclusion que :
. On a prouvé par double inclusion que :
![]()
Réciproquement, supposons que ![]() et donnons-nous deux vecteurs
et donnons-nous deux vecteurs ![]() tels que
tels que ![]()
Cette égalité peut s’écrire ![]() elle exprime donc le fait que
elle exprime donc le fait que ![]() Ainsi
Ainsi ![]() et l’injectivité de
et l’injectivité de ![]() est établie.
est établie.
Donnons deux exemples.
Exemple 1
Notons ![]() l’espace des applications de classe
l’espace des applications de classe ![]() de
de ![]() dans
dans ![]() qui s’annulent en
qui s’annulent en ![]()
L’application
![]()
Exemple 2
Soit ![]() un
un ![]() -espace vectoriel et soient
-espace vectoriel et soient ![]() deux sev de
deux sev de ![]() Alors l’application :
Alors l’application :
![]()
En effet, supposons que ![]() et soit
et soit ![]() Alors
Alors ![]() c’est-à-dire
c’est-à-dire ![]() Comme
Comme ![]() est stable par combinaison linéaire, alors
est stable par combinaison linéaire, alors ![]() Donc
Donc ![]() et donc
et donc ![]() Ceci montre que
Ceci montre que ![]() et l’injectivité de
et l’injectivité de ![]() est établie.
est établie.
Réciproquement, supposons ![]() injective et soit
injective et soit ![]() Alors
Alors ![]() et
et ![]() donc
donc ![]() c’est-à-dire
c’est-à-dire ![]() ou encore
ou encore ![]()
5 – Quelques exemples de nature théorique
Image d’une forme linéaire
Dans le premier exemple de la section 3, on a rencontré une forme linéaire surjective.
D’une manière générale, si ![]() est un
est un ![]() -espace vectoriel et si
-espace vectoriel et si ![]() est une forme linéaire, alors
est une forme linéaire, alors ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() c’est-à-dire
c’est-à-dire ![]() ou
ou ![]() Retenons ceci :
Retenons ceci :
Une forme linéaire est nécessairement nulle ou surjective.
Il n’y a pas de demi-mesure : soit tous les scalaires sont atteints par ![]() soit 0 est le seul scalaire atteint.
soit 0 est le seul scalaire atteint.
Concernant le noyau d’une forme linéaire, voir la section 6 plus bas.
Eléments propres
Considérons un ![]() -espace vectoriel et un endomorphisme
-espace vectoriel et un endomorphisme ![]() de
de ![]() Par définition, un scalaire
Par définition, un scalaire ![]() est une valeur propre de
est une valeur propre de ![]() lorsqu’il existe
lorsqu’il existe ![]() tel que
tel que ![]() Un tel vecteur
Un tel vecteur ![]() est appelé un vecteur propre associé à la valeur propre
est appelé un vecteur propre associé à la valeur propre ![]() L’ensemble des valeurs propres de
L’ensemble des valeurs propres de ![]() est une partie de
est une partie de ![]() appelée spectre de
appelée spectre de ![]() et notée
et notée ![]()
Si ![]() alors :
alors :
![]()
Lorsque ![]() est valeur propre de
est valeur propre de ![]() l’ensemble
l’ensemble ![]() est constitué du vecteur nul et des vecteurs propres associés à
est constitué du vecteur nul et des vecteurs propres associés à ![]()
On l’appelle le sous-espace vectoriel propre pour ![]() associé à
associé à ![]()
L’étude des « éléments propres » est au cœur de la réduction des endomorphismes, qui est une question centrale en algèbre linéaire.
A ce sujet, je vous invite à consulter les vidéos éléments propres d’un endomorphisme et étude spectrale de l’endomorphisme ![]()
Noyau d’une restriction
Noyau d’une restriction – Si ![]() et si
et si ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() on peut s’intéresser à la restriction de
on peut s’intéresser à la restriction de ![]() à
à ![]() qui est par définition l’application
qui est par définition l’application
![]()
![]()
Question
Soient ![]() un
un ![]() -espace vectoriel de dimension finie et
-espace vectoriel de dimension finie et ![]() des endomorphismes de
des endomorphismes de ![]()
Prouver que :
![]()
Une solution est donnée en annexe.
Noyau ou image d’un polynôme d’endomorphisme
Avant tout, si vous avez besoin d’une petite piqure de rappel au sujet des polynômes d’endomorphismes, je vous suggère de consulter les vidéos Polynômes d’endomorphisme (1) et Polynômes d’endomorphisme (2)
Il est utile de connaître le résultat suivant :
Lemme
Si ![]() est un endomorphisme et si
est un endomorphisme et si ![]() alors le noyau et l’image de
alors le noyau et l’image de ![]() sont stables par tout endomorphisme
sont stables par tout endomorphisme ![]() qui commute avec
qui commute avec ![]()
Preuve (cliquer pour déplier / replier)
Si ![]() et
et ![]() commute, alors
commute, alors ![]() et
et ![]() commutent pour tout
commutent pour tout ![]() et donc
et donc ![]() et
et ![]() commutent aussi. Ceci étant dit :
commutent aussi. Ceci étant dit :
- Pour montrer que
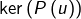 est stable par
est stable par 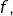 on se donne
on se donne 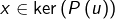 et l’on vérifie que
et l’on vérifie que 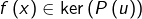 :
:![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left[P\left(u\right)\right]\left(f\left(x\right)\right) & = \left[P\left(u\right)\circ f\right]\left(x\right) \\& = \left[f\circ P\left(u\right)\right]\left(x\right) \\& = f\left(\left[P\left(u\right)\right]\left(x\right)\right) \\& = f\left(0_{E}\right) \\& = 0_{E}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-df6bd7a5b4c924757f5ad06c3bf860b0_l3.png)
- Pour montrer que
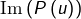 est stable par
est stable par 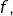 on se donne
on se donne 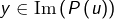 et l’on vérifie que
et l’on vérifie que 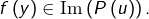 En posant
En posant ![Rendered by QuickLaTeX.com y=\left[P\left(u\right)\right]\left(x\right)](https://math-os.com/wp-content/ql-cache/quicklatex.com-f17adfec1ef05f3923b3c8f56a1bdb67_l3.png) pour un certain
pour un certain 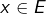 :
:![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}f\left(y\right) & = f\left(\left[P\left(u\right)\right]\left(x\right)\right) \\& = \left(f\circ P\left(u\right)\right)\left(x\right) \\& = \left(P\left(u\right)\circ f\right)\left(x\right) \\& = \left[P\left(u\right)\right]\left(f\left(x\right)\right) \\& \in \text{Im}\left(P\left(u\right)\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-23f74b9046c85b0fb54f82221e82b50f_l3.png)
Voici un exemple d’utilisation de ce résultat.
Exemple (dans l’exemple …)
Dans l’espace ![]() l’endomorphisme de dérivation ne possède pas de racine carrée.
l’endomorphisme de dérivation ne possède pas de racine carrée.
Notons ![]() l’endomorphisme de dérivation :
l’endomorphisme de dérivation :
![]()
Dans une vidéo qui sera prochainement mise en ligne, on présentera une application plus consistante, à savoir que pour toute famille d’endomorphismes diagonalisables qui commutent deux à deux, on peut trouver une base commune de diagonalisation.
6 – Hyperplans
Commençons par préciser le vocabulaire. Considérons un espace vectoriel ![]() et un sous-espace vectoriel
et un sous-espace vectoriel ![]() de
de ![]() .
.
Définition
On dit que ![]() est un hyperplan de
est un hyperplan de ![]() si
si ![]() possède une droite supplémentaire, autrement dit s’il existe
possède une droite supplémentaire, autrement dit s’il existe ![]() tel que :
tel que :
![]()
Si ![]() est de dimension finie, ceci revient à dire que
est de dimension finie, ceci revient à dire que ![]()
Mais lorsque ![]() est de dimension infinie, cette dernière formulation n’a pas de sens ! En revanche, on dispose de la caractérisation suivante, valable en dimension quelconque :
est de dimension infinie, cette dernière formulation n’a pas de sens ! En revanche, on dispose de la caractérisation suivante, valable en dimension quelconque :
Proposition
![]() est un hyperplan de
est un hyperplan de ![]() si, et seulement s’il existe une forme linéaire sur
si, et seulement s’il existe une forme linéaire sur ![]() , non nulle et de noyau
, non nulle et de noyau ![]() .
.
Preuve (cliquer pour déplier / replier)
Sens direct
Supposons l’existence d’une forme linéaire ![]() non nulle et de noyau
non nulle et de noyau ![]() .
.
Choisissons ![]() et montrons que tout
et montrons que tout ![]() s’écrit, de façon unique, sous la forme :
s’écrit, de façon unique, sous la forme :
![]()
![]()
![]()
![]()
![]()
Sens réciproque
Supposons maintenant l’existence d’un vecteur ![]() tel que
tel que ![]() .
.
On sait qu’on peut définir une application linéaire par ses restrictions à des sev supplémentaires. Construisons donc une forme linéaire ![]() en imposant
en imposant ![]() pour tout
pour tout ![]() et
et ![]()
Manifestement, ![]() n’est pas la forme linéaire nulle ! Il reste à constater que
n’est pas la forme linéaire nulle ! Il reste à constater que ![]()
L’inclusion ![]() est déjà évidente. Pour l’inclusion inverse, donnons-nous
est déjà évidente. Pour l’inclusion inverse, donnons-nous ![]() et prouvons que
et prouvons que ![]() Pour cela, on commence par décomposer
Pour cela, on commence par décomposer ![]() sous la forme
sous la forme ![]() avec
avec ![]() et
et ![]() Alors :
Alors :
![]()
7 – Equations linéaires
Définition
On appelle équation linéaire toute équation de la forme ![]() (et d’inconnue
(et d’inconnue ![]() ) où
) où ![]() sont deux espaces vectoriels sur un même corps
sont deux espaces vectoriels sur un même corps ![]() ,
, ![]() une application linéaire de
une application linéaire de ![]() dans
dans ![]() et
et ![]() un vecteur de
un vecteur de ![]() .
.
L’ensemble ![]() des solutions est de l’une des deux formes suivantes :
des solutions est de l’une des deux formes suivantes :
![]()
![]()
- Résolution de l’équation homogène associée
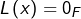
- Recherche d’une solution particulière
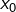

ATTENTION … Il convient d’interpréter correctement l’écriture :
![]()
On note ainsi l’ensemble des vecteurs de la forme ![]() où
où ![]() est arbitraire.
est arbitraire.
Donnons deux exemples.
Suite numériques vérifiant une relation de récurrence linéaire
Les suites ![]() vérifiant :
vérifiant :
![]()
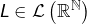 est l’endomorphisme défini par :
est l’endomorphisme défini par :![Rendered by QuickLaTeX.com \[L\left(u\right)=v\qquad\text{avec }\forall n\in\mathbb{N},\thinspace v_{n}=u_{n+1}-u_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2961678897d5d81e5c2698b2a74cdfe3_l3.png)
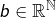 est la suite définie par
est la suite définie par 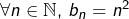
Solutions d’une équation différentielle linéaire
Les applications deux fois dérivables ![]() vérifiant :
vérifiant :
![]()
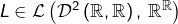 est l’application linéaire définie par :
est l’application linéaire définie par :![Rendered by QuickLaTeX.com \[L\left(f\right)=g\qquad\text{avec }\forall t\in\mathbb{R},\thinspace g\left(t\right)=t^{2}\thinspace f''\left(t\right)+f\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c77735f88d9e7f2113352f61d667c2f0_l3.png)
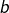 est l’application constante
est l’application constante 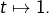
8 – Le théorème du rang
Théorème et Définition
Etant donnés deux ![]() -espaces vectoriels
-espaces vectoriels ![]() et
et ![]() si
si ![]() de dimension finie et si
de dimension finie et si ![]() est une application linéaire de
est une application linéaire de ![]() dans
dans ![]() alors :
alors :
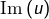 est de dimension finie
est de dimension finie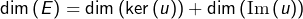 (formule du rang)
(formule du rang)
L’entier ![]() est appelé « rang » de
est appelé « rang » de ![]() et noté
et noté ![]()
La démonstration est courte et instructive, alors on en profite 🙂
Preuve (cliquer pour déplier / replier)
Avant tout, il faut observer que ![]() est évidemment de dimension finie si c’est déjà le cas de
est évidemment de dimension finie si c’est déjà le cas de ![]() Et sinon, on revient à la définition : rappelons qu’un espace vectoriel
Et sinon, on revient à la définition : rappelons qu’un espace vectoriel ![]() est dit « de dimension finie » lorsqu’il existe une famille finie et génératrice de
est dit « de dimension finie » lorsqu’il existe une famille finie et génératrice de ![]() Or par hypothèse, il existe une famille finie
Or par hypothèse, il existe une famille finie ![]() qui est génératrice de
qui est génératrice de ![]() Pour tout
Pour tout ![]() il existe
il existe ![]() tel que
tel que ![]() et il existe des scalaires
et il existe des scalaires ![]() tels que :
tels que :
![Rendered by QuickLaTeX.com \[x=\sum_{i=1}^{n}\lambda_{i}e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-641371eb24b3fa26111b4bfd251c5b6d_l3.png)
![Rendered by QuickLaTeX.com \[y=\sum_{i=1}^{n}\lambda_{i}\thinspace u\left(e_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60de91d83a6bafa78dfeb25d7b9d132b_l3.png)
Pour établir la formule du rang, la clef consiste à voir que ![]() est la dimension d’un sev supplémentaire de
est la dimension d’un sev supplémentaire de ![]() dans
dans ![]() Il suffit donc de montrer que
Il suffit donc de montrer que ![]() est isomorphe à un tel sev.
est isomorphe à un tel sev.
Soit donc ![]() un sev de
un sev de ![]() tel que :
tel que :
![]()
![]()

Attention, cette application ne doit pas être confondue avec ![]() Elle est, en quelque sorte, une « bi-restriction » de
Elle est, en quelque sorte, une « bi-restriction » de ![]() dans la mesure où elle a été obtenue en « rétrécissant » les espaces de départ et d’arrivée.
dans la mesure où elle a été obtenue en « rétrécissant » les espaces de départ et d’arrivée.
Il s’agit de montrer que ![]() est un isomorphisme, c’est-à-dire que :
est un isomorphisme, c’est-à-dire que :
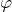 est linéaire
est linéaire est injective
est injective est surjective
est surjective
La linéarité de ![]() ne fait aucun doute, puisque
ne fait aucun doute, puisque ![]() est linéaire !
est linéaire !
Pour montrer que ![]() est injective, il suffit (cf. section 4) de voir que son noyau est réduit à
est injective, il suffit (cf. section 4) de voir que son noyau est réduit à ![]()
Or, d’après ce qui a été dit au paragraphe 3 de la section 5 et vu que la somme ![]() est directe :
est directe :
![]()
Enfin, si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() puis, en décomposant
puis, en décomposant ![]() selon la somme directe, il existe
selon la somme directe, il existe ![]() et
et ![]() tels que
tels que ![]() d’où par linéarité :
d’où par linéarité : ![]() Et cette dernière égalité peut encore s’écrire
Et cette dernière égalité peut encore s’écrire ![]() La surjectivité de
La surjectivité de ![]() est établie.
est établie.
Voici un corollaire classique et d’usage courant :
Corollaire
Si ![]() sont des
sont des ![]() -espaces vectoriels de même dimension finie et si
-espaces vectoriels de même dimension finie et si ![]() alors :
alors :
![]()
Le théorème rang a été utilisé dans l’exemple 2 de la section 3 et le sera de nouveau dans l’annexe. Voici un autre exemple :
Deux projecteurs assez voisins sont de même rang
On considère un ![]() espace vectoriel normé de dimension finie. La norme en vigueur sur
espace vectoriel normé de dimension finie. La norme en vigueur sur ![]() est notée
est notée ![]() et l’on munit
et l’on munit ![]() de la norme (dite « norme d’opérateur ») définie par :
de la norme (dite « norme d’opérateur ») définie par :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall f\in\mathcal{L}\left(E\right),\:\left\Vert f\right\Vert_{\text{op}}=\displaystyle{\sup_{x\in E-\left\{0_{E}\right\}}\frac{\left\Vert f\left(x\right)\right\Vert}{\left\Vert x\right\Vert}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ae7bada908b799e53b0153dab333b3e_l3.png)
![]()
![]()
![]()
Et voici un exemple d’utilisation du corollaire énoncé plus haut :
Isomorphisme d’interpolation
Etant donnés un entier ![]() et des scalaires
et des scalaires ![]() tous distincts, l’application
tous distincts, l’application
![]()
En effet, après avoir constaté la linéarité de ![]() on examine son noyau …
on examine son noyau …
Si ![]() alors chacun des scalaires
alors chacun des scalaires ![]() est une racine de
est une racine de ![]() dans
dans ![]() d’où l’on déduit qu’il existe
d’où l’on déduit qu’il existe ![]() tel que :
tel que :
![]()
C’est maintenant qu’on invoque le corollaire : puisque les espaces vectoriels ![]() et
et ![]() sont de même dimension, alors
sont de même dimension, alors ![]() est aussi surjective, d’où la conclusion.
est aussi surjective, d’où la conclusion.
9 – Quotienter par le noyau
La théorie des espaces vectoriels quotients n’est plus enseignée depuis belle-lurette, ni en premier cycle universitaire ni en classes préparatoires. Il va donc falloir expliquer un peu de quoi il retourne …
Dans ce qui suit, on considère un ![]() -espace vectoriel
-espace vectoriel ![]() ainsi qu’un sev
ainsi qu’un sev ![]() de
de ![]() et l’on définit sur
et l’on définit sur ![]() une relation binaire, notée
une relation binaire, notée ![]() en posant :
en posant :
![]()
Il est facile de voir qu’il s’agit d’une relation d’équivalence. Voir à ce sujet la vidéo Théorème de Lagrange et Ordre d’un élément
Si ![]() alors la classe d’équivalence de
alors la classe d’équivalence de ![]() est (par définition) :
est (par définition) :
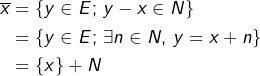
En particulier, ![]() n’est autre que la classe du vecteur nul.
n’est autre que la classe du vecteur nul.
L’ensemble des classes d’équivalence est noté ![]()
On va maintenant définir deux opérations (pour les puristes : une opération interne et une opération externe à opérateurs dans ![]() :
:
- si
 et
et  sont deux classes d’équivalence, alors en choisissant
sont deux classes d’équivalence, alors en choisissant 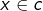 et
et 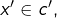 on pose :
on pose :![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$c+c'=\overline{x+x'}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d99f0d957ab511097a02979734590a9_l3.png)
- si
 est une classe d’équivalence et si
est une classe d’équivalence et si 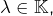 alors en choisissant
alors en choisissant 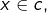 on pose :
on pose :![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\lambda c=\overline{\lambda x}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f26fdf3cac62726f80070757aa3f952a_l3.png)
Comme toujours dans ce genre de situation, il faut s’assurer que :
- ces définitions ont un sens, c’est-à-dire qu’en dépit des apparences :
- la classe
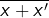 ne dépend pas des représentants
ne dépend pas des représentants  et
et 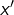 choisis dans
choisis dans  et dans
et dans 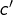
- la classe
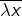 ne dépend pas du représentant
ne dépend pas du représentant  choisi dans
choisi dans 
- la classe
- les opérations d’addition et de multiplication par un scalaire, qui viennent d’être définies, confèrent à
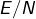 une structure de
une structure de 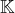 -espace vectoriel.
-espace vectoriel.
Je vous passe les détails de ces vérifications (qui ne soulèvent aucune difficulté et constituent un bon exercice !), moyennant quoi on dispose désormais de l’espace vectoriel ![]() (appelé espace quotient de
(appelé espace quotient de ![]() par
par ![]() ).
).
Proposition
L’espace ![]() est isomorphe à tout supplémentaire de
est isomorphe à tout supplémentaire de ![]() dans
dans ![]()
Preuve (cliquer pour déplier / replier)
Il suffit d’adapter légèrement la preuve de la 2ème partie du théorème du rang.Soit ![]() tel que
tel que ![]() L’application
L’application
![]()
![]()
Elle est aussi injective, car :
![]()
En outre, ![]() est surjective car si
est surjective car si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() . On peut écrire
. On peut écrire ![]() avec
avec ![]() et
et ![]() On voit alors que
On voit alors que ![]()
Corollaire
Si ![]() alors les espaces
alors les espaces ![]() et
et ![]() sont isomorphes.
sont isomorphes.
Preuve (cliquer pour déplier / replier)
En effet, si ![]() désigne un supplémentaire de
désigne un supplémentaire de ![]() dans
dans ![]() on sait :
on sait :
- que
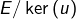 est isomorphe à
est isomorphe à 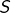 d’après le théorème précédent,
d’après le théorème précédent, - que
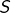 est isomorphe à
est isomorphe à 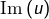 d’après la deuxième partie du théorème du rang.
d’après la deuxième partie du théorème du rang.
d’où le résultat.
Donnons un exemple d’utilisation de ce corollaire.
Exemple
Supposons ![]() de dimension finie et soit
de dimension finie et soit ![]() L’ensemble :
L’ensemble :
![]()
Il est déjà clair que ![]() c’est-à-dire :
c’est-à-dire : ![]()
Pour déterminer cette dimension, l’idée est d’établir un isomorphisme entre ![]() et un espace vectoriel dont la dimension est connue.
et un espace vectoriel dont la dimension est connue.
Etant donné ![]() la condition
la condition ![]() équivaut à
équivaut à ![]() On comprend ainsi que, pour définir un élément
On comprend ainsi que, pour définir un élément ![]() de
de ![]() il est nécessaire et suffisant d’en connaître la restriction à un supplémentaire de
il est nécessaire et suffisant d’en connaître la restriction à un supplémentaire de ![]() dans
dans ![]()
Une façon de formaliser cette idée consiste à s’intéresser à l’application
![]()
Cette définition tient la route puisque, si ![]() et
et ![]() sont deux représentants d’une même classe
sont deux représentants d’une même classe ![]() alors
alors ![]() et donc
et donc ![]()
La linéarité de ![]() se prouve de manière « automatique » … en effet, si
se prouve de manière « automatique » … en effet, si ![]() et
et ![]() alors pour tout
alors pour tout ![]() et en notant
et en notant ![]() :
:
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left[\Phi\left(\lambda u+v\right)\right]\left(c\right) & = \left(\lambda u+v\right)\left(x\right)\\& = \lambda\thinspace u\left(x\right)+v\left(x\right)\\& = \lambda\thinspace\left[\Phi\left(u\right)\right]\left(c\right)+\left[\Phi\left(v\right)\right]\left(c\right)\\& = \left(\lambda\thinspace\Phi\left(u\right)+\Phi\left(v\right)\right)\left(c\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-00eec7749f9cbe353dbed503b6aa4931_l3.png)
Enfin (et surtout),
- Injectivité – si
 alors, pour tout
alors, pour tout 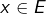 :
:
c’est-à-dire![Rendered by QuickLaTeX.com \[u\left(x\right)=\left[\Phi\left(u\right)\right]\left(\overline{x}\right)=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b44b474946c68de6cd0fdac003e2480f_l3.png)
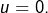
- Surjectivité – pour tout
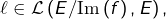 l’application
l’application
est un endomorphisme de![Rendered by QuickLaTeX.com \[u:E\rightarrow E,\thinspace x\mapsto\ell\left(\overline{x}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c09c96ca417cbe199b085fea5b1d8aba_l3.png)
 vérifiant
vérifiant 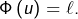
Au final :
![]()
![]()
Annexe : réponses aux questions
Détermination du noyau et de l’image de l’application linéaire
![]()
D’une part :
![]()
![]()
En outre :
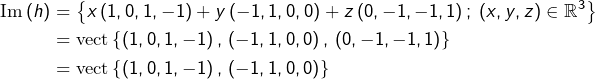
![]()
Et comme la famille ![]() est libre, c’est une base du plan vectoriel
est libre, c’est une base du plan vectoriel ![]()
Détermination de l’image de l’endomorphisme ![]()
On note comme d’habitude ![]() l’espace des polynômes de degré inférieur ou égal à
l’espace des polynômes de degré inférieur ou égal à ![]()
On sait que ![]() puisque la famille
puisque la famille ![]() est une base de cet espace.
est une base de cet espace.
Si ![]() et si
et si ![]() n’est pas constant, alors
n’est pas constant, alors ![]()
Et si ![]() est constant, on sait que
est constant, on sait que ![]() Ceci prouve que
Ceci prouve que ![]()
On dispose donc de l’application ![]() que l’on peut noter
que l’on peut noter ![]()
Comme
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\text{rg}\left(\Delta_{n}\right) & = \dim\left(\mathbb{R}_{n}\left[X\right]\right)-\dim\left(\ker\left(\Delta_{n}\right)\right)\\& =\left(n+1\right)-1\\& =n\\& =\dim\left(\mathbb{R}_{n-1}\left[X\right]\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-da9ce1491f46f02a4b969dfb0a9a598b_l3.png)
Il s’ensuit que ![]() autrement dit :
autrement dit : ![]() est surjective.
est surjective.
Finalement ![]() est surjective : en effet, pour tout
est surjective : en effet, pour tout ![]() il suffit de choisir
il suffit de choisir ![]() de telle sorte que
de telle sorte que ![]() et d’invoquer la surjectivité de
et d’invoquer la surjectivité de ![]()
Deux matrices carrées semblables ont la même trace.
On va utiliser la propriété suivante (qui repose sur une simple interversion de sommes) :
![]()
Soient ![]() deux matrices semblables, ce qui signifie qu’il existe
deux matrices semblables, ce qui signifie qu’il existe ![]() vérifiant :
vérifiant :
![]()
Un exemple de fonction numérique définie sur un intervalle et ne possédant aucune primitive.
Considérons
![Rendered by QuickLaTeX.com \[f:\left[-1,1\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}-1 & \text{si }-1\leqslant x<0\\\\1 & \text{si }0\leqslant x\leqslant1\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-227d22735dc5dbfa10d8fddf4f695cbd_l3.png)
![]()
![]()
Comme ![]() est notamment continue en
est notamment continue en ![]() alors :
alors :
![]()
![]()
Mais on sait bien que la fonction valeur absolue n’est pas dérivable en ![]() ce qui entraîne la même propriété pour
ce qui entraîne la même propriété pour ![]() : contradiction !
: contradiction !
Majoration de la dimension du noyau de la somme de deux endomorphismes.
Considérons la restriction ![]() de
de ![]() au noyau de
au noyau de ![]() :
:
![]()
D’après la remarque générale signalée au troisième point de la section 5 :
![]()
On observe que si ![]() alors
alors ![]() et donc
et donc ![]()
Réciproquement, si ![]() alors
alors ![]() et donc
et donc ![]() Par conséquent :
Par conséquent :
![]()
Par ailleurs, si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() mais alors :
mais alors :
![]()
![]()
On applique maintenant la formule du rang, ce qui donne :
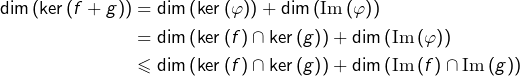
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonjour,
Pour l’endomorphisme défini par
défini par 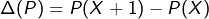 , on peut déterminer l’image en décomposant selon l’écriture générale des polynômes de
, on peut déterminer l’image en décomposant selon l’écriture générale des polynômes de ![Rendered by QuickLaTeX.com \mathbb{R}[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-06ab68fe7957341fe021e7b77512ca37_l3.png) tq:
tq: 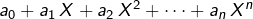 . En développant, on aboutit à la formule suivante:
. En développant, on aboutit à la formule suivante:
auquel cas on voit que c’est l’ensemble des polynômes de degré inférieur ou égal à . Est-ce équivalent à la demonstration du cours ?
. Est-ce équivalent à la demonstration du cours ?
Bonjour Joseph,
On peut en effet exprimer comme vous le faites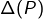 dans la base canonique et constater que si
dans la base canonique et constater que si ![Rendered by QuickLaTeX.com P\in\mathbb{R}_n[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-84687572d15dacc3d1e3a981b13ba6c0_l3.png) avec
avec 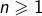 , alors
, alors ![Rendered by QuickLaTeX.com \Delta(P)\in\mathbb{R}_{n-1}[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-076ac2f96a7cf4f4692d313e9309b3d9_l3.png) , mais cet argument doit être légèrement étoffé pour expliquer que l’on atteint bien tout l’espace
, mais cet argument doit être légèrement étoffé pour expliquer que l’on atteint bien tout l’espace ![Rendered by QuickLaTeX.com \mathbb{R}_{n-1}[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e2dbdebb0c440431e19681d861a7904_l3.png) , moyennant quoi on pourra conclure que
, moyennant quoi on pourra conclure que 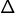 induit une application linéaire surjective de
induit une application linéaire surjective de ![Rendered by QuickLaTeX.com \mathbb{R}_n[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-87e0c961f301bc0d2a500f536a0e94b5_l3.png) vers
vers ![Rendered by QuickLaTeX.com \mathbb{R}_{n-1}[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e2dbdebb0c440431e19681d861a7904_l3.png) . Et comme ceci vaut pour tout
. Et comme ceci vaut pour tout 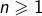 , on peut alors conclure que
, on peut alors conclure que  est surjectif.
est surjectif.