
On présente ici diverses méthodes permettant de définir une application linéaire. Elles sont assorties d’exemples détaillés.
Précisons que cet article est assez synthétique et s’adresse à des lecteurs ayant déjà une certaine pratique de l’algèbre linéaire.
Avant de commencer, rappelons ce qu’est une application linéaire et donnons des exemples.
1 – Qu’est-ce qu’une application linéaire ?
Définition
Etant donnés deux espaces vectoriels ![]() et
et ![]() sur un même corps
sur un même corps ![]() une application
une application ![]() est dite linéaire lorsque l’image d’une combinaison linéaire de vecteurs de
est dite linéaire lorsque l’image d’une combinaison linéaire de vecteurs de ![]() est égale la combinaison linéaire de leurs images respectives, avec les mêmes coefficients.
est égale la combinaison linéaire de leurs images respectives, avec les mêmes coefficients.
En symboles, cette condition devient :
![]()
![Rendered by QuickLaTeX.com \[u\left(\sum_{i=1}^{n}\lambda_{i}x_{i}\right)=\sum_{i=1}^{n}\lambda_{i}\thinspace u\left(x_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-24f086b251f58d0fdf29eddd48c421ab_l3.png)
![]()
Exemple fondamental 1
Fixons un entier ![]() Il est clair que, pour tout
Il est clair que, pour tout ![]() l’application
l’application
![Rendered by QuickLaTeX.com \[\mathbb{K}^{q}\rightarrow\mathbb{K},\:\left(t_{1},\cdots,t_{q}\right)\mapsto\sum_{j=1}^{q}\alpha_{j}t_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6892bc5e0422b7b7b0c19caf984b1a8e_l3.png)
Terminologie
Lorsque l’espace d’arrivée d’une application linéaire est ![]() on parle de forme linéaire.
on parle de forme linéaire.
Réciproquement, toute forme linéaire sur ![]() est de ce type ! En effet :
est de ce type ! En effet :
Notons ![]() la base canonique de
la base canonique de ![]()
Pour chaque ![]()
![]() désigne donc le
désigne donc le ![]() uplet de scalaires dont les composantes sont toutes nulles, à l’exception de la
uplet de scalaires dont les composantes sont toutes nulles, à l’exception de la ![]() ème, qui vaut 1 :
ème, qui vaut 1 :

Soit ![]() une forme linéaire. Pour tout
une forme linéaire. Pour tout ![]() :
:
![]()
![]()
Exemple fondamental 2
Soient ![]() deux entiers naturels non nuls et
deux entiers naturels non nuls et ![]() une application linéaire.
une application linéaire.
On peut définir des applications ![]() avec
avec ![]() en décrétant que, pour tout
en décrétant que, pour tout ![]()
![]() désigne la
désigne la ![]() ème coordonnée du vecteur
ème coordonnée du vecteur ![]() dans la base canonique de
dans la base canonique de ![]()
Plus simplement dit :
![]()
Chacune d’elles est d’évidence une forme linéaire. D’après l’exemple fondamental 1, il existe des scalaires ![]()
![]() et
et ![]() tels que :
tels que :
![]()
Réciproquement, toute application de
Au passage, notons qu’on est à deux doigts du formalisme matriciel ! La matrice de ![]() relativement aux bases canoniques de
relativement aux bases canoniques de ![]() et
et ![]() est en effet :
est en effet :
![Rendered by QuickLaTeX.com \[\left[\begin{array}{ccccc}\beta_{1,1} & \beta_{1,2} & \cdots & \cdots & \beta_{1,q}\\\beta_{2,1} & \beta_{2,2} & \cdots & \cdots & \beta_{2,q}\\\vdots & \vdots & & & \vdots\\\beta_{p,1} & \beta_{p,2} & \cdots & \cdots & \beta_{p,q}\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-101cc2df91fea8304d6b4d9eaddc61cd_l3.png)
Exemple fondamental 3
Soient ![]() deux réels tels que
deux réels tels que ![]() et soit
et soit ![]() une application continue.
une application continue.
Notons ![]() le
le ![]() espace vectoriel des applications continues de
espace vectoriel des applications continues de ![]() dans
dans ![]() et posons :
et posons :
![]()

Il existe des formes linéaires sur ![]() qui ne sont pas de ce type !
qui ne sont pas de ce type !
C’est le cas de ![]() .
.
Cette forme linéaire est appelée évaluation en ![]() .
.
Sauriez-vous prouver qu’il n’existe aucune application ![]() telle que
telle que ![]() ?
?
→ Réponse en annexe
2 – Sept applications linéaires explicitement définies
Pour définir une application linéaire, le plus simple consiste à spécifier (via une formule explicite) l’image de chaque vecteur de l’espace de départ.
Exemple 1
Exemple 2
Exemple 3
Notons ![]() l’espace des applications continues de
l’espace des applications continues de ![]() dans
dans ![]() L’application
L’application
![]()
Exemple 4
Soit ![]() un ensemble non vide quelconque et soit
un ensemble non vide quelconque et soit ![]()
Soit, par ailleurs, un ![]() espace vectoriel
espace vectoriel ![]()
On note ![]() l’espace vectoriel de toutes les applications de
l’espace vectoriel de toutes les applications de ![]() vers
vers ![]() L’application :
L’application :
![]()
Terminologie
Lorsque les espaces de départ et d’arrivée d’une application linéaire sont confondus, on parle d’endomorphisme.
Exemple 5
Notons ![]() l’espace des toutes les applications de
l’espace des toutes les applications de ![]() dans
dans ![]() et soit
et soit ![]()
L’application :
![]()
Exemple 6
Notons ![]() l’espace des suites réelles convergentes. L’application :
l’espace des suites réelles convergentes. L’application :
![]()
Exemple 7
Notons ![]() l’espace des « suites réelles de carré sommables », c’est-à-dire des suites réelles
l’espace des « suites réelles de carré sommables », c’est-à-dire des suites réelles ![]() pour lesquelles la série
pour lesquelles la série ![]() converge. L’application :
converge. L’application :
![Rendered by QuickLaTeX.com \[\theta:H\rightarrow\mathbb{R},\thinspace u\mapsto\sum_{n=0}^{\infty}\frac{u_{n}}{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-10078b5440625c79924b81d39a4f5b2a_l3.png)
Cette liste pourrait être poursuivie, mais elle suffit largement pour s’apercevoir de la diversité des possibilités. Passons maintenant aux choses sérieuses…
3 – Définition par l’image d’une base
Considérons deux ![]() espaces vectoriels
espaces vectoriels ![]() et supposons
et supposons ![]() de dimension finie.
de dimension finie.
Notons ![]()
Théorème (T)
Etant données une base ![]() de
de ![]() et une famille
et une famille ![]() de
de ![]() vecteurs de
vecteurs de ![]() il existe une application linéaire
il existe une application linéaire ![]() et une seule vérifiant :
et une seule vérifiant :
![]()
Autrement dit, une application linéaire est parfaitement définie par la donnée des images des vecteurs d’une base.
La preuve de ce théorème est détaillée en annexe, à la fin de l’article.
Voici un exemple d’utilisation.
Endomorphismes anti-involutifs en dimension paire
Considérons un ![]() espace vectoriel
espace vectoriel ![]() de dimension finie
de dimension finie ![]() et supposons qu’il existe un endomorphisme
et supposons qu’il existe un endomorphisme ![]() tel que
tel que ![]() (c’est-à-dire :
(c’est-à-dire : ![]()
Le déterminant d’une composée d’endomorphismes étant égal au produit des déterminants des facteurs, on voit que :
![]()
La réciproque de cette propriété est encore vraie :
Proposition
Si ![]() un
un ![]() espace vectoriel de dimension paire, alors il existe un endomorphisme
espace vectoriel de dimension paire, alors il existe un endomorphisme ![]() tel que
tel que ![]()
Notons ![]() et donnons-nous une base
et donnons-nous une base ![]() de
de ![]()
D’après le théorème (T), on définit un endomorphisme ![]() en imposant :
en imposant :
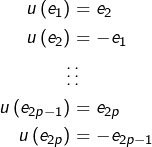
Pour tout ![]() de deux choses l’une :
de deux choses l’une :
➣ si ![]() est pair, alors :
est pair, alors :
![]()
➣ si
![]()
Les endomorphismes ![]() et
et ![]() coïncident sur une base, ils sont donc égaux.
coïncident sur une base, ils sont donc égaux.
Remarque
Dans cet exemple, le corps de base était ![]() ce qui a permis de dire que
ce qui a permis de dire que ![]() est positif ou nul.
est positif ou nul.
Une telle affirmation n’aurait eu aucun sens si ![]() D’ailleurs, dans ce cas, l’existence d’endomorphismes « anti-involutifs » est assurée sans aucune contrainte de parité : il suffit de considérer l’homothétie de rapport
D’ailleurs, dans ce cas, l’existence d’endomorphismes « anti-involutifs » est assurée sans aucune contrainte de parité : il suffit de considérer l’homothétie de rapport ![]() (avec bien sûr
(avec bien sûr ![]()
4 – Définition par les restrictions à des sous-espaces supplémentaires
Considérons deux ![]() espaces vectoriels
espaces vectoriels ![]() ainsi que deux sous-espaces
ainsi que deux sous-espaces ![]() de
de ![]() tels que
tels que ![]() (rappelons ce que cela signifie : tout vecteur de
(rappelons ce que cela signifie : tout vecteur de ![]() peut s’écrire, de manière unique, comme la somme de deux vecteurs, l’un appartenant à
peut s’écrire, de manière unique, comme la somme de deux vecteurs, l’un appartenant à ![]() et l’autre à
et l’autre à ![]()
Théorème (T’)
Etant données des applications linéaires ![]() et
et ![]() il existe une application linéaire
il existe une application linéaire ![]() et une seule telle que :
et une seule telle que :
![]()
Autrement dit, une application linéaire est parfaitement déterminée par la donnée de ses restrictions (linéaires !) à deux sous-espaces supplémentaires.
Là encore, laissons de côté la démonstration (le lecteur intéressé la lira en annexe) et donnons deux exemples d’utilisation.
Un lemme de Noether
Considérons trois ![]() espaces vectoriels
espaces vectoriels ![]() et
et ![]() ainsi que deux applications linéaires
ainsi que deux applications linéaires ![]() et
et ![]()
Il est évident que s’il existe ![]() vérifiant
vérifiant ![]() alors
alors ![]()
En effet, pour tout vecteur ![]() :
:
![]()
Proposition
Avec les notations précédentes, si ![]() alors il existe une application linéaire
alors il existe une application linéaire ![]() telle que
telle que ![]()
Si une telle application ![]() existe, elle devra vérifier
existe, elle devra vérifier ![]() pour tout
pour tout ![]() On voit dans cette condition que
On voit dans cette condition que ![]() n’est appliquée qu’à des vecteurs appartenant à l’image de
n’est appliquée qu’à des vecteurs appartenant à l’image de ![]() Ceci suggère de considérer un supplémentaire
Ceci suggère de considérer un supplémentaire ![]() de
de ![]() dans
dans ![]() et de construire une application linéaire
et de construire une application linéaire ![]() en spécifiant ses restrictions à
en spécifiant ses restrictions à ![]() et à
et à ![]()
Pour la restriction à ![]() le plus simple consiste à prendre l’application nulle.
le plus simple consiste à prendre l’application nulle.
Pour la restriction à ![]() il faut faire attention…
il faut faire attention…
Si ![]() en posant
en posant ![]() avec
avec ![]() , il faudra qu’on ait
, il faudra qu’on ait ![]() .
.
En d’autres termes, il faut définir la restriction de ![]() à
à ![]() en associant à tout
en associant à tout ![]() l’image par
l’image par ![]() de l’un quelconque de ses antécédents par
de l’un quelconque de ses antécédents par ![]()
Le problème de cette formulation est que le résultat semble dépendre de l’antécédent choisi !
Fort heureusement, il n’en est rien; car si ![]() sont deux antécédents par
sont deux antécédents par ![]() du même
du même ![]() alors
alors ![]() donc (par hypothèse)
donc (par hypothèse) ![]() et finalement
et finalement ![]()
En résumé, il est licite de définir ![]() en décrétant que :
en décrétant que :
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{c}\forall y\in\text{Im}\left(u\right),\thinspace v\left(y\right)=u\left(x\right)\text{ avec }x\in u^{-1}\left(\left\{ y\right\} \right)\\\\\forall s\in S,\thinspace v\left(s\right)=0_{G}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f9a98a29861a87052ee23d190cd1ef18_l3.png)
Dimension d’un espace d’endomorphismes
Considérons ici un ![]() -espace vectoriel
-espace vectoriel ![]() de dimension finie
de dimension finie ![]() et endomorphisme
et endomorphisme ![]()
L’ensemble ![]() est un
est un ![]() -espace vectoriel : c’est clairement un sous-espace de
-espace vectoriel : c’est clairement un sous-espace de ![]()
Que peut-on dire de la dimension de ![]() ? Elle est évidemment majorée par
? Elle est évidemment majorée par ![]() mais à quoi est-elle égale ?
mais à quoi est-elle égale ?
Comme on va le voir, il est possible d’exprimer ![]() en fonction de
en fonction de ![]() et
et ![]()
Pour cela, observons qu’étant donné un endomorphisme ![]() la condition
la condition ![]() signifie que la restriction de
signifie que la restriction de ![]() à
à ![]() est nulle.
est nulle.

Moralement, se donner un élément de ![]() semble être équivalent à se donner une application linéaire de
semble être équivalent à se donner une application linéaire de ![]() vers
vers ![]() où
où ![]() désigne un supplémentaire de
désigne un supplémentaire de ![]() dans
dans ![]()
Terminologie
Lorsqu’une application linéaire est bijective, on parle d’isomorphisme.
Deux ![]() -espaces vectoriels sont dits isomorphes lorsqu’il existe un isomorphisme de l’un vers l’autre. Dans ce cas, si l’un des deux espaces est de dimension finie, alors l’autre aussi et les dimensions sont égales.
-espaces vectoriels sont dits isomorphes lorsqu’il existe un isomorphisme de l’un vers l’autre. Dans ce cas, si l’un des deux espaces est de dimension finie, alors l’autre aussi et les dimensions sont égales.
Afin de valider l’idée précédente, prouvons que ![]() est isomorphe à
est isomorphe à ![]()
Ceci entraînera que ![]() c’est-à-dire (vu que
c’est-à-dire (vu que ![]() et d’après la formule du rang) :
et d’après la formule du rang) :
![]()
L’application :
![]()
Il suffit pour conclure de prouver que ![]() est bijective.
est bijective.
➣ Injectivité
Si ![]() alors d’une part
alors d’une part ![]() pour tout
pour tout ![]() (définition du noyau d’une application linéaire) et d’autre part
(définition du noyau d’une application linéaire) et d’autre part ![]() pour tout
pour tout ![]() (par définition de
(par définition de ![]()
Comme ![]() il en résulte que
il en résulte que ![]() est l’endomorphisme nul.
est l’endomorphisme nul.
➣ Surjectivité
Soit ![]() On peut définir, grâce au théorème (T’), un endormorphisme
On peut définir, grâce au théorème (T’), un endormorphisme ![]() en spécifiant ses restrictions à
en spécifiant ses restrictions à ![]() et à
et à ![]() :
:
![]()
Annexe : quelques explications
1 – Question finale / Exemple fondamental 3
Il s’agissait de prouver ceci :
Proposition
Il n’existe aucune application continue ![]() telle que :
telle que :
![]()
Supposons le contraire et choisissons pour ![]() l’application
l’application ![]() Alors :
Alors :
![]()
![]()
Ceci impose, dans un premier temps, ![]() pour tout
pour tout ![]() Puis, comme
Puis, comme ![]() est continue en
est continue en ![]() on voit que
on voit que ![]()
Bref, ![]() est nécessairement l’application nulle.
est nécessairement l’application nulle.
Mais ceci est absurde, puisqu’il existe évidemment des applications continues sur ![]() qui ne s’annulent pas en
qui ne s’annulent pas en ![]()
2 – Preuve du théorème (T)
Dans ce qui suit, on notera ![]() la
la ![]() ème forme coordonnée (pour chaque
ème forme coordonnée (pour chaque ![]() c’est-à-dire la forme linéaire qui, à chaque
c’est-à-dire la forme linéaire qui, à chaque ![]() associe sa
associe sa ![]() ème coordonnée dans la base
ème coordonnée dans la base ![]() .
.
Raisonnons par analyse-synthèse. Si ![]() convient, alors pour tout
convient, alors pour tout ![]() vu que :
vu que :
![Rendered by QuickLaTeX.com \[x=\sum_{i=1}^{n}e_{i}^{\star}\left(x\right)\thinspace e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-032336d488fdf8c4918757b4ecfcaea1_l3.png)
![Rendered by QuickLaTeX.com \[u\left(x\right)=\sum_{i=1}^{n}e_{i}^{\star}\left(x\right)\thinspace u\left(e_{i}\right)=\sum_{i=1}^{n}e_{i}^{\star}\left(x\right)\thinspace f_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-977a35cafc72dc7cfed2b56051d2e9cf_l3.png)
Pour l’existence, il suffit de constater que l’application ![]() ainsi définie fait l’affaire. Elle est en effet linéaire (parce que les
ainsi définie fait l’affaire. Elle est en effet linéaire (parce que les ![]() le sont) et de plus, pour tout
le sont) et de plus, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[u\left(e_{j}\right)=\sum_{i=1}^{n}e_{i}^{\star}\left(e_{j}\right)\thinspace f_{i}=f_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4845c923b50465e23d131df23307079e_l3.png)
![]()
3 – Preuve du théorème (T’)
On sait que, pour tout ![]() il existe un unique couple
il existe un unique couple ![]() tel que
tel que ![]()
Notons ![]() l’application
l’application ![]() (c’est la première projection) et définissons
(c’est la première projection) et définissons ![]() de manière analogue.
de manière analogue.
Les applications ![]() et
et ![]() sont linéaires. Détaillons cela. Etant donné un couple
sont linéaires. Détaillons cela. Etant donné un couple ![]() de vecteurs de
de vecteurs de ![]() ainsi qu’un scalaire
ainsi qu’un scalaire ![]() on peut écrire :
on peut écrire :
![]()
![]()
![]()
![]()
![]()
Ces préliminaires étant posés, nous allons encore, comme dans la preuve du théorème [T], procéder par analyse-synthèse.
Analyse
Si ![]() convient, alors pour tout
convient, alors pour tout ![]() :
:
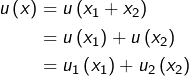
![]()
Synthèse
Réciproquement, si ![]() est ainsi définie, alors elle est linéaire (car
est ainsi définie, alors elle est linéaire (car ![]()
![]()
![]() et
et ![]() le sont) et vérifie manifestement :
le sont) et vérifie manifestement :
![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c}\pi_{1}\left(x\right)=x\\\text{et}\\\pi_{2}\left(x\right)=0_{E}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbad4f5e2c76656113aa5ebdb588c045_l3.png)
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
