
Certaines notions figurant au programme de première année de CPGE scientifique ou de licence de mathématiques s’avèrent moins faciles à assimiler que d’autres. Si l’on dressait une liste des 10 concepts qui posent le plus de difficultés aux étudiants, je peux dire par expérience que la notion d’image directe ou d’image réciproque y figurerait en bonne place.
L’objet de cette note est de contribuer à éclaircir un peu cette question et d’en montrer quelques unes des principales utilisations, à ce niveau.
Pré-requis :
- Notion d’application,
- Image d’un élément de l’ensemble de départ,
- Antécédents éventuels d’un élément de l’ensemble d’arrivée.
Pour réviser ces notions fondamentales, vous pouvez consultez les deux vidéos suivantes :
Correspondances, Fonctions, Applications – Partie 1
Correspondances, Fonctions, Applications – Partie 2
1 – Image directe : définition et premiers exemples
Considérons une application ![]() et une partie (= un sous-ensemble)
et une partie (= un sous-ensemble) ![]() de
de ![]() .
.
On appelle image directe de ![]() par
par ![]() l’ensemble :
l’ensemble :
![]()
![]() est donc l’ensemble des éléments de
est donc l’ensemble des éléments de ![]() qui sont l’image d’un élément de
qui sont l’image d’un élément de ![]() .
.
Reformulons …
![]() est l’ensemble des éléments de
est l’ensemble des éléments de ![]() possédant un antécédent dans
possédant un antécédent dans ![]() .
.
On peut écrire tout aussi bien :
![]()
Si ce qui précède n’est pas parfaitement limpide, les exemples qui suivent peuvent aider…
Exemple 1
On commence, c’est incontournable, par un exemple avec des « patates » 🙂
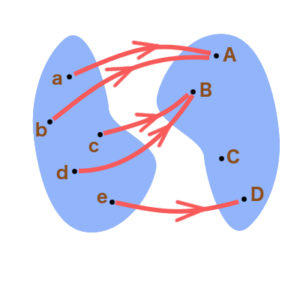
Si l’on note ![]() l’application représentée par le diagramme ci-contre et
l’application représentée par le diagramme ci-contre et ![]() ses ensembles de départ et d’arrivée, alors :
ses ensembles de départ et d’arrivée, alors :
![]()
![]()
![]()
Exemple 2
Pour ![]() , il est clair que
, il est clair que ![]() et que
et que ![]() est l’ensemble des entiers naturels impairs.
est l’ensemble des entiers naturels impairs.
Revenons au cas général et formulons trois remarques concernant une application ![]() .
.
- La condition
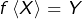 , lorsqu’elle est remplie, exprime la surjectivité de
, lorsqu’elle est remplie, exprime la surjectivité de  (tout élément de
(tout élément de  possède au moins un antécédent par
possède au moins un antécédent par  ).
). - Si
 , alors
, alors 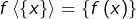 .
. - Enfin :
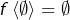 .
.
Continuons maintenant notre exploration, avec de nouveaux exemples…
Exemple 3
Pour ![]() , il est clair que
, il est clair que ![]() .
.
En fait : ![]() , mais pour quelle raison ? Et sauriez-vous déterminer
, mais pour quelle raison ? Et sauriez-vous déterminer ![]() ?
?
Réponses détaillées en ANNEXE, à la fin de l’article.
Exemple 4
Notons ![]() et considérons l’application
et considérons l’application
![]()
Alors ![]() est l’ensemble des entiers naturels pouvant s’écrire comme le produit de deux entiers strictement positifs, mais de manière non triviale (puisqu’aucun des deux facteurs ne peut valoir 1).
est l’ensemble des entiers naturels pouvant s’écrire comme le produit de deux entiers strictement positifs, mais de manière non triviale (puisqu’aucun des deux facteurs ne peut valoir 1).
On voit ainsi que ![]() est l’ensemble des nombres composés (autrement dit : non premiers) et supérieurs ou égaux à 4.
est l’ensemble des nombres composés (autrement dit : non premiers) et supérieurs ou égaux à 4.
2 – On marque une pause pour réfléchir à la notation

Vous vous demandez peut-être pourquoi je m’obstine à utiliser la notation ![]() alors qu’on trouve, dans pas mal de bouquins, la notation
alors qu’on trouve, dans pas mal de bouquins, la notation ![]() .
.
La raison est simple. Il faut à tout prix éviter la confusion entre :
- d’une part, l’image d’un élément
- d’autre part, l’image directe d’une partie
Aucun risque, me direz-vous : un élément et un partie, ce n’est pas la même chose ! Le contexte doit donc permettre de savoir de quoi on parle.
Il faut reconnaître que c’est souvent le cas en pratique… mais pas toujours !
Considérons l’ensemble :
![]()
Pas clair ? Allons au bout de cet exemple en définissant complètement ![]() :
:
![]()
![]()
J’espère vous avoir convaincu de la nécessité de noter différemment l’image d’un élément et l’image directe d’une partie.
3 – Deux exemples plus élaborés d’images directes
Exemple 5
Considérons l’application
![]()
![]()
![]()
Voyons maintenant ce qu’il en est de l’inclusion inverse…
Soit ![]() un couple de nombres réels vérifiant
un couple de nombres réels vérifiant ![]() .
.
Le discriminant de l’équation d’inconnue ![]() :
:
![]()
![]()
Si les « relations entre coefficients et racines » ne vous sont pas familières, vous pouvez simplement calculer :
![]()
![]()
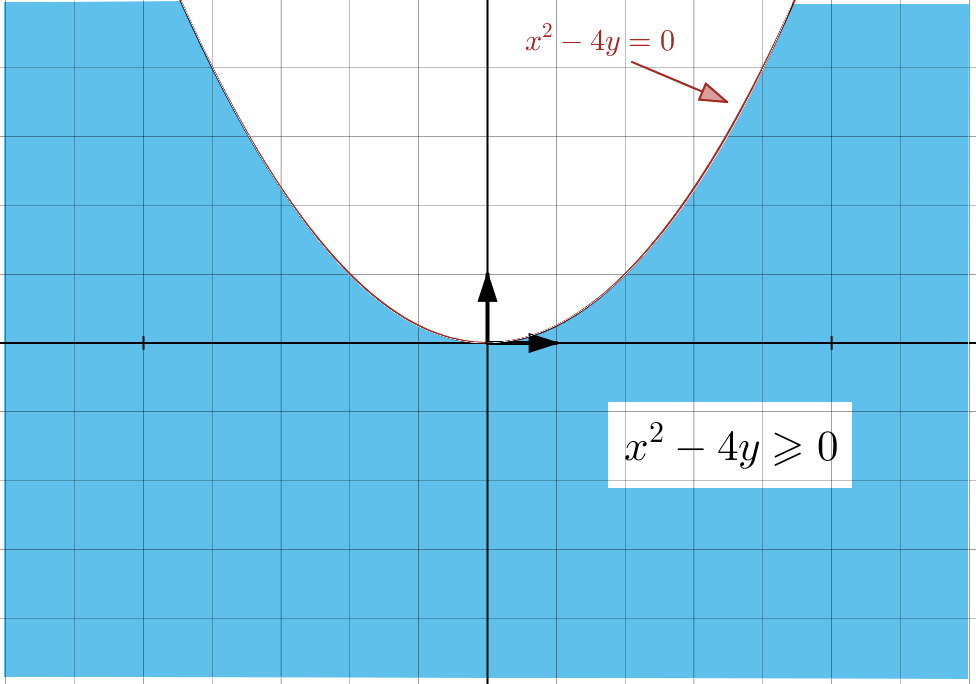
L’inclusion inverse est établie et finalement :
![]()
Au passage, ![]() est l’union de la parabole d’équation
est l’union de la parabole d’équation ![]() et de son « extérieur ». Dans la figure ci-dessous,
et de son « extérieur ». Dans la figure ci-dessous, ![]() est colorié en bleu :
est colorié en bleu :
Exemple 6
On sait depuis près de 23 siècles qu’il existe une infinité de nombres premiers. La preuve proposée par Euclide (Eléments, Livre IX, proposition 20) se résume à ceci :
Si ![]() sont des nombres premiers tous distincts, alors l’entier
sont des nombres premiers tous distincts, alors l’entier 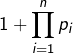 n’est divisible par aucun des
n’est divisible par aucun des ![]() pour
pour ![]() . Ses facteurs premiers se situent donc tous hors de l’ensemble
. Ses facteurs premiers se situent donc tous hors de l’ensemble ![]() .
.
Euclide prouve ainsi que l’ensemble ![]() ne saurait contenir tous les nombres premiers, d’où il déduit que l’ensemble
ne saurait contenir tous les nombres premiers, d’où il déduit que l’ensemble ![]() des nombres premiers est infini.
des nombres premiers est infini.
Considérons maintenant l’application ![]() définie par :
définie par :
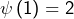
- Pour tout entier
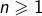 ,
, 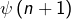 désigne le plus petit facteur premier de
désigne le plus petit facteur premier de![Rendered by QuickLaTeX.com \[Q_{n}=1+\prod_{i=1}^{n}\psi\left(i\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-27d20d4567ad04fcf04741b6e699d2ae_l3.png)
Par construction et d’après l’argument d’Euclide, les nombres ![]() sont tous premiers et sont deux à deux distincts. Calculons
sont tous premiers et sont deux à deux distincts. Calculons ![]() pour les petites valeurs de
pour les petites valeurs de ![]() :
:
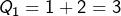 , donc
, donc 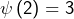
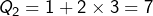 , donc
, donc 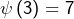
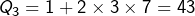 , donc
, donc 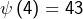
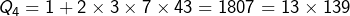 , donc
, donc 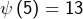
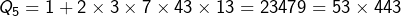 , donc
, donc 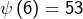
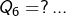
C’est à vous !! Réponse en ANNEXE, à la fin d’article.
La suite ![]() est connue sous le nom de suite de Euclide-Mullin (voir la note Recursive function theory (A modern look at a Euclidean idea) publiée en 1963 par A.A. Mullin dans le Bulletin of the American Mathematical Society).
est connue sous le nom de suite de Euclide-Mullin (voir la note Recursive function theory (A modern look at a Euclidean idea) publiée en 1963 par A.A. Mullin dans le Bulletin of the American Mathematical Society).
Il est bien évident que ![]() , mais la question de savoir si tout nombre premier est (ou non) un terme de cette suite demeure, depuis plus d’un demi-siècle, un problème ouvert !
, mais la question de savoir si tout nombre premier est (ou non) un terme de cette suite demeure, depuis plus d’un demi-siècle, un problème ouvert !
En d’autres termes, on ne connaît pas à ce jour l’image directe de ![]() par
par ![]() .
.
4 – Image réciproque : définition et premiers exemples
Considérons une application ![]() et une partie (= un sous-ensemble)
et une partie (= un sous-ensemble) ![]() de
de ![]() .
.
On appelle image réciproque de ![]() par
par ![]() l’ensemble :
l’ensemble :
![]()
« ![]() est l’ensemble des éléments
est l’ensemble des éléments ![]() de
de ![]() dont l’image par
dont l’image par ![]() appartient à
appartient à ![]() ».
».
Autrement dit : ![]() est l’ensemble des antécédents par
est l’ensemble des antécédents par ![]() des éléments de
des éléments de ![]() .
.
Exemple 7
On recommence avec les « patates »…

En notant à nouveau ![]() l’application représentée ci-contre et
l’application représentée ci-contre et ![]() ses ensembles de départ et d’arrivée :
ses ensembles de départ et d’arrivée :
![]()
![]()
![]() .
.
Exemple 8
Reprenons l’application ![]() de l’exemple
de l’exemple ![]() :
:
![]()
![]()
Or, d’une part :
![]()
![]()
Ainsi :
![]()
Cette relation est visualisée avec l’illustration suivante :
Exemple 9
Dans le cours de première année, on démontre que si ![]() ,
,![]() sont deux
sont deux ![]() -espaces vectoriels et si
-espaces vectoriels et si ![]() est linéaire, alors pour tout sous-espace vectoriel (sev)
est linéaire, alors pour tout sous-espace vectoriel (sev) ![]() de
de ![]() , l’image réciproque de
, l’image réciproque de ![]() par
par ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() . Vérifions ensemble cette propriété.
. Vérifions ensemble cette propriété.
On notera ![]() et
et ![]() les vecteurs nuls respectifs de
les vecteurs nuls respectifs de ![]() et de
et de ![]() .
.
Il s’agit de prouver d’une part que ![]() et d’autre part que
et d’autre part que ![]() est stable par combinaison linéaire.
est stable par combinaison linéaire.
Tout d’abord, comme ![]() est linéaire, on sait que
est linéaire, on sait que ![]() . Par ailleurs,
. Par ailleurs, ![]() étant un sev de
étant un sev de ![]() , on sait aussi que
, on sait aussi que ![]() . Il en résulte que :
. Il en résulte que :
![]()
Donnons-nous ensuite des vecteurs ![]() dans
dans ![]() et un scalaire
et un scalaire ![]() . Afin de prouver que
. Afin de prouver que ![]() , on calcule :
, on calcule :
![]()
Notons au passage qu’un cas particulier fondamental est celui où ![]() ; dans ce cas,
; dans ce cas, ![]() n’est autre que le noyau de
n’est autre que le noyau de ![]() . C’est ainsi que le noyau de toute application linéaire est un sev de son espace de départ.
. C’est ainsi que le noyau de toute application linéaire est un sev de son espace de départ.
5 – Une ambiguïté qui n’en est pas une
Etant donnée une bijection ![]() , la notation
, la notation ![]() est utilisée pour désigner sa bijection réciproque. Par conséquent, si
est utilisée pour désigner sa bijection réciproque. Par conséquent, si ![]() , une ambiguïté potentielle surgit lorsqu’on écrit
, une ambiguïté potentielle surgit lorsqu’on écrit ![]() .
.
S’agit-il :
- de l’image réciproque de
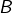 par
par  ?
? - ou bien de l’image directe de
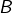 par
par 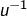 ?
?
Qu’on se rassure, cette ambiguïté n’est qu’apparente, car ces deux ensembles sont confondus. Prouvons cela en vérifiant soigneusement la double-inclusion.
Notons ![]() l’image réciproque de
l’image réciproque de ![]() par
par ![]() et
et ![]() l’image directe de
l’image directe de ![]() par
par ![]() :
:
- les éléments de
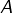 sont, par définition, les éléments
sont, par définition, les éléments  de
de  vérifiant
vérifiant 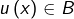 ,
, - les éléments de
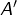 sont ceux de la forme
sont ceux de la forme 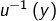 , pour
, pour 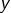 dans
dans 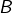 .
.
Si ![]() , alors
, alors ![]() . Ceci prouve que
. Ceci prouve que ![]()
Réciproquement, si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() , donc
, donc ![]() , ce qui prouve que
, ce qui prouve que ![]() , autrement dit que
, autrement dit que ![]() . Ceci prouve que
. Ceci prouve que ![]()
La double-inclusion est établie.
Ajoutons pour finir que si ![]() n’est pas bijective, alors le symbole
n’est pas bijective, alors le symbole ![]() n’est pas défini s’il est utilisé seul ! Mais on bien sûr écrire
n’est pas défini s’il est utilisé seul ! Mais on bien sûr écrire ![]() pour tout
pour tout ![]() .
.
6 – Quatre pattes ➡ Un mouton
En combinatoire, on utilise parfois le résultat suivant, connu sous le nom de « lemme des bergers ».
Etant donnés deux ensembles ![]() , on suppose que
, on suppose que ![]() est fini et qu’il existe une application
est fini et qu’il existe une application ![]() dont les fibres ont toutes le même cardinal
dont les fibres ont toutes le même cardinal ![]() .
.
Alors ![]() est fini et :
est fini et :
![]()
![]()
L’appellation « lemme des bergers » provient sans doute d’une plaisanterie : on imagine un berger voulant connaître le nombre de moutons de son troupeau… il lui suffit de compter les pattes puis de diviser par 4 l’entier obtenu !
L’illustration ci-dessous représente l’application qui va de l’ensemble des pattes vers celui des moutons et qui, à chaque patte, associe le mouton auquel elle appartient 🙂
Pour cette application, le lemme s’applique avec ![]() . On suppose évidemment que les moutons sont en bonne santé et qu’ils n’ont pas été manipulés génétiquement …
. On suppose évidemment que les moutons sont en bonne santé et qu’ils n’ont pas été manipulés génétiquement …
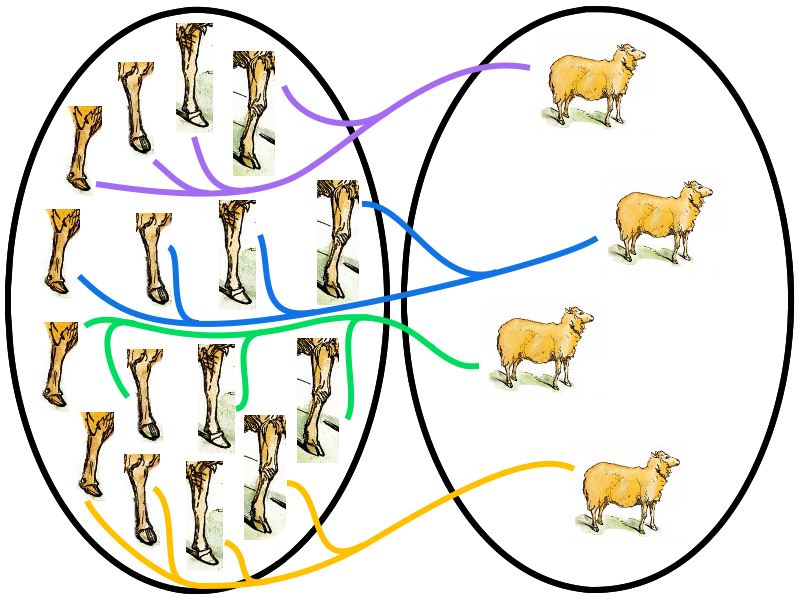
Citons un exemple d’utilisation du lemme des bergers :
Proposition
Si ![]() sont finis de cardinaux respectifs
sont finis de cardinaux respectifs ![]() et n avec
et n avec ![]() , alors il existe
, alors il existe ![]() injections de
injections de ![]() vers
vers ![]() .
.
On peut prouver cette proposition en raisonnant par récurrence sur le cardinal de ![]() (celui de
(celui de ![]() étant fixé). Pour
étant fixé). Pour ![]() , les
, les ![]() applications possibles sont évidemment toutes injectives, ce qui initialise la récurrence. Supposons la propriété établie au rang
applications possibles sont évidemment toutes injectives, ce qui initialise la récurrence. Supposons la propriété établie au rang ![]() , pour un certain
, pour un certain ![]() , et donnons-nous deux ensembles
, et donnons-nous deux ensembles ![]() de cardinaux respectifs
de cardinaux respectifs ![]() et
et ![]() .
.
Fixons un élément ![]() de
de ![]() et considérons l’application
et considérons l’application
![]()
Comme chaque injection de ![]() vers
vers ![]() peut être prolongée de
peut être prolongée de ![]() façons en une injection de
façons en une injection de ![]() vers
vers ![]() (en associant à
(en associant à ![]() l’un quelconque des
l’un quelconque des ![]() éléments encore disponibles), on voit que le lemme des bergers s’applique à
éléments encore disponibles), on voit que le lemme des bergers s’applique à ![]() et que :
et que :
![]()
7 – Image réciproque d’une image directe
Si ![]() et
et ![]() , alors
, alors ![]() . En effet, si
. En effet, si ![]() , alors
, alors ![]() (par définition de
(par définition de ![]() ) et donc
) et donc ![]() (par définition de
(par définition de ![]() avec
avec ![]() ).
).
Mais cette inclusion est en général stricte. Considérons en effet l’unique application ![]() et posons
et posons ![]() . Alors :
. Alors :
![]()
Cependant :
Proposition A
Si ![]() est injective, alors
est injective, alors ![]() , pour toute partie
, pour toute partie ![]() de
de ![]() .
.
En effet, étant donné ![]() , si
, si ![]() , alors
, alors ![]() ce qui signifie qu’il existe
ce qui signifie qu’il existe ![]() tel que
tel que ![]() . Comme
. Comme ![]() est injective, alors
est injective, alors ![]() et donc
et donc ![]() . Quant à l’autre inclusion, elle a été établie en toute généralité.
. Quant à l’autre inclusion, elle a été établie en toute généralité.
La réciproque de l’implication précédente est vraie :
Proposition réciproque
Si ![]() est telle que
est telle que ![]() pour toute partie
pour toute partie ![]() de
de ![]() , alors
, alors ![]() est injective.
est injective.
En effet, soient ![]() tels que
tels que ![]() . En choisissant
. En choisissant ![]() dans l’hypothèse, on constate que
dans l’hypothèse, on constate que ![]() . Or
. Or ![]() et donc
et donc ![]() .
.
8 – Image directe d’une image réciproque
Si ![]() et
et ![]() , alors
, alors ![]() . En effet, si
. En effet, si ![]() , alors (par définition de
, alors (par définition de ![]() avec
avec ![]() ) il existe
) il existe ![]() tel que
tel que ![]() et donc
et donc ![]() .
.
L’inclusion inverse n’est pas vraie en général, comme on le voit en considérant par exemple ![]() définie par
définie par ![]() et
et ![]() . On constate que :
. On constate que :
![]()
Proposition B
Si ![]() est surjective, alors
est surjective, alors ![]() pour toute partie
pour toute partie ![]() de
de ![]() .
.
En effet, étant donné ![]() , si
, si ![]() , alors il existe (par surjectivité de
, alors il existe (par surjectivité de ![]() ) un élément
) un élément ![]() tel que
tel que ![]() . Manifestement
. Manifestement ![]() et donc
et donc ![]() .
.
Réciproquement …
Proposition réciproque
Si ![]() est telle que
est telle que ![]() pour toute partie
pour toute partie ![]() de
de ![]() , alors
, alors ![]() est surjective.
est surjective.
En effet, soit ![]() . En choisissant
. En choisissant ![]() dans l’hypothèse, on voit que
dans l’hypothèse, on voit que ![]() . Ainsi
. Ainsi ![]() ; autrement dit,
; autrement dit, ![]() admet un antécédent par
admet un antécédent par ![]() .
.
9 – Image réciproque et topologie
Etant donnés un espace métrique ![]() (par exemple un espace vectoriel normé ou une partie d’un tel espace) ainsi qu’une partie
(par exemple un espace vectoriel normé ou une partie d’un tel espace) ainsi qu’une partie ![]() de
de ![]() , on a parfois besoin de prouver que
, on a parfois besoin de prouver que ![]() est un ouvert de
est un ouvert de ![]() . Pour cela, plusieurs méthodes existent. On peut…
. Pour cela, plusieurs méthodes existent. On peut…
- appliquer la définition d’un ouvert (c’est-à-dire vérifier, pour chaque
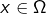 , l’existence d’une boule ouverte de centre
, l’existence d’une boule ouverte de centre  incluse dans
incluse dans  ),
), - prouver que le complémentaire dans
 de
de  est un fermé, en appliquant par exemple la caractérisation séquentielle des fermés (c’est-à-dire en vérifiant que pour toute suite convergente
est un fermé, en appliquant par exemple la caractérisation séquentielle des fermés (c’est-à-dire en vérifiant que pour toute suite convergente 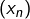 à termes dans le complémentaire
à termes dans le complémentaire  de
de  , la limite de cette suite appartient encore à
, la limite de cette suite appartient encore à 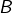 ),
), - trouver un espace métrique
 , un ouvert
, un ouvert 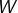 de
de  et une application continue
et une application continue 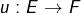 tels que
tels que 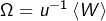 .
.
Cette troisième méthode repose donc sur le fait que « l’image réciproque d’un ouvert par une application continue est un ouvert ».
Par simple passage au complémentaire, on dispose de l’énoncé jumeau : « l’image réciproque d’un fermé par une application continue est un fermé ».
Ces deux énoncés s’avèrent très utiles en pratique. Donnons-en trois exemples d’utilisation.
Exemple 10 – A
Dans ![]() , l’hyperbole d’équation
, l’hyperbole d’équation ![]() est un fermé car c’est l’image réciproque du fermé
est un fermé car c’est l’image réciproque du fermé ![]() de
de ![]() par l’application
par l’application ![]() , qui est continue (puisque polynomiale).
, qui est continue (puisque polynomiale).
Plus généralement, toute courbe d’équation ![]() où
où ![]() est continue, est une partie fermée de
est continue, est une partie fermée de ![]() .
.
Ceci montre que les courbes ![]() d’équation polaire :
d’équation polaire :
![]()
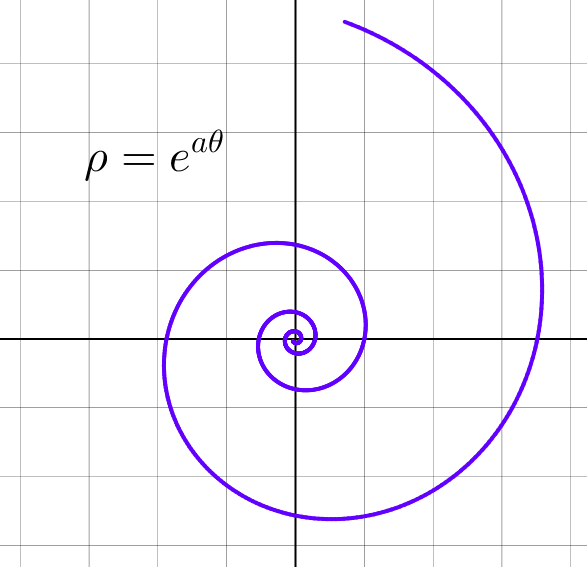
Exemple 10 – B
Dans ![]() , le groupe
, le groupe ![]() des matrices carrées inversibles est un ouvert puisque c’est l’image réciproque de l’ouvert
des matrices carrées inversibles est un ouvert puisque c’est l’image réciproque de l’ouvert ![]() de
de ![]() par l’application
par l’application ![]() qui est continue (puisque polynomiale, elle aussi).
qui est continue (puisque polynomiale, elle aussi).
On peut d’ailleurs montrer, plus précisément, que ![]() est un ouvert dense : toute matrice
est un ouvert dense : toute matrice ![]() est la limite d’une suite de matrices inversibles (il suffit de considérer la suite matricielle de terme général
est la limite d’une suite de matrices inversibles (il suffit de considérer la suite matricielle de terme général ![]() , pour
, pour ![]() ).
).
Exemple 10 – C
Dans ![]() , considérons deux parties
, considérons deux parties ![]() et
et ![]() , non vides et disjointes (on pourrait, sans rien changer d’essentiel, remplacer dans ce qui suit
, non vides et disjointes (on pourrait, sans rien changer d’essentiel, remplacer dans ce qui suit ![]() par un espace métrique quelconque).
par un espace métrique quelconque).
Une question classique consiste se demander si l’on peut les séparer, c’est-à-dire s’il existe des ouverts ![]() et
et ![]() disjoints tels que
disjoints tels que ![]() et
et ![]() . La réponse est en général négative, mais si
. La réponse est en général négative, mais si ![]() et
et ![]() sont fermés, elle devient affirmative !
sont fermés, elle devient affirmative !
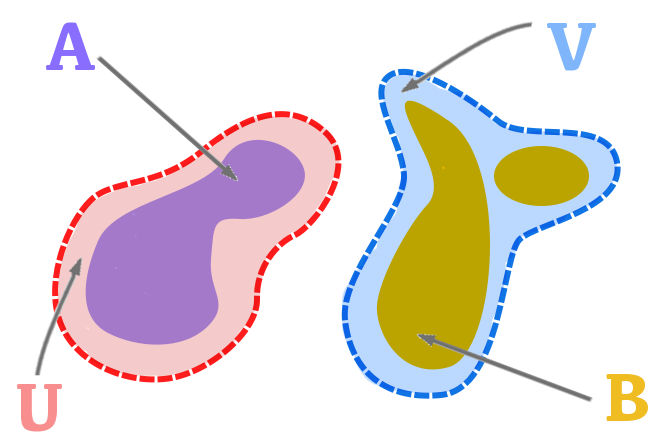
En effet, notons :
➡ ![]() la norme euclidienne d’un vecteur
la norme euclidienne d’un vecteur ![]() .
.
➡ ![]() la distance d’un vecteur
la distance d’un vecteur ![]() à une partie
à une partie ![]() , définie par :
, définie par :
![]()
Pour tout ![]() , l’application
, l’application ![]() est continue car
est continue car ![]() lipschitzienne.
lipschitzienne.
On sait par ailleurs que ![]() si, et seulement si,
si, et seulement si, ![]() (l’adhérence de
(l’adhérence de ![]() ). En particulier, si
). En particulier, si ![]() est fermé dans
est fermé dans ![]() , alors :
, alors : ![]() .
.
Sauriez-vous établir ces points ? Solution en ANNEXE !
![]() l’application définie sur
l’application définie sur ![]() par :
par :
![]()
Comme ![]() est continue (différence de deux applications continues), alors les ensembles
est continue (différence de deux applications continues), alors les ensembles
![]()
![]()
On voit de même que ![]() . On peut donc toujours séparer, dans
. On peut donc toujours séparer, dans ![]() comme dans n’importe quel espace métrique, deux fermés non vides et disjoints.
comme dans n’importe quel espace métrique, deux fermés non vides et disjoints.
Terminons en remarquant que l’image directe d’un ouvert par une application continue n’est pas, en général, un ouvert de l’espace d’arrivée. Par exemple, l’application
![]()
10 – Annexe
Section 1 – Exemple 3
- C’est une conséquence du théorème des valeurs intermédiaires. Considérons en effet un réel
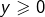 . Comme
. Comme 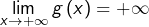 , il existe
, il existe 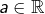 tel que
tel que 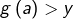 . Comme
. Comme 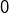 et
et 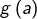 sont atteints par
sont atteints par 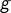 , alors tout réel compris entre
, alors tout réel compris entre 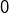 et
et 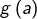 est aussi atteint : c’est en particulier le cas de
est aussi atteint : c’est en particulier le cas de 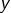 . Ceci prouve que
. Ceci prouve que 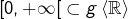 . L’inclusion réciproque étant évidente (le carré de tout nombre réel est positif ou nul), on a l’égalité.
. L’inclusion réciproque étant évidente (le carré de tout nombre réel est positif ou nul), on a l’égalité. - Les variations de
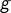 (décroissance sur
(décroissance sur ![Rendered by QuickLaTeX.com \left]-\infty,0\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2a8d889c1500417239792c75ec84b984_l3.png) et croissance sur
et croissance sur 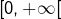 ) et sa continuité montrent que
) et sa continuité montrent que
et que![Rendered by QuickLaTeX.com \[g\left\langle \left[-1,0\right]\right\rangle =\left[g\left(0\right),g\left(-1\right)\right]=\left[0,1\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-33dca335d61fa1d0106df1b183efcd2d_l3.png)
Par conséquent :![Rendered by QuickLaTeX.com \[g\left\langle \left[0,2\right]\right\rangle =\left[g\left(0\right),g\left(2\right)\right]=\left[0,4\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36c0f445aa11d83d13d5465f5cc6273c_l3.png)
![Rendered by QuickLaTeX.com \[g\left\langle \left[-1,2\right]\right\rangle =g\left\langle \left[-1,0\right]\cup\left[0,2\right]\right\rangle =g\left\langle \left[-1,0\right]\right\rangle \cup g\left\langle \left[0,2\right]\right\rangle =\left[0,4\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3299a0b846c08dd4c316baa0491967fe_l3.png)
Section 3 – Exemple 6
Après ![]()
![]()
![]()
![]()
![]() et
et ![]() le terme suivant est
le terme suivant est ![]() . En effet :
. En effet :
![]()
![]()
Section 9 – Point numéro 3
Deux propriétés de la distance à une partie
- Soient
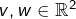 . Pour tout
. Pour tout 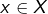 :
:
et donc :![Rendered by QuickLaTeX.com \[d\left(v,X\right)\leqslant\left\Vert v-x\right\Vert =\left\Vert v-w+w-x\right\Vert \leqslant\left\Vert v-w\right\Vert +\left\Vert w-x\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-87301a902722626655a1930275e7e437_l3.png)
En passant à la borne inférieure :![Rendered by QuickLaTeX.com \[d\left(v,X\right)-\left\Vert v-w\right\Vert \leqslant\left\Vert w-x\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-520eb42b519375ff1531b0c2b3d4e42b_l3.png)
Autrement dit :![Rendered by QuickLaTeX.com \[d\left(v,X\right)-\left\Vert v-w\right\Vert \leqslant d\left(w,X\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ac2d6a49b4577a1356a9234ae501c3a3_l3.png)
Mais![Rendered by QuickLaTeX.com \[d\left(v,X\right)-d\left(w,X\right)\leqslant\left\Vert v-w\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cc4e93c8365769fdf09728a9453e7e47_l3.png)
 et
et 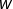 jouent ici des rôles symétriques ! On a donc aussi :
jouent ici des rôles symétriques ! On a donc aussi :
d’où finalement :![Rendered by QuickLaTeX.com \[d\left(w,X\right)-d\left(v,X\right)\leqslant\left\Vert v-w\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-06ff007c383143ce6f8ca87522323fd3_l3.png)
Ceci montre que l’application![Rendered by QuickLaTeX.com \[\boxed{\left|d\left(v,X\right)-d\left(w,X\right)\right|\leqslant\left\Vert v-w\right\Vert}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64271c0651f114844244652b64a697b8_l3.png)
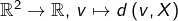 est
est 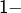 lipschitzienne, donc continue.
lipschitzienne, donc continue. - Si
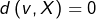 alors, d’après la caractérisation séquentielle d’une borne inférieure, il existe une suite
alors, d’après la caractérisation séquentielle d’une borne inférieure, il existe une suite 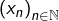 d’éléments de
d’éléments de  telle que
telle que 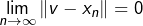 . On voit ainsi que
. On voit ainsi que  est adhérent à X. Réciproquement, si
est adhérent à X. Réciproquement, si  est adhérent à
est adhérent à  , alors une telle suite existe et en passant à la limite dans l’encadrement
, alors une telle suite existe et en passant à la limite dans l’encadrement 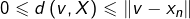 , on obtient
, on obtient 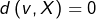 .
.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonsoir Monsieur,
Merci pour cet article !
On comprend très bien sans, mais sauf erreur de ma part, il manque quelques accolades ensemblistes dans :
– l’exemple 8 de la section 4 ;
– les trois dernières lignes qui précédent la section 8 ;
– les deux dernières lignes qui précédent la section 9.
Bien à vous
C’est corrigé ! Merci, une fois encore, pour votre lecture millimétrique 🙂