Neuf énoncés d’exercices sur les suites numériques (fiche 02).
Que peut-on dire d’une suite réelle croissante et périodique ?
Etant donné ![Rendered by QuickLaTeX.com \theta\in\left[0,1\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-0dc364a97b18c3a083fd321832eb47d2_l3.png) on définit une suite
on définit une suite 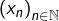 en posant :
en posant :
![Rendered by QuickLaTeX.com \[ x_{0}=\sin^{2}\left(\theta\right)\qquad\text{et}\qquad\forall n\in\mathbb{N},\thinspace x_{n+1}=4x_{n}\left(1-x_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e15f0f380b272a3c00bc0faa1a56db6d_l3.png)
Calculer
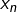
pour tout
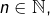
en fonction de

et de
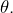
Soit 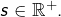 Etudier la nature (convergence ou divergence) de la suite définie par :
Etudier la nature (convergence ou divergence) de la suite définie par :
![Rendered by QuickLaTeX.com \[u_{0}=s\qquad\text{et}\qquad\forall n\in\mathbb{N},\thinspace u_{n+1}=u_{n}^{2}+\frac{1}{4}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c0faa4c15f644ee965da7ac0f554c4bb_l3.png)
On se donne deux réels 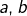 tels que
tels que 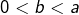 .
.
On définit deux suites réelles 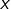 et
et 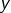 en posant
en posant 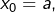
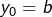 et :
et :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace\left\{ \begin{array}{ccc}x_{n+1} & = & \dfrac{x_{n}+y_{n}}{2}\\\\y_{n+1} & = & \dfrac{2x_{n}y_{n}}{x_{n}+y_{n}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36ea3497acf8b8c04900af07773e2461_l3.png)
Montrer que les suites
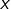
et
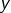
convergent vers une limite commune
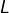
.
Exprimer 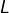 en fonction de
en fonction de  et de
et de 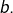
Etant donné un réel 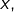 on définit un couple
on définit un couple 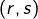 de suites en posant, pour tout
de suites en posant, pour tout 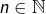 :
:
![Rendered by QuickLaTeX.com \[r_{n}=10^{-n}\left\lfloor 10^{n}x\right\rfloor \qquad\text{et}\qquad s_{n}=10^{-n}\left\lceil 10^{n}x\right\rceil\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d81140461e296ce6ce4be142e840c95b_l3.png)
Montrer que

et

convergent vers une même limite.
On rappelle que, si 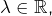 on note
on note 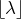 (resp.
(resp. 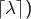 la partie entière par défaut (resp. par excès) de
la partie entière par défaut (resp. par excès) de 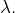
Si ces notations ne sont pas claires, se reporter au lexique.
Soit 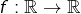 une application continue et soit
une application continue et soit 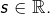
On définit une suite 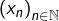 en posant :
en posant :
![Rendered by QuickLaTeX.com \[x_{0}=s\qquad\text{et}\qquad\forall n\in\mathbb{N},\thinspace x_{n+1}=f\left(x_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f3797dfb61544b36a2c63bfecc7da00c_l3.png)
On suppose cette suite non monotone. Montrer que

possède au moins un point fixe.
Mêmes notations qu’à l’exercice précédent, à ceci près que ![Rendered by QuickLaTeX.com f:[0,1]\to[0,1]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c78ae09d9aca601ddeb956d6f9779c5d_l3.png) .
.
Soit 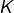 l’ensemble des valeurs d’adhérence de la suite
l’ensemble des valeurs d’adhérence de la suite 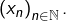 Montrer que :
Montrer que :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}d\left(x_{n},K\right)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0d544e0115aabd0c250c02f67c591e4a_l3.png)
On rappelle que, si 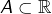 est non vide et si
est non vide et si 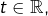 alors par définition :
alors par définition :
![Rendered by QuickLaTeX.com \[d\left(t,A\right)=\inf\left\{ \left|t-a\right|;\thinspace a\in A\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-592210f5ad5f5962be8e9ae43b2e8e1b_l3.png)
C’est la distance de
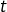
à
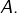
Si nécessaire, consulter
le lexique.
Déterminer l’ensemble des valeurs d’adhérence de la suite de terme général :
![Rendered by QuickLaTeX.com \[u_{n}=\sqrt{n}-\left\lfloor \sqrt{n}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bf77789cfd9ef95dd235ab7c0a9c31b0_l3.png)
Montrer que de toute suite réelle, on peut extraire une sous-suite monotone. En déduire une preuve courte du théorème de Bolzano-Weierstrass (de toute suite réelle bornée, on peut extraire une sous-suite convergente).


![]() on définit une suite
on définit une suite ![]() en posant :
en posant : ![]()

![]()

![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace\left\{ \begin{array}{ccc}x_{n+1} & = & \dfrac{x_{n}+y_{n}}{2}\\\\y_{n+1} & = & \dfrac{2x_{n}y_{n}}{x_{n}+y_{n}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36ea3497acf8b8c04900af07773e2461_l3.png)

![]()

![]()

![]()
![]()

![]()



![]() on définit une suite
on définit une suite ![]() en posant :
en posant : ![]()

![]()

![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace\left\{ \begin{array}{ccc}x_{n+1} & = & \dfrac{x_{n}+y_{n}}{2}\\\\y_{n+1} & = & \dfrac{2x_{n}y_{n}}{x_{n}+y_{n}}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36ea3497acf8b8c04900af07773e2461_l3.png)

![]()

![]()

![]()
![]()

![]()
