Lettre P
PARTIE (d’un ensemble)
Les parties d’un ensemble ![]() , appelées aussi sous-ensembles de
, appelées aussi sous-ensembles de ![]() , sont les ensembles inclus dans
, sont les ensembles inclus dans ![]() .
.
Par exemple, les parties de ![]() sont
sont ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
On note ![]() l’ensemble des parties de
l’ensemble des parties de ![]() .
.
On peut montrer que si ![]() est fini, alors
est fini, alors ![]() aussi et :
aussi et :
![]()
Quel que soit l’ensemble ![]() , il n’existe aucune surjection (et en particulier aucune bijection) de
, il n’existe aucune surjection (et en particulier aucune bijection) de ![]() vers
vers ![]() .
.
PARTIE ENTIERE, PARTIE FRACTIONNAIRE
Etant donné un réel ![]() on note
on note ![]() la partie entière par défaut de
la partie entière par défaut de ![]()
C’est le plus grand entier ![]() vérifiant
vérifiant ![]() Autrement dit :
Autrement dit :
![]()
Par exemple :
![]()
Quant à la différence ![]() , elle est appelée partie fractionnaire de
, elle est appelée partie fractionnaire de ![]() et notée
et notée ![]() (si toutefois le contexte permet d’éviter toute confusion avec un singleton).
(si toutefois le contexte permet d’éviter toute confusion avec un singleton).
On définit de manière analogue la partie entière par excès de ![]() notée
notée ![]() C’est le plus petit entier
C’est le plus petit entier ![]() vérifiant
vérifiant ![]() Ainsi :
Ainsi :
![]()
![]()
Par défaut, l’expression « partie entière » désigne la partie entière par défaut 🙂
Remarque
Si ![]() est entier, il est clair que :
est entier, il est clair que :
![]()
![]()
Graphe de la fonction ![]() :
:
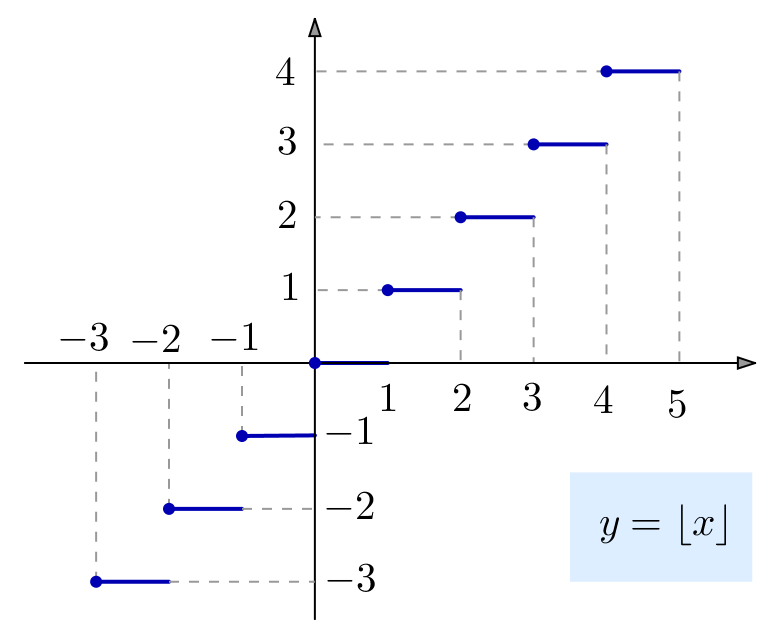
La relation ![]() exprime l’invariance du graphe de
exprime l’invariance du graphe de ![]() par la translation de vecteur
par la translation de vecteur ![]() Il revient au même de dire que la fonction partie fractionnaire est 1-périodique.
Il revient au même de dire que la fonction partie fractionnaire est 1-périodique.
Une jolie formule (parmi d’autres) faisant intervenir des parties entières :
Théorème
(formule de Legendre)
Pour tout nombre premier ![]() et tout entier
et tout entier ![]() la valuation
la valuation ![]() adique de
adique de ![]() est :
est :
![Rendered by QuickLaTeX.com \[v_{p}\left(n!\right)=\sum_{j=1}^{\infty}\left\lfloor \frac{n}{p^{j}}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c0aae871afcd98ed8fece76b5aca1517_l3.png)
En fait, cette somme est finie, car ![]() dès que
dès que ![]() est assez grand.
est assez grand.
Concernant la formule de Legendre, on pourra consulter cet article
PARTITION (d’un ensemble)
Etant donné une ensemble non vide ![]() , une partition de
, une partition de ![]() est un ensemble
est un ensemble ![]() de parties de
de parties de ![]() telles que :
telles que :
- chaque
 est non vide
est non vide - les
 sont deux à deux disjoints
sont deux à deux disjoints  est l’union des
est l’union des 
Noter que l’ensemble d’indices ![]() peut éventuellement être infini.
peut éventuellement être infini.
Exemples
- Si
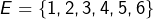 , alors en posant :
, alors en posant :
l’ensemble![Rendered by QuickLaTeX.com \[A_1=\{1,2\}\quad A_2=\{3\}\quad A_3=\{4,5,6\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4342ab2ea8eb8a9126ea9a63bc7a6177_l3.png)
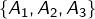 est une partition de
est une partition de  .
. - Etant donné un entier
 , si l’on note pour tout
, si l’on note pour tout 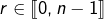 :
:
alors les![Rendered by QuickLaTeX.com \[A_r=r+n\mathbb{Z}=\{r+nk;\,k\in\mathbb{Z}\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-361244a0312cda07b49e472a6c4fe1a1_l3.png)
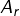 forment une partition de
forment une partition de 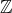 .
. - Si l’on note
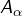 l’ensemble des applications de
l’ensemble des applications de  dans
dans  qui prennent la valeur
qui prennent la valeur 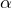 en 0, alors l’ensemble
en 0, alors l’ensemble 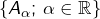 est une partition de
est une partition de 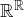 .
.
Etant donné un groupe ![]() , l’ensemble de ses sous-groupes ne forme pas une partition de
, l’ensemble de ses sous-groupes ne forme pas une partition de ![]() . En effet, les sous-groupes de
. En effet, les sous-groupes de ![]() sont tous non vide et leur union est
sont tous non vide et leur union est ![]() , mais ils ne sont pas deux à deux disjoints (puisqu’ils contiennent tous l’élément neutre).
, mais ils ne sont pas deux à deux disjoints (puisqu’ils contiennent tous l’élément neutre).
Si ![]() est un ensemble fini de cardinal
est un ensemble fini de cardinal ![]() , alors le nombre de partitions de
, alors le nombre de partitions de ![]() est le n-ème nombre de Bell, noté
est le n-ème nombre de Bell, noté ![]() . Voir cet article.
. Voir cet article.
PERMUTATION
Etant donné un ensemble non vide ![]() une permutation de
une permutation de ![]() est une bijection dans
est une bijection dans ![]() dans lui-même.
dans lui-même.
L’ensemble des permutations de ![]() est noté
est noté ![]() (la lettre
(la lettre ![]() est le S de l’alphabet fraktur, un type d’écriture gothique). Comme la composée de deux bijections est une bijection, la loi
est le S de l’alphabet fraktur, un type d’écriture gothique). Comme la composée de deux bijections est une bijection, la loi ![]() est une opération dans l’ensemble
est une opération dans l’ensemble ![]() Elle lui confère une structure de groupe. Ce groupe est non abélien dès que
Elle lui confère une structure de groupe. Ce groupe est non abélien dès que ![]() plus précisément, son centre est réduit à
plus précisément, son centre est réduit à ![]() Les groupes
Les groupes ![]() et
et ![]() sont isomorphes si, et seulement si,
sont isomorphes si, et seulement si, ![]() et
et ![]() sont équipotents.
sont équipotents.
On peut montrer que tout groupe ![]() est isomorphe à un sous-groupe de
est isomorphe à un sous-groupe de ![]() (théorème de Cayley), ce qui montre le caractère universel des groupes de permutations.
(théorème de Cayley), ce qui montre le caractère universel des groupes de permutations.
Parmi les éléments de ![]() on distingue les cycles. Etant donnés
on distingue les cycles. Etant donnés ![]() des éléments distincts de
des éléments distincts de ![]() la bijection
la bijection ![]() définie par :
définie par :
![]()
![]()
Un 2-cycle (ou transposition) échange deux éléments et laisse les autres fixes.
Si ![]() on note
on note ![]() pour
pour ![]() Le groupe
Le groupe ![]() est appelé
est appelé ![]() ème groupe symétrique. C’est un groupe de cardinal
ème groupe symétrique. C’est un groupe de cardinal ![]() (la factorielle de
(la factorielle de ![]() engendré par les transpositions (plus précisément, les
engendré par les transpositions (plus précisément, les ![]() transpositions
transpositions ![]() pour
pour ![]() forment une partie génératrice de
forment une partie génératrice de ![]()
Exemple
Les ![]() éléments de
éléments de ![]() sont les suivants :
sont les suivants :
![Rendered by QuickLaTeX.com \[\begin{array}{ccccc}\left(\begin{array}{ccc}1 & 2 & 3\\1 & 2 & 3\end{array}\right) & & \left(\begin{array}{ccc}1 & 2 & 3\\1 & 3 & 2\end{array}\right) & & \left(\begin{array}{ccc}1 & 2 & 3\\3 & 2 & 1\end{array}\right)\\\\\left(\begin{array}{ccc}1 & 2 & 3\\2 & 1 & 3\end{array}\right) & & \left(\begin{array}{ccc}1 & 2 & 3\\2 & 3 & 1\end{array}\right) & & \left(\begin{array}{ccc}1 & 2 & 3\\3 & 1 & 2\end{array}\right)\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6dd90820d249fa07c869dfd23c8d29eb_l3.png)
La matrice
![]()
Ces six éléments sont donc :
- l’identité de
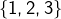 : c’est l’élément neutre du groupe
: c’est l’élément neutre du groupe - les trois transpositions : celle qui échange 2 et 3, celle qui échange 1 et 3, celle qui échange 1 et 2.
- les deux permutations circulaires
PION (formule du)
Etant donnés des entiers ![]() tels que
tels que ![]() , l’égalité :
, l’égalité :
![]()
La formule du pion se généralise sous la forme suivante :
![]()
PREMIER (nombre)
Un nombre entier ![]() est dit premier lorsqu’il possède exactement deux diviseurs (positifs), à savoir : 1 et
est dit premier lorsqu’il possède exactement deux diviseurs (positifs), à savoir : 1 et ![]() lui-même.
lui-même.
Ainsi, 15 n’est pas premier puisque cet entier n’est pas seulement divisible par 1 et 15 (mais aussi par 3 et 5).

Ne pas confondre avec la notion de nombres premiers entre eux.
L’ensemble des nombres premiers, noté ![]() , est infini. Ses huit plus petits éléments sont :
, est infini. Ses huit plus petits éléments sont :
![]()
On peut montrer que tout entier ![]() se décompose, de manière unique, en produit de facteurs premiers, sous la forme :
se décompose, de manière unique, en produit de facteurs premiers, sous la forme :
![Rendered by QuickLaTeX.com \[n=\prod_{i=1}^rp_i^{\alpha_i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-528e3aab8a901badb609d4b021af1a3f_l3.png)
Ce résultat constitue le théorème fondamental de l’arithmétique.
Exemples
![]()
![]()
Plusieurs questions, simple à formuler, restent à ce jour sans réponse :
- est-il vrai que tout nombre pair supérieur ou égal à 4 est la somme de deux nombres premiers ?
- est-il vrai qu’il existe une infinité de nombres premiers p tels que p+2 soit aussi premier ?
- existe-t-il une infinité de nombres premiers de la forme
 ?
? - existe-t-il un entier
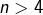 tel que
tel que 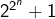 soit premier ?
soit premier ?
Pour en savoir plus sur les nombres premiers, on pourra consulter cet article ou cette vidéo.
PRODUIT CARTÉSIEN
Etant donnés deux objets mathématiques quelconques ![]() et
et ![]() , on note
, on note ![]() le couple qu’ils forment (dans cet ordre).
le couple qu’ils forment (dans cet ordre).
Une façon de rattacher cette notion à celle d’ensemble est de considérer que ![]() désigne l’ensemble
désigne l’ensemble ![]() , mais cet subtilité n’est pas importante en pratique … ce qui compte, c’est de se rappeler qu’un couple est ordonné. Ainsi, les couples d’entiers
, mais cet subtilité n’est pas importante en pratique … ce qui compte, c’est de se rappeler qu’un couple est ordonné. Ainsi, les couples d’entiers ![]() et
et ![]() sont distincts.
sont distincts.
Par contraste, les ensembles ![]() et
et ![]() sont identiques.
sont identiques.
Etant donné un couple ![]() , on dit que
, on dit que ![]() (resp.
(resp. ![]() ) est la première composante (resp. la seconde composante) de
) est la première composante (resp. la seconde composante) de ![]() .
.
Maintenant, si ![]() et
et ![]() sont deux ensembles quelconques, on note
sont deux ensembles quelconques, on note ![]() l’ensemble des couples
l’ensemble des couples ![]() pour lesquels
pour lesquels ![]() et
et ![]() . Cet ensemble est appelé produit cartésien de
. Cet ensemble est appelé produit cartésien de ![]() par
par ![]() .
.
Par exemple, si ![]() et
et ![]() , alors :
, alors :
![]()
On généralise la notion de couple en celle de ![]() -uplet (ou : liste de longueur
-uplet (ou : liste de longueur ![]() ), avec
), avec ![]() un entier plus grand que 1.
un entier plus grand que 1.
Si ![]() sont des ensembles quelconques, leur produit cartésien (dans cet ordre) est défini comme l’ensemble des
sont des ensembles quelconques, leur produit cartésien (dans cet ordre) est défini comme l’ensemble des ![]() -uplets
-uplets ![]() , avec
, avec ![]() , … etc …,
, … etc …, ![]() .
.
Cet ensemble est noté ![]() , ou bien de manière abrégée :
, ou bien de manière abrégée : ![]() .
.
PROPRE (valeur, vecteur)
Soient un ![]() espace vectoriel
espace vectoriel ![]() un endomorphisme
un endomorphisme ![]() et
et ![]() un scalaire.
un scalaire.
Ce scalaire est appelé une valeur propre de ![]() lorsque :
lorsque :
![]()
Un tel ![]() est appelé un vecteur propre pour
est appelé un vecteur propre pour ![]() associé à la valeur propre
associé à la valeur propre ![]()
L’ensemble des valeurs propres de ![]() est le spectre de
est le spectre de ![]() noté
noté ![]() C’est une partie de
C’est une partie de ![]()
Si ![]() est de dimension finie, alors
est de dimension finie, alors ![]() est fini et
est fini et ![]()
En revanche, si ![]() le spectre d’un endomorphisme peut être infini : voir l’exemple n° 4 ci-dessous ou encore cette vidéo.
le spectre d’un endomorphisme peut être infini : voir l’exemple n° 4 ci-dessous ou encore cette vidéo.
Exemples
- Si
 est une homothétie, c’est-à-dire
est une homothétie, c’est-à-dire 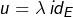 pour un certain
pour un certain 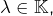 alors
alors 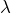 est l’unique valeur propre de
est l’unique valeur propre de  et tout vecteur non nul est propre pour
et tout vecteur non nul est propre pour 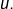
- Si
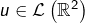 est canoniquement associé à
est canoniquement associé à ![Rendered by QuickLaTeX.com \left[\begin{array}{cc}0 & -1\\1 & 0\end{array}\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-87efa4e05a11b610626a7bd9fb0d783f_l3.png) alors
alors  ne possède aucune valeur propre (et il n’existe donc aucun vecteur propre pour
ne possède aucune valeur propre (et il n’existe donc aucun vecteur propre pour 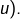 Ceci est géométriquement évident, puisque
Ceci est géométriquement évident, puisque  est la rotation de mesure
est la rotation de mesure 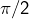 : on voit mal comment un vecteur non nul pourrait être colinéaire à son image …
: on voit mal comment un vecteur non nul pourrait être colinéaire à son image … - Si
 est de dimension finie et si
est de dimension finie et si 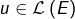 est nilpotent, c’est-à-dire s’il existe
est nilpotent, c’est-à-dire s’il existe 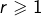 tel que
tel que 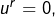 alors
alors 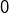 est la seule valeur propre de
est la seule valeur propre de 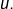
- Si
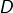 désigne l’endomorphisme de dérivation de
désigne l’endomorphisme de dérivation de 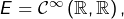 alors tout réel
alors tout réel 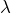 est valeur propre de
est valeur propre de 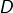 puisque l’application
puisque l’application 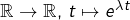 (qui n’est pas l’application nulle) appartient à
(qui n’est pas l’application nulle) appartient à  et vérifie
et vérifie 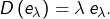
Si ![]() alors l’ensemble
alors l’ensemble ![]() est le sous-espace propre (sep) pour
est le sous-espace propre (sep) pour ![]() associé à la valeur propre
associé à la valeur propre ![]() C’est donc la partie de
C’est donc la partie de ![]() formée du vecteur nul et des vecteurs propres pour
formée du vecteur nul et des vecteurs propres pour ![]() associés à la valeur propre
associés à la valeur propre ![]()
On peut montrer que, si ![]() est de dimension finie, alors la somme des sep pour
est de dimension finie, alors la somme des sep pour ![]() est directe. Lorsque cette somme directe coïncide avec
est directe. Lorsque cette somme directe coïncide avec ![]() l’endomorphisme
l’endomorphisme ![]() est dit diagonalisable.
est dit diagonalisable.

