Soit ![]() un entier tel que
un entier tel que ![]() et soient
et soient ![]() et
et ![]() des réels.
des réels.
Vérifier que :
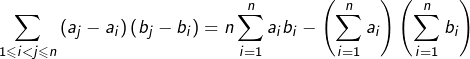
En déduire que si ![]() sont croissantes alors :
sont croissantes alors :
![]()
Une solution est disponible ici
Soit ![]() un entier tel que
un entier tel que ![]() et soient
et soient ![]() et
et ![]() des réels.
des réels.
Vérifier que :
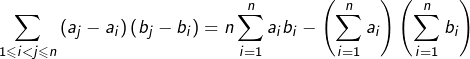
En déduire que si ![]() sont croissantes alors :
sont croissantes alors :
![]()
Une solution est disponible ici