Solutions détaillées de neuf exercices sur les suites numériques (fiche 02).
Cliquer ici pour accéder aux énoncés.


Soit ![]() une suite réelle croissante et
une suite réelle croissante et ![]() périodique (avec
périodique (avec ![]() et soient
et soient ![]() tels que
tels que ![]()
D’une part : ![]() D’autre part, il existe
D’autre part, il existe ![]() tel que
tel que ![]() et donc
et donc ![]()
Ainsi : ![]() En conclusion, toute suite réelle croissante et périodique est nécessairement constante (et même conclusion pour une suite décroissante et périodique : il suffit d’appliquer ce qui précède à la suite opposée).
En conclusion, toute suite réelle croissante et périodique est nécessairement constante (et même conclusion pour une suite décroissante et périodique : il suffit d’appliquer ce qui précède à la suite opposée).

On montre par récurrence que, pour tout ![]() :
:
![]()
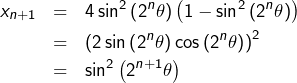
Si cette suite converge, sa limite ![]() doit vérifier
doit vérifier ![]() et donc
et donc ![]() Pour tout
Pour tout ![]() :
:
![]()
- Si
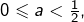 la suite
la suite  est majorée par
est majorée par 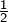 (récurrence immédiate) donc converge (vers
(récurrence immédiate) donc converge (vers 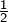 d’après ce qui a été dit plus haut).
d’après ce qui a été dit plus haut). - Si
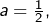 la suite
la suite  est constante !
est constante ! - Enfin, si
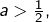 la suite
la suite  n’est pas majorée, car sinon elle convergerait et sa limite
n’est pas majorée, car sinon elle convergerait et sa limite 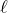 vérifierait
vérifierait 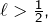 ce qui n’est pas possible. Elle est ainsi croissante et non majorée, donc diverge vers
ce qui n’est pas possible. Elle est ainsi croissante et non majorée, donc diverge vers 
Illustration dynamique
On voit ci-dessous les graphes de ![]() et de
et de ![]() , ainsi qu’une ligne polygonale montrant le calcul des premiers termes de la suite
, ainsi qu’une ligne polygonale montrant le calcul des premiers termes de la suite ![]() . En déplaçant le curseur latéralement tout en pressant la touche SHIFT, on fait varier la valeur de
. En déplaçant le curseur latéralement tout en pressant la touche SHIFT, on fait varier la valeur de ![]() , c’est-à-dire de
, c’est-à-dire de ![]() .
.

Tout d’abord, les deux suites sont bien définies et à termes strictement positifs. Ensuite, on observe que ![]() et que, pour tout
et que, pour tout ![]() :
:
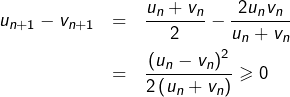
![]()
![]()
![]()
![]()
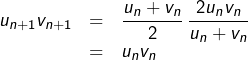
![]()
![]()
Remarque
Il est intéressant de noter que, pour tout ![]()
![]() (resp.
(resp. ![]() est la moyenne arithmétique (resp. harmonique) de
est la moyenne arithmétique (resp. harmonique) de ![]() et
et ![]() Les deux suites convergent vers une limite commune : la moyenne géométrique des deux termes initiaux.
Les deux suites convergent vers une limite commune : la moyenne géométrique des deux termes initiaux.
Pour préciser ces histoires de moyennes, on pourra consulter le lexique

Vérifions que la suite ![]() est croissante et converge vers
est croissante et converge vers ![]() et que la suite
et que la suite ![]() est décroissante et converge aussi vers
est décroissante et converge aussi vers ![]() Pour tout
Pour tout ![]() :
:
(![]() )
) ![]()
![]()
![]()
Par ailleurs, en multipliant par ![]() l’inégalité de gauche dans
l’inégalité de gauche dans ![]() :
:
![]()
![]()
Ceci montre que la suite ![]() est croissante. La démarche est analogue pour la suite
est croissante. La démarche est analogue pour la suite ![]()

Supposons que ![]() n’admette aucun point fixe, c’est-à-dire que l’application
n’admette aucun point fixe, c’est-à-dire que l’application ![]() ne s’annule pas. Etant continue,
ne s’annule pas. Etant continue, ![]() doit être de signe constant, ce qui entraîne que
doit être de signe constant, ce qui entraîne que ![]() est de signe constant. Ainsi, la suite
est de signe constant. Ainsi, la suite ![]() est monotone. On a prouvé par contraposition que si cette suite n’est pas monotone, alors
est monotone. On a prouvé par contraposition que si cette suite n’est pas monotone, alors ![]() possède au moins un point fixe.
possède au moins un point fixe.
Par l’absurde. Supposons que la suite de terme général ![]() ne converge pas vers
ne converge pas vers ![]()
Il existe alors ![]() tel que :
tel que :
![]()
Le théorème de Bolzano-Weierstrass permet d’extraire de ![]() une sous-suite convergente
une sous-suite convergente ![]() de limite
de limite ![]() En passant à la limite dans l’inégalité
En passant à la limite dans l’inégalité
![]()
![]()

Dans ce qui suit, on notera ![]() la partie fractionnaire d’un réel
la partie fractionnaire d’un réel ![]()
La suite de terme général ![]() est à valeurs dans
est à valeurs dans ![]() donc l’ensemble
donc l’ensemble ![]() de ses valeurs d’adhérence est contenu dans
de ses valeurs d’adhérence est contenu dans ![]() Si l’on montre que
Si l’on montre que ![]() cela permettra de conclure que
cela permettra de conclure que ![]() Considérons donc
Considérons donc ![]()
L’idée de base est que si ![]() alors
alors ![]() mais il n’est pas question d’écrire
mais il n’est pas question d’écrire ![]() car l’application
car l’application ![]() n’est pas à valeurs entières ! Qu’à cela ne tienne …
n’est pas à valeurs entières ! Qu’à cela ne tienne …
Posons pour tout ![]() :
:
![]()
![]()
![]()
![]()
- est extraite de
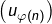 donc converge vers
donc converge vers 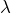
- est extraite de

ce qui prouve que ![]()

Soit ![]() une suite réelle quelconque. Considérons l’ensemble :
une suite réelle quelconque. Considérons l’ensemble :
![]()
![]()
On construit ainsi, par récurrence, une suite extraite ![]() strictement décroissante.
strictement décroissante.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
