Lettre D
DÉNOMBRABLE
Un ensemble ![]() est qualifié de dénombrable, par définition, lorsqu’il existe une bijection
est qualifié de dénombrable, par définition, lorsqu’il existe une bijection ![]() Bien entendu, dès qu’une telle bijection existe, on dispose de sa réciproque
Bien entendu, dès qu’une telle bijection existe, on dispose de sa réciproque ![]() On peut donc reformuler : est dit dénombrable tout ensemble « en bijection avec
On peut donc reformuler : est dit dénombrable tout ensemble « en bijection avec ![]() » .
» .
On peut montrer que chacun des ensembles suivants est dénombrable : ![]()
![]()
![]() et
et ![]()
Pour ![]() , c’est facile à justifier : l’application
, c’est facile à justifier : l’application ![]() est bijective.
est bijective.
Cet exemple se généralise : si ![]() est une partie finie de
est une partie finie de ![]() alors l’ensemble
alors l’ensemble ![]() (lire :
(lire : ![]() privé de
privé de ![]() qui est par définition constitué des entiers naturels qui n’appartiennent pas à
qui est par définition constitué des entiers naturels qui n’appartiennent pas à ![]() est dénombrable.
est dénombrable.
Pour ![]() c’est un peu moins évident : on s’en sort en énumérant les entiers relatifs « en zig-zag » . Autrement dit : 0, 1, -1, 2, -2, 3, -3, etc … Cette peut être formalisée en considérant l’application
c’est un peu moins évident : on s’en sort en énumérant les entiers relatifs « en zig-zag » . Autrement dit : 0, 1, -1, 2, -2, 3, -3, etc … Cette peut être formalisée en considérant l’application
![]()
En revanche ![]() n’est pas dénombrable. Une preuve de cette affirmation est donnée dans cet article de vulgarisation et vous pourrez suivre, dans la vidéo ci-dessous, pas moins de quatre preuve de ce résultat :
n’est pas dénombrable. Une preuve de cette affirmation est donnée dans cet article de vulgarisation et vous pourrez suivre, dans la vidéo ci-dessous, pas moins de quatre preuve de ce résultat :
Etant donné est un ensemble ![]() , il n’existe aucune surjection (et, en particulier, aucune bijection) de
, il n’existe aucune surjection (et, en particulier, aucune bijection) de ![]() vers
vers ![]() . On voit ainsi que
. On voit ainsi que ![]() est non dénombrable.
est non dénombrable.
La proposition suivante est fondamentale : si ![]() est une suite d’ensembles dénombrables, alors
est une suite d’ensembles dénombrables, alors ![]() est aussi dénombrable.
est aussi dénombrable.
Les challenges numéros 34, 49 et 73 entrent plus ou moins dans cette thématique. Vous êtes invité(e) à y réfléchir.
DENSE (partie)
Définition
Soient ![]() un espace vectoriel normé et soit
un espace vectoriel normé et soit ![]() On dit que
On dit que ![]() est dense dans
est dense dans ![]() lorsque tout vecteur de
lorsque tout vecteur de ![]() est la limite d’une suite convergente à termes dans
est la limite d’une suite convergente à termes dans ![]()
Remarque
Cette définition est présentée ainsi par souci de simplicité. Une version à la fois plus générale et plus officielle serait la suivante :
Soit ![]() un espace topologique et soit
un espace topologique et soit ![]() On dit que
On dit que ![]() est dense dans
est dense dans ![]() lorsque
lorsque ![]() (le symbole
(le symbole ![]() désigne l’adhérence de
désigne l’adhérence de ![]() dans
dans ![]()
Si la topologie de ![]() est métrisable (c’est-à-dire : s’il existe une distance
est métrisable (c’est-à-dire : s’il existe une distance ![]() sur
sur ![]() qui induit sa topologie), cette condition équivaut à l’existence, pour tout
qui induit sa topologie), cette condition équivaut à l’existence, pour tout ![]() d’une suite
d’une suite ![]() à termes dans
à termes dans ![]() qui converge vers
qui converge vers ![]() c’est-à-dire telle que :
c’est-à-dire telle que :
![]()
![]()
Exemple 1
Dans ![]() les parties suivantes sont denses :
les parties suivantes sont denses :
- l’ensemble
 des rationnels
des rationnels - l’ensemble
 des irrationnels
des irrationnels
Exemple 2
Dans ![]() les parties suivantes sont denses :
les parties suivantes sont denses :
- l’ensemble des matrice inversibles (qui est aussi un ouvert)
- l’ensemble des matrices diagonalisables

L’un des principaux intérêts de la notion de densité le suivant : pour démontrer une propriété donnée pour chaque élément d’un certain espace, il suffit parfois de l’établir pour les éléments d’une partie dense, puis de passer à la limite.
Voici quelques illustrations de cette idée :
- Si
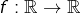 est continue et si
est continue et si 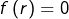 pour tout
pour tout 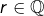 alors
alors 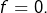
- Si
![Rendered by QuickLaTeX.com f\in\mathcal{C}\left(\left[0,1\right],\mathbb{R}\right)](https://math-os.com/wp-content/ql-cache/quicklatex.com-15f480ea4c0175622898313d0aa46f05_l3.png) vérifie
vérifie 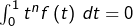 pour tout
pour tout 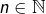 alors
alors 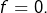 On peut voir (par linéarité) que
On peut voir (par linéarité) que 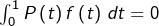 pour toute fonction polynomiale
pour toute fonction polynomiale 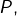 puis raisonner par densité grâce au théorème d’approximation uniforme de Weierstrass.
puis raisonner par densité grâce au théorème d’approximation uniforme de Weierstrass. - Si
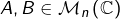 alors
alors 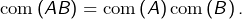 On peut d’abord le prouver pour les couples de matrices inversibles, puis utiliser la continuité de l’application
On peut d’abord le prouver pour les couples de matrices inversibles, puis utiliser la continuité de l’application 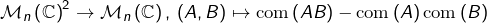 et le fait que
et le fait que 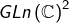 est une partie dense de
est une partie dense de 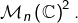
- Si
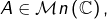 alors
alors 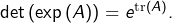 On peut prouver cela pour les matrices diagonalisables et utiliser ensuite la continuité du déterminant, de l’exponentielle (complexe et matricielle) et de la trace.
On peut prouver cela pour les matrices diagonalisables et utiliser ensuite la continuité du déterminant, de l’exponentielle (complexe et matricielle) et de la trace.
DIAGONALISABLE
Soit ![]() un
un ![]() espace vectoriel de dimension finie et soit
espace vectoriel de dimension finie et soit ![]()
Définition 1
![]() est dit diagonalisable lorsqu’il existe une base de
est dit diagonalisable lorsqu’il existe une base de ![]() formée de vecteurs propres pour
formée de vecteurs propres pour ![]() Dans une telle base,
Dans une telle base, ![]() est représenté par une matrice diagonale, d’où la terminologie.
est représenté par une matrice diagonale, d’où la terminologie.
Définition 2
Une matrice ![]() est dite diagonalisable dans
est dite diagonalisable dans ![]() (précision indispensable ! voir exemple ci-dessous) lorsque l’endomorphisme de
(précision indispensable ! voir exemple ci-dessous) lorsque l’endomorphisme de ![]() canoniquement associé à
canoniquement associé à ![]() est diagonalisable.
est diagonalisable.
Ceci revient à dire qu’il existe un couple ![]() tel que :
tel que :
![]()
Exemple
![]() est diagonalisable dans
est diagonalisable dans ![]() mais pas dans
mais pas dans ![]()
On note ![]() le spectre de
le spectre de ![]() et
et ![]() son polynôme caractéristique.
son polynôme caractéristique.
Pour chaque valeur propre ![]() on note :
on note :
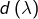 la dimension du sous-espace propre associé
la dimension du sous-espace propre associé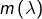 la multiplicité de
la multiplicité de 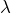 en tant que racine de
en tant que racine de 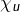
Théorème 1
![]() est diagonalisable si, et seulement si,
est diagonalisable si, et seulement si, ![]() est scindé dans
est scindé dans ![]() et de plus :
et de plus :
![]()
Corollaire
Si ![]() est scindé dans
est scindé dans ![]() et à racines simples, alors
et à racines simples, alors ![]() est diagonalisable.
est diagonalisable.
Par exemple, l’endomorphisme de ![]() canoniquement associé à la matrice triangulaire
canoniquement associé à la matrice triangulaire
![Rendered by QuickLaTeX.com \[A=\left[\begin{array}{cccc}0 & 1 & 1 & 1\\0 & 1 & 1 & 1\\0 & 0 & 2 & 1\\0 & 0 & 0 & 3\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5956ab1be6bb931beaf7b71d307b595f_l3.png)
Autre exemple, moins immédiat : toute matrice ![]() est la limite d’une suite de matrices diagonalisables dans
est la limite d’une suite de matrices diagonalisables dans ![]() . Autrement dit, l’ensemble des matrices diagonalisables dans
. Autrement dit, l’ensemble des matrices diagonalisables dans ![]() est une partie dense de
est une partie dense de ![]() .
.

Attention : Le corollaire ci-dessus ne donne qu’une condition suffisante (et pas du tout nécessaire) de diagonalisation. Par exemple, une homothétie est évidemment diagonalisable et possède pourtant une valeur propre multiple (en dimension ![]() ).
).
Théorème 2
![]() est diagonalisable si, et seulement s’il existe
est diagonalisable si, et seulement s’il existe ![]() scindé dans
scindé dans ![]() et à racines simples, tel que
et à racines simples, tel que ![]()
Par exemple : tout projecteur de ![]() est diagonalisable puisqu’annulé par
est diagonalisable puisqu’annulé par ![]() de même (en caractéristique différente de 2) toute symétrie de
de même (en caractéristique différente de 2) toute symétrie de ![]() est diagonalisable puisqu’annulée par
est diagonalisable puisqu’annulée par ![]()
DISTANCE (à une partie)
Définition
Soient un espace vectoriel normé ![]() et une partie non vide
et une partie non vide ![]() .
.
Pour tout ![]() , on note :
, on note :
![]()
Remarque
Cette définition s’étend naturellement aux espaces métriques, en remplaçant ![]() par la distance entre
par la distance entre ![]() et
et ![]()
Exemple 1
Dans ![]() si
si ![]() , alors pour tout
, alors pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[d\left(x,\left]a,b\right[\right)=\left\{ \begin{array}{cc}a-x & \text{si }x < a\\0 & \text{si }a\leqslant x \leqslant b\\x-b & \text{si }x > b\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4a0ca53b2dcaf4ffd4f4907c2b668ad5_l3.png)
Exemple 2
Dans ![]() muni de sa norme euclidienne, considérons
muni de sa norme euclidienne, considérons ![]() et
et ![]() et notons
et notons ![]() le disque fermé de centre
le disque fermé de centre ![]() et de rayon
et de rayon ![]() Alors, pour tout
Alors, pour tout ![]() , en notant :
, en notant :
![]()
![Rendered by QuickLaTeX.com \[d\left(\left(x,y\right),D\right)=\left\{ \begin{array}{cc}0 & \text{si }\rho\leqslant r\\\sqrt{\left(x-a\right)^{2}+\left(y-b\right)^{2}}-r & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c80742fa4cf55a2f79ed3004ac9eff68_l3.png)
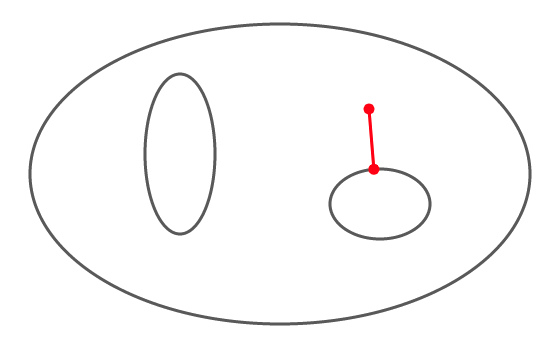
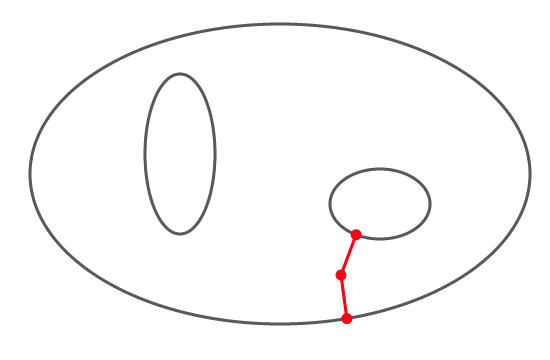
Dans l’illustration ci-dessous, ![]() est l’union de trois ellipses.
est l’union de trois ellipses.
Pour certains points, la distance à ![]() est atteinte une fois, pour d’autres deux fois. Il existe même deux points pour lesquelles elle est atteinte trois fois (on pourrait qualifier ces points de points triples) : l’un d’eux a été représenté; sauriez-vous localiser l’autre ?
est atteinte une fois, pour d’autres deux fois. Il existe même deux points pour lesquelles elle est atteinte trois fois (on pourrait qualifier ces points de points triples) : l’un d’eux a été représenté; sauriez-vous localiser l’autre ?
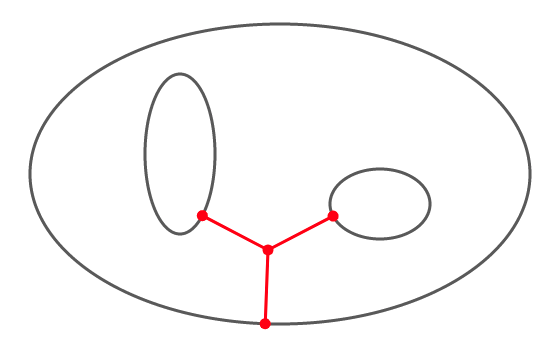
Voici quelques résultats de base, à connaître …
1 – Vecteurs à distance nulle. D’une manière générale :
![]()
En particulier, si ![]() est fermé alors les vecteurs qui sont à distance nulle de
est fermé alors les vecteurs qui sont à distance nulle de ![]() sont exactement les éléments de
sont exactement les éléments de ![]()
Sans cette hypothèse, il reste que ![]() mais l’implication réciproque est fausse. Par exemple, dans
mais l’implication réciproque est fausse. Par exemple, dans ![]() :
:
![]()
2 – Continuité. On peut montrer que l’application
![]()
![]()
On peut s’interroger sur la différentiabilité de ![]() , mais c’est une question plus délicate, qui fait intervenir les propriétés géométriques et topologiques de
, mais c’est une question plus délicate, qui fait intervenir les propriétés géométriques et topologiques de ![]()
3 – Distance atteinte. Si ![]() est un compact de
est un compact de ![]() alors (propriété générale d’une application continue sur un compact et à valeurs réelles), pour tout
alors (propriété générale d’une application continue sur un compact et à valeurs réelles), pour tout ![]() il existe
il existe ![]() tel que :
tel que :
![]()
Et sans hypothèse de compacité, l’existence d’un tel ![]() n’est pas assurée : considérer cette fois un disque ouvert
n’est pas assurée : considérer cette fois un disque ouvert ![]() de centre
de centre ![]() et de rayon
et de rayon ![]() ainsi qu’un point
ainsi qu’un point ![]() extérieur à
extérieur à ![]() Alors
Alors ![]() et cette distance n’est pas atteinte.
et cette distance n’est pas atteinte.
4 – Projection orthogonale. Dans le cadre des espaces préhilbertiens, le théorème de la projection orthogonale donne des informations sur la distance d’un vecteur à un sous-espace de dimension finie (ou, plus généralement, à une partie non vide, convexe et complète). Voir cet article.
DUPLICATION (trigonométrie)
En trigonométrie circulaire, les formules :
(1) ![]()
(2) ![]()
Grâce à la formule fondamentale ![]() la relation
la relation ![]() peut encore s’écrire :
peut encore s’écrire :
![]()
![]()
![]()
![]()
![]()
![]()
On a essentiellement la même chose en trigonométrie hyperbolique. En effet, pour tout ![]() :
:
(1′) ![]()
(2′) ![]()
![]()
![]()
![]()
![]()
![]()