Somme de cubes

Le bagage mathématique requis pour les trois premières sections de cet article est minimaliste : tout au plus, la connaissance de la formule donnant l’aire d’un rectangle (bon … disons que j’exagère, mais pas beaucoup).

De quoi s’agit-il ?

Vous allez observer une étonnante coïncidence : deux calculs, apparemment sans lien, qui donnent le même résultat. Il faudra alors s’interroger sur la raison de cette coïncidence et proposer une (ou plusieurs) explication(s).

  • Calcul n° 1 : le carré d’une somme du genre 1 + 2 + … + n, où n désigne un entier positif.
  • Calcul n° 2 : la somme des cubes de n premiers entiers.

A vos marques ! Prêt(e) ? C’est parti …

1 – Carré de la somme des premiers entiers

Commençons par évoquer un calcul qui vous est peut-être familier.

Si l’on ajoute les nombres entiers de 1 à 8, on trouve :

    \[1+2+3+4+5+6+7+8=36\]

Pour faire ce calcul, tel qu’il est écrit, il a fallu effectuer 7 additions.

Curieusement, on parvient au même résultat en effectuant, en tout et pour tout, 3 opérations :

    \[\frac{8\times\left(8+1\right)}{2}=36\]

Coïncidence, me direz-vous …

Pas du tout ! Vous pouvez refaire l’expérience avec une autre valeur que 8 et vous constaterez que ça marche encore. Sceptique ? Essayons avec 10 :

    \[1+2+3+4+5+6+7+8+9+10=55\]

et

    \[\frac{10\times\left(10+1\right)}{2}=55\]


Vous voyez ? ça a l’air de marcher … 🤗

Maintenant, il faut expliquer cela dans un cadre général (c’est-à-dire sans choisir une valeur particulière comme 8 ou 10). Nous allons utiliser une lettre, par exemple ‘n’, pour désigner un nombre entier quelconque, au moins égal à 1.

En ajoutant les entiers de 1 à n, on obtient un total : S=1+2+\cdots+\left(n-1\right)+n

idée-géniale

Astuce géniale, on va effectuer les additions en sens inverse, ce qui ne modifie évidemment pas le résultat :

    \[S=n+\left(n-1\right)+\cdots+2+1\]

On ajoute alors membre à membre les deux inégalités précédentes, pour obtenir :

    \[2S=\left[1+n\right]+\left[2+\left(n-1\right)\right]+\cdots+\left[\left(n-1\right)+2\right]+\left[n+1\right]\]

et vous constatez que les termes entre crochets sont tous égaux à n+1. Moralité :

    \[2S=n\left(n+1\right)\]

et donc :

    \[\fcolorbox{black}{myBlue}{$\displaystyle{S=\frac{n\left(n+1\right)}{2}}$}\]

Et voilà !

Un petit garçon, âgé de 7 ou 8 ans, aurait découvert cela tout seul, vers 1785. Il s’appelait Carl Friedrich Gauss. Pour en savoir plus à ce sujet, je vous invite à lire sur ma page LinkedIn un extrait du livre Les Arpenteurs du Monde, de Daniel Kehlmann (Ed. Babel).

2 – Somme des premiers cubes

A présent, essayons de calculer la somme :

    \[T=1^{3}+2^{3}+\cdots+n^{3}\]

Pour n=8, on trouve :

    \[1+8+27+64+125+216+343+512=1296\]

Curieusement, 1296=36^{2}, de sorte que :

    \[1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3=\left(1+2+3+4+5+6+7+8\right)^{2}\]

Un calcul similaire révèle que ça marche aussi avec n=10, puisque la somme des 10 premiers cubes vaut :

    \[1^{3}+2^{3}+\cdots+10^{3}=3025=55^{2}=\left(1+2+\cdots+10\right)^{2}\]

Ceci nous conduit naturellement à conjecturer (pour savoir ce qu’on appelle en maths une conjecture, voir cet article) que, pour tout entier n\geqslant1 :

    \[\boxed{1^{3}+2^{3}+\cdots+\left(n-1\right)^{3}+n^{3}=\left(1+2+\cdots+\left(n-1\right)+n\right)^{2}}\]

Si vous connaissez un peu l’usage de la notation \Sigma (et sinon, allez jeter un coup d’œil par ici), vous pourrez reformuler ce résultat de manière plus compacte :

(\star)   \[\fcolorbox{black}{myBlue}{$\displaystyle{\forall n\in\mathbb{N}^{\star},\quad\sum_{k=1}^{n}k^{3}=\left(\sum_{k=1}^{n}k\right)^{2}}$}\]

Nous allons apporter, dans les sections suivantes, trois preuves de cette affirmation.

3 – Preuve géométrique

Dans la figure ci-dessous, apparaît un grand carré dont le côté mesure 1+2+\cdots+n :

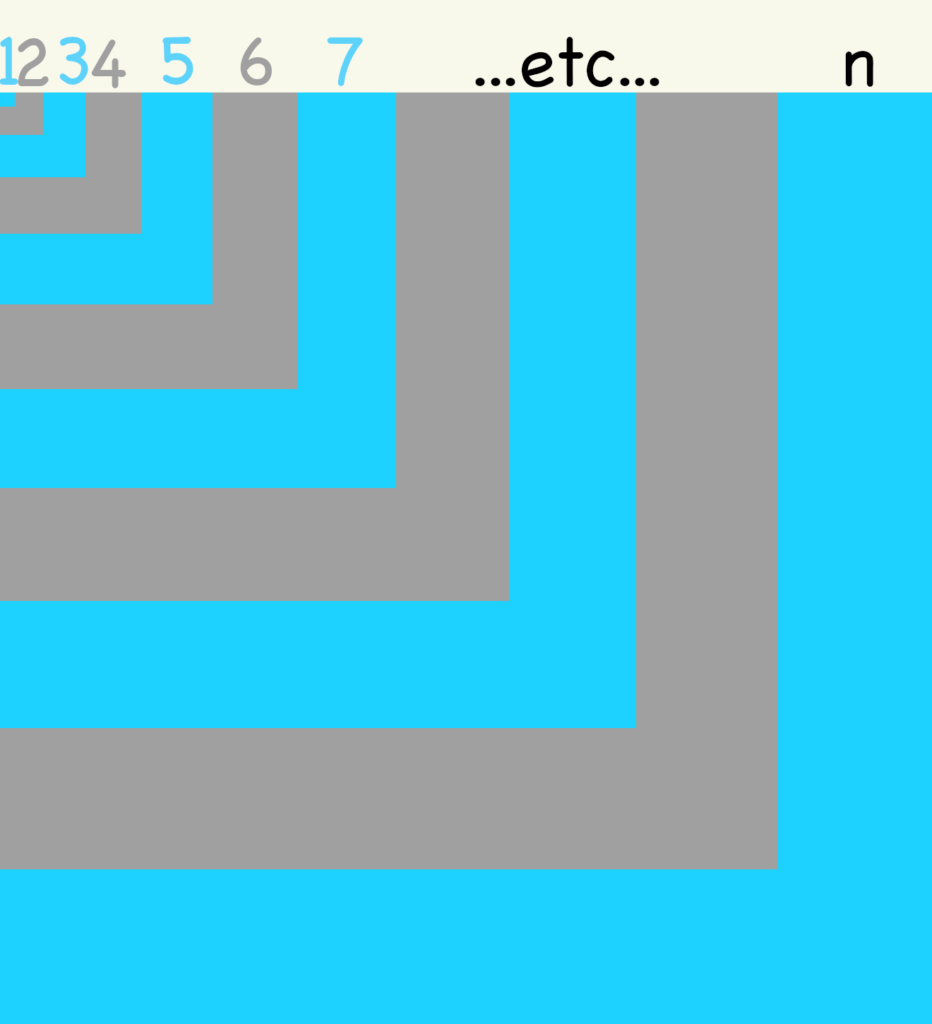
L’aire de ce carré est donc :

    \[\mathcal{A}=\left(1+2+\cdots+n\right)^{2}\]

Mais cette aire est aussi égale à la somme des aires des régions de couleurs (des ‘L’ inversés, alternativement bleus et gris).

Calculons l’aire de k-ème région. Dans le dessin qui suit, cette région a été décomposée en deux rectangles identiques (en noir) et un carré (en rouge) :

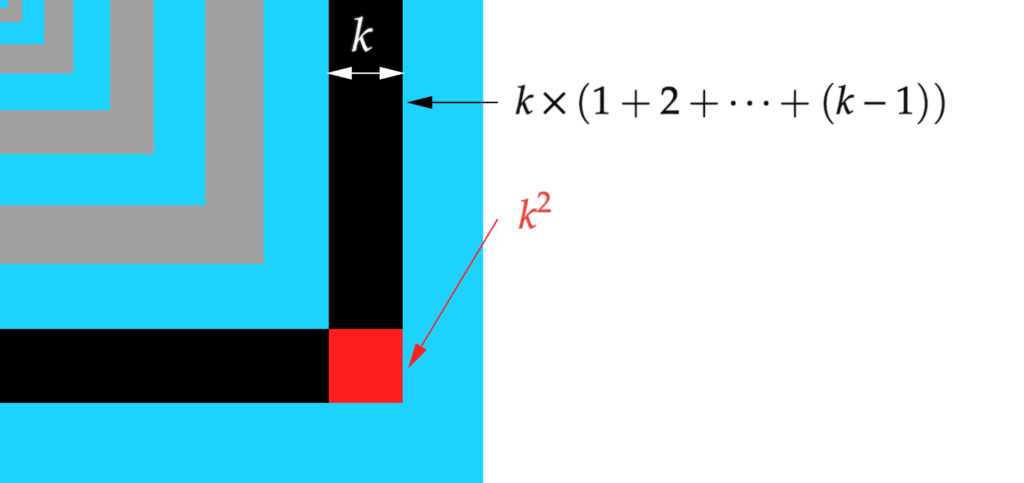
De toute évidence, l’aire du petit carré rouge est :

    \[\mathcal{A}_{carr\acute{e}}=k^{2}\]

Quant à l’aire d’un rectangle noir, elle est donnée par le produit des longueurs des côtés :

    \[\mathcal{A}_{rect}=k\left(1+2+\cdots\left(k-1\right)\right)\]

Or, nous savons calculer la sommes des k-1 premiers entiers (cf. section 1) et donc :

    \[\mathcal{A}_{rect}=k\;\frac{\left(k-1\right)k}{2}=\frac{k^{3}-k^{2}}{2}\]

Ainsi, l’aire de la k-ème région est donnée par :

    \[\mathcal{A}_{k}=2\:\mathcal{A}_{rect}+\mathcal{A}_{carr\acute{e}}=k^{3}\]

En définitive, vu que :

    \[\mathcal{A}=\mathcal{A}_{1}+\mathcal{A}_{2}+\cdots+\mathcal{A}_{n}\]

on conclut que :

    \[\left(1+2+\cdots+n\right)^{2}=1^{3}+2^{3}+\cdots+n^{3}\]

Nous avons prouvé notre conjecture 🤗🤗

4 – Preuve par récurrence

Si vous savez ce qu’est une démonstration par récurrence, il vous sera facile d’établir par ce procédé que :

(1)   \[\forall n\in\mathbb{N}^{\star},\quad1+2+\cdots+n=\frac{n\left(n+1\right)}{2}\]

et :

(2)   \[\forall n\in\mathbb{N}^{\star},\quad1^{3}+2^{3}+\cdots+n^{3}=\frac{n^{2}\left(n+1\right)^{2}}{4}\]

ce qui entraînera la formule \left(\star\right).

Détaillons la preuve de (2). On initialise facilement la récurrence :

    \[1^{3}=1=\frac{1^{2}\left(1+1\right)^{2}}{4}\]

Ensuite, en supposant vraie l’égalité pour un certain entier n\geqslant1, on voit que :

    \begin{eqnarray*}1^{3}+2^{3}+\cdots+n^{3}+\left(n+1\right)^{3} & = & \frac{n^{2}\left(n+1\right)^{2}}{4}+\left(n+1\right)^{3}\\& = & \left(n+1\right)^{2}\left(\frac{n^{2}}{4}+n+1\right)\\& = & \frac{1}{4}\left(n+1\right)^{2}\left(n^{2}+4n+4\right)\end{eqnarray*}

On reconnaît l’identité a^{2}+2ab+b^{2}=\left(a+b\right)^{2}, pour a=n et b=2 :

    \[n^{2}+4n+4=\left(n+2\right)^{2}\]

Ainsi :

    \[1^{3}+2^{3}+\cdots+n^{3}+\left(n+1\right)^{3}=\frac{\left(n+1\right)^{2}\left(n+2\right)^{2}}{4}\]

comme souhaité.

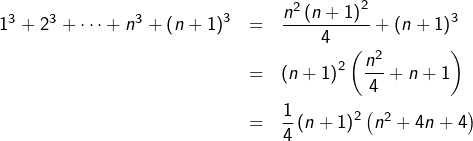
Et si vous ne savez pas bien comment faire une démonstration par récurrence, alors cet article-ci est fait pour vous !

5 – Une sommation télescopique

Le défaut de la démonstration par récurrence précédente est commun à toutes les démonstrations de cette nature : elles présupposent que l’on sache à l’avance ce qu’on veut prouver.

Voici un moyen de s’en sortir autrement, mais cela va nécessiter une petite astuce !

On va calculer de deux manières la somme :

    \[X_{n}=\sum_{k=1}^{n}\left[\left(k+1\right)^{4}-k^{4}\right]\]

D’une part, on observe que la sommation est télescopique, ce qui veut simplement dire que les termes se simplifient en cascade … Par exemple :

    \[X_{4}=\left[2^{4}-1^{4}\right]+\left[3^{4}-2^{4}\right]+\left[4^{4}-3^{4}\right]+\left[5^{4}-4^{4}\right]\]

et il ne reste, après simplification que : X_{4}=5^{4}-1. Plus généralement, on comprend ainsi que :

    \[\boxed{X_{n}=\left(n+1\right)^{4}-1}\]

D’autre part, on peut développer par la formule binôme :

    \[\left(k+1\right)^{4}=k^{4}+4k^{3}+6k^{2}+4k+1\]

et donc :

    \[\left(k+1\right)^{4}-k^{4}=4k^{3}+6k^{2}+4k+1\]

puis, après sommation pour k=1 à n :

    \[X_{n}=4\sum_{k=1}^{n}k^{3}+6\sum_{k=1}^{n}k^{2}+4\sum_{k=1}^{n}k+\sum_{k=1}^{n}1\]

Pour terminer, on a besoin de connaître la formule suivante :

    \[\sum_{k=1}^{n}k^{2}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\]

(dont la preuve peut être obtenue par récuurence ou, mieux, en suivant la même voie que pour la présente démonstration, c’est-à-dire en calculant de deux façons la somme {\displaystyle \sum_{k=1}^{n}\left[\left(k+1\right)^{3}-k^{3}\right]).}

Avec cela en poche, on obtient :

    \[\boxed{X_{n}=4\sum_{k=1}^{n}k^{3}+n\left(n+1\right)\left(2n+1\right)+2n\left(n+1\right)+n}\]

Après avoir confronté les deux expressions obtenues pour X_{n}, on conclut que :

    \[\sum_{k=1}^{n}k^{3}=\frac{1}{4}\left[\left(n+1\right)^{4}-1-n\left(n+1\right)\left(2n+1\right)-2n\left(n+1\right)-n\right]\]

Il reste un peu de calcul pour simplifier cette dernière expression (mais cela ne devrait soulever aucune difficulté). Je vous encourage à examiner cela en détail … et vous trouverez finalement (comme attendu) que :

    \[\sum_{k=1}^{n}k^{3}=\frac{n^{2}\left(n+1\right)^{2}}{4}=\left(\sum_{k=1}^nk\right)^2\]

Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article
    
Étiquettes : , , , , ,

La publication a un commentaire

  1. fabo34 1 Oct 2022 Répondre

    Bonjour,

    il y a également très simple en écrivant tout cube différence de 2 carrés, soit x³=(½x(x+1))²-(½x(x-1))²
    donc:
    n³=(½n(n+1))²-(½n(n-1))²
    (n-1)³=(½n(n-1))²-(½(n-1)(n-2))²
    (n-2)³=(½(n-1)(n-2))²-(½(n-2)(n-3))²
    …
    …
    2³= (½3*2))² -(½*2*1))²
    1³= (½*2*1))² – 0

    Somme telescopique, il ne reste que Sₙ=(½n(n+1))² !

    Bon ça ne fonctionne que pour les cubes, mais c’est quand même beau comme résultat!

Laisser un commentaire