
L’objet de cet article est d’établir la formule suivante :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{0}^{x}\dfrac{1-\cos\left(t\right)}{t}\thinspace dt=\ln\left(x\right)+\gamma+\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be222a55f067f90a6ae71d707797f35c_l3.png)
Un certain nombre de détails techniques devront être examinés avant de pouvoir établir ce résultat, ce qui sera fait à la section 4.
1 – Existence des deux intégrales
Etant donné ![]() l’application
l’application ![]() est continue et possède en
est continue et possède en ![]() une limite finie, qui est nulle. On peut justifier cela en observant que cette fraction est égale, au signe près, au taux d’accroissement du cosinus en
une limite finie, qui est nulle. On peut justifier cela en observant que cette fraction est égale, au signe près, au taux d’accroissement du cosinus en ![]() or :
or :
![]()
Quant à l’intégrale ![]() elle converge (quoique non absolument), ce qu’on peut voir au moyen d’une intégration par parties. En effet, pour tout
elle converge (quoique non absolument), ce qu’on peut voir au moyen d’une intégration par parties. En effet, pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
Si la notion d’intégrale impropre n’est pas claire, on pourra se reporter à cet article.
2 – Une somme trigonométrique
On aura besoin du petit résultat suivant :
Proposition
Pour tout entier ![]() et pour tout réel
et pour tout réel ![]() non multiple de
non multiple de ![]() :
:
(![]() )
) ![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}\sin\left(\left(2k+1\right)\theta\right)=\dfrac{1-\cos\left(2n\theta\right)}{2\sin\left(\theta\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cfe5afef3f9399c70674665658c669ab_l3.png)
Pour le démontrer, le plus simple consiste à multiplier le membre de gauche par ![]() et utiliser une formule de trigonométrie. On sait que, pour tout couple
et utiliser une formule de trigonométrie. On sait que, pour tout couple ![]() de nombres réels :
de nombres réels :
![]()
![Rendered by QuickLaTeX.com \[2\sin\left(\theta\right)\sum_{k=0}^{n-1}\sin\left(\left(2k+1\right)\theta\right)=\sum_{k=0}^{n-1}\left[\cos\left(2k\theta\right)-\cos\left(2\left(k+1\right)\theta\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-46b8bc68734f75495b1e3c7b2d3f35ed_l3.png)
![Rendered by QuickLaTeX.com \[2\sin\left(\theta\right)\sum_{k=0}^{n-1}\sin\left(\left(2k+1\right)\theta\right)=1-\cos\left(2n\theta\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c29639c993c0780b9fe46a29616e8d82_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}e^{i\left(2k+1\right)\theta}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-019d1bdb7f92746e9551e457bb05fbf0_l3.png)
Les calculs correspondants sont laissés au lecteur motivé 🙂
3 – Egalité à une constante près
Posons, pour tout ![]() :
:
![]()
![]()
![]()
4 – Un découpage astucieux
Afin de déterminer la constante ![]() on va calculer
on va calculer ![]()
En posant la changement de variable ![]() on voit que pour tout
on voit que pour tout ![]() :
:
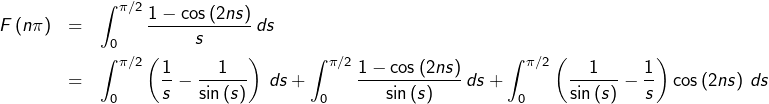
![]()
![]()
![Rendered by QuickLaTeX.com \[ B_{n}=2\sum_{k=0}^{n-1}\int_{0}^{\pi/2}\sin\left(\left(2k+1\right)s\right)\thinspace ds=2\sum_{k=0}^{n-1}\dfrac{1}{2k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b508ab7713c082189109885d245aac29_l3.png)
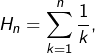 et vu que :
et vu que : ![]()
![]()
![]()
Tout ceci conduit au développement asymptotique :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall x>0,\thinspace\int_{0}^{x}\dfrac{1-\cos\left(t\right)}{t}\thinspace dt=\ln\left(x\right)+\gamma+\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c7bca8c3b04b759bbb35ff38875d938b_l3.png)
J’espère que cet article vous a plu. Si vous connaissez un nom officiel pour pour cette formule remarquable ou bien des applications significatives, merci de laisser un commentaire ci-dessous ou bien de me joindre en utilisant le formulaire de contact.

Bonjour Fabrice, merci pour la référence. J’avais déjà repéré l’article de Gourdon et Sebbah duquel ces formules sont extraites. J’en fais mention vers la fin de cette vidéo : https://youtu.be/bN_0VXEC8vo
Bonjour Monsieur,
Merci pour cet article !
Sur ce forum :
https://les-mathematiques.net/vanilla/index.php?p=discussion/comment/583251#Comment_583251
on trouve un pdf listant des formules, et l’une d’elle est celle de votre article en remplaçant cos(t) par exp(-t), il est ensuite précisé que cette autre formule est utile pour obtenir des décimales de la constante d’Euler. Je ne réponds pas précisément à votre demande d’application puisqu’il s’agit d’une « formule sœur » qui a une application, mais je n’ai trouvé que cela !
Bien à vous,
Oncle_Junior