
1 – Les quantificateurs (en 2 minutes …)
La plupart des énoncés mathématiques que nous manipulons comportent des quantificateurs.
Oui, vous savez bien … ces petits symboles ésotériques qui ressemblent soit à un ‘A’ renversé, soit à un ‘E’ vu dans un miroir.
Rappelons brièvement de quoi il s’agit, en donnant deux exemples très simples.
Exemple 1
Pour exprimer, avec des symboles, la phrase « le carré de tout nombre réel est positif ou nul », on écrit :
![]()
Exemple 2
Quant à la phrase « il existe un nombre réel positif dont le carré est égal à 2 », voici sa version formalisée :
![]()
Dans chacun des deux cas, le symbole (![]() ou
ou ![]() ) peut être choisi librement … tant qu’il ne s’agit pas d’un symbole déjà utilisé dans le contexte !
) peut être choisi librement … tant qu’il ne s’agit pas d’un symbole déjà utilisé dans le contexte !
Terminologie
Le symbole ![]() se lit « quel que soit » ou « pour tout » : c’est le quantificateur universel.
se lit « quel que soit » ou « pour tout » : c’est le quantificateur universel.
Le symbole ![]() se lit « il existe » : c’est le quantificateur existentiel. Il signifie, plus précisément : « il existe au moins »
se lit « il existe » : c’est le quantificateur existentiel. Il signifie, plus précisément : « il existe au moins »
Dans certaines circonstances, deux quantificateurs se suivent … et se ressemblent !
Par exemple, la phrase « pour tout entier naturel ![]() et pour tout réel positif
et pour tout réel positif ![]() la puissance
la puissance ![]() ème de
ème de ![]() est minorée (au sens large) par
est minorée (au sens large) par ![]() » devient, en symboles :
» devient, en symboles :
![]()
![]()
Pour le quantificateur existentiel, c’est le même topo.
Bref, on peut librement échanger deux quantificateurs qui se suivent lorsque ceux-ci sont de même nature (deux fois ![]() ou bien deux fois
ou bien deux fois ![]() ).
).

Mais si nos deux quantificateurs se suivent … et ne se ressemblent pas, alors les choses se compliquent …
2 – Quel que soit, il existe … ou le contraire ?
Considérons l’exemple suivant :
![]()
C’est évidemment vrai : il suffit de choisir ![]() (par exemple) et le tour est joué.
(par exemple) et le tour est joué.
Maintenant, intervertissons les quantificateurs …
L’énoncé précédent fait place à celui-ci :
![]()
Cet exemple montre bien que l’interversion de deux quantificateurs distincts (un ![]() et un
et un ![]() ) n’est pas neutre. Elle peut transformer un énoncé vrai en un énoncé faux et vice versa.
) n’est pas neutre. Elle peut transformer un énoncé vrai en un énoncé faux et vice versa.
Formulons à présent une remarque assez générale.
Remarque
Considérons deux ensembles ![]() et une propriété
et une propriété ![]() portant sur les couples
portant sur les couples ![]() d’éléments du produit cartésien
d’éléments du produit cartésien ![]()
Lorsqu’on écrit ![]() cela signifie que le couple
cela signifie que le couple ![]() appartient à
appartient à ![]() et qu’il vérifie la propriété en question.
et qu’il vérifie la propriété en question.
Intéressons-nous aux énoncés :
![]()
![]()
Si l’énoncé ![]() est vrai, alors l’énoncé
est vrai, alors l’énoncé ![]() l’est certainement aussi !
l’est certainement aussi !
Pour le dire en des termes simples : s’il existe dans ![]() un
un ![]() « universel », c’est-à-dire un
« universel », c’est-à-dire un ![]() qui convient à tous les
qui convient à tous les ![]() alors évidemment, pour chaque
alors évidemment, pour chaque ![]() particulier dans
particulier dans ![]() on peut trouver un
on peut trouver un ![]() dans
dans ![]() qui fera l’affaire (il suffit de prendre pour
qui fera l’affaire (il suffit de prendre pour ![]() ce fameux
ce fameux ![]()
En revanche, l’implication réciproque peut être en défaut. En effet, ce n’est pas parce qu’on peut toujours trouver un ![]() « local » (c’est-à-dire trouver, pour chaque
« local » (c’est-à-dire trouver, pour chaque ![]() de
de ![]() un
un ![]() qui convient … et qui dépendra a priori de ce
qui convient … et qui dépendra a priori de ce ![]() que l’on peut pour autant affirmer l’existence d’un
que l’on peut pour autant affirmer l’existence d’un ![]() « universel » au sens précédent.
« universel » au sens précédent.
Pourtant, l’interversion de quantificateurs est parfois valide … et peut révéler quelque chose de profond. C’est ce que nous allons maintenant détailler dans quatre contextes assez différents.
3 – Permutations d’ordre fini
Peut-être avez-vous jeté un coup d’œil au dernier exercice de cette fiche ?
Nous allons utiliser les mêmes notations…
On considère donc un ensemble ![]() ainsi qu’une application
ainsi qu’une application ![]()
Pour tout ![]() on note
on note ![]() la
la ![]() ème itérée de
ème itérée de ![]()
Par sécurité, rappelons que (par définition) :
![]()
c’est-à-dire, pour formuler les choses simplement :
![]()
![]()
![]()
Sont-ils équivalents ? Conformément à ce qui a été dit dans la remarque qui termine la section 2, il est clair que
Autant le dire tout de suite, l’implication ![]() n’est pas vraie en toute généralité.
n’est pas vraie en toute généralité.
Et pour s’en convaincre, rien de tel qu’un contre-exemple :
Prenons ![]() et l’application :
et l’application :
![]()
Dans le cadre de l’étude des groupes symétriques
Ici, ![]() désigne la permutation de
désigne la permutation de ![]() qui :
qui :
- laisse 1 fixe,
- envoie 2 sur 3 et 3 sur 2
- envoie 4 sur 5, 5 sur 6 et 6 sur 4
- envoie 7 sur 8, 8 sur 9, 9 sur 10 et 10 sur 7
- et ainsi de suite …
Il est facile de comprendre que ![]() vérifie
vérifie ![]()
Vite fait : chaque entier ![]() appartient au support de l’un des cycles, disons le cycle
appartient au support de l’un des cycles, disons le cycle ![]() où
où ![]() désigne le
désigne le ![]() ème nombre triangulaire :
ème nombre triangulaire :
![]()
Mais ![]() ne vérifie pas
ne vérifie pas ![]() car peu importe l’entier
car peu importe l’entier ![]() considéré, si l’entier
considéré, si l’entier ![]() est assez grand, il appartiendra au support d’un cycle de longueur
est assez grand, il appartiendra au support d’un cycle de longueur ![]() et fatalement, on aura
et fatalement, on aura ![]()
Cependant :
Proposition
Si E est supposé fini, alors les énoncés ![]() et
et ![]() sont équivalents !
sont équivalents !
Preuve (cliquer pour déplier / replier)
Observons déjà que si, pour un certain couple ![]() on a
on a ![]() alors
alors ![]() pour tout
pour tout ![]() (en d’autres termes, si l’exposant
(en d’autres termes, si l’exposant ![]() convient pour
convient pour ![]() alors tout exposant multiple de
alors tout exposant multiple de ![]() convient aussi).
convient aussi).
Maintenant, posons ![]() et, pour chaque
et, pour chaque ![]() notons :
notons :
![]()
Alors, en posant
![]()
Et si vous êtes gêné(e) par cette histoire de ppcm, il vous suffit de poser plutôt
4 – Caractérisation des homothéties
Cette section et la suivante supposent que vous connaissiez un peu d’algèbre linéaire : notions d’espace vectoriel, de famille libre ou liée et d’endomorphisme …
On considère :
- un
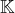 -espace vectoriel
-espace vectoriel  (dont le vecteur nul est noté
(dont le vecteur nul est noté 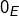 ),
), - un endomorphisme
 de
de 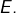
Rappel : les homothéties de ![]() sont les endomorphismes de la forme
sont les endomorphismes de la forme ![]() (pour
(pour ![]() arbitraire).
arbitraire).
Cela dit, considérons les deux énoncés suivants, qui concernent notre endomomorphisme ![]() :
:
![]()
![]()
L’implication
Nous allons prouver que l’implication ![]() est aussi vraie, ce qui nous donnera un nouvel exemple d’interversion de quantificateurs. Mais pour cela, il va falloir bosser un peu…
est aussi vraie, ce qui nous donnera un nouvel exemple d’interversion de quantificateurs. Mais pour cela, il va falloir bosser un peu…
Pour commencer, observons que sous l’hypothèse ![]() si
si ![]() alors il existe un unique
alors il existe un unique ![]() tel que
tel que ![]() Par conséquent, on dispose de l’application qui à tout vecteur non nul
Par conséquent, on dispose de l’application qui à tout vecteur non nul ![]() associe cet unique scalaire. Ce dernier peut être noté
associe cet unique scalaire. Ce dernier peut être noté ![]()
Pour conclure que ![]() est vraie, il suffit de prouver que l’application
est vraie, il suffit de prouver que l’application ![]() est constante. Pour cela, considérons un couple
est constante. Pour cela, considérons un couple ![]() de vecteurs non nuls et montrons que
de vecteurs non nuls et montrons que ![]() en distinguant deux cas :
en distinguant deux cas :
Premier cas : la famille 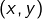 est libre
est libre
Nécessairement ![]() On peut donc écrire :
On peut donc écrire :
![]()
![]()
Il s’ensuit que :
![]()
![]()
En particulier : ![]()
Deuxième cas : la famille  est liée
est liée
Il existe alors ![]() tel que
tel que ![]() On a d’une part :
On a d’une part :
![]()
![]()
Par conséquent :
![]()
L’équivalence des énoncés ![]() et
et ![]() est établie.
est établie.
5 – Endomorphismes nilpotents
A nouveau, on considère un endomorphisme ![]() d’un
d’un ![]() espace vectoriel
espace vectoriel ![]()
Cette fois, les deux énoncés qui nous occupent sont :
![]()
![]()
L’énoncé
De nouveau, et toujours avec la remarque qui termine la section 2, on voit que : ![]()
Montrons que l’implication réciproque est vraie, sous l’hypothèse que ![]() est de dimension finie. Fixons pour cela une base
est de dimension finie. Fixons pour cela une base ![]() de
de ![]() et appliquons l’hypothèse
et appliquons l’hypothèse ![]() :
:
Pour chaque ![]() il existe un entier naturel non nul
il existe un entier naturel non nul ![]() tel que
tel que ![]() Notons
Notons ![]() le plus petit tel entier et posons :
le plus petit tel entier et posons :
![]()
Pour tout ![]() puisque
puisque ![]() et vu que
et vu que ![]() on voit que
on voit que ![]()
Soit maintenant ![]() un vecteur quelconque de
un vecteur quelconque de ![]() En décomposant
En décomposant ![]() dans la base
dans la base ![]() sous la forme
sous la forme 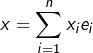 , on constate que :
, on constate que :
![Rendered by QuickLaTeX.com \[u^{Q}\left(x\right)=\sum_{i=1}^{n}x_{i}\thinspace u^{Q}\left(e_{i}\right)=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-27ab5054ec9c140a740c0348e5b33ca7_l3.png)
Ajoutons que, lorsque ![]() est de dimension infinie, l’implication
est de dimension infinie, l’implication ![]() devient fausse !
devient fausse !
Contre-exemple en dimension infinie
Prenons pour ![]() l’espace
l’espace ![]() des polynômes à une indéterminée et à coefficients dans
des polynômes à une indéterminée et à coefficients dans ![]() et pour
et pour ![]() l’endomorphisme de dérivation.
l’endomorphisme de dérivation.
La dérivation d’un polynôme (non constant) faisant chuter son degré d’un unité, la condition ![]() est remplie : en dérivant un quelconque polynôme un nombre suffisant de fois, on finit par tomber sur le polynôme nul.
est remplie : en dérivant un quelconque polynôme un nombre suffisant de fois, on finit par tomber sur le polynôme nul.
Pour autant, l’endomorphisme de dérivation n’est pas nilpotent puisqu’il existe de polynômes de degré arbitrairement grand.
6 – Continuité vs. continuité uniforme
Cette dernière section suppose connue la définition de la continuité d’une fonction numérique. Une certaine familiarité avec la notion de continuité uniforme vous facilitera les choses, mais elle ne s’impose pas puisque tout est défini ci-dessous.
Soit ![]() un intervalle non trivial de
un intervalle non trivial de ![]() (« non trivial », c’est-à-dire ni vide, ni réduit à un singleton) et soit
(« non trivial », c’est-à-dire ni vide, ni réduit à un singleton) et soit ![]() une application.
une application.
Voici deux énoncés qui concernent ![]() :
:
![]()
et
![]()
L’énoncé
L’énoncé ![]() dit que f est uniformément continue (toujours par définition).
dit que f est uniformément continue (toujours par définition).
Ces deux énoncés ne sont pas équivalents en général (c’est-à-dire sans hypothèse particulière sur ![]() ). On peut le voir en considérant l’application
). On peut le voir en considérant l’application
![]()
![]()
![]()
![]()
Cependant, si ![]() est un segment (intervalle fermé et borné), alors l’implication
est un segment (intervalle fermé et borné), alors l’implication ![]() est vraie : c’est le théorème de Heine.
est vraie : c’est le théorème de Heine.
Pour en savoir plus à ce sujet, voir cet article, consacré à la notion de convergence uniforme.
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
