Parties d’un ensemble fini

Avertissement – Dans ce texte, quelques unes des propriétés des coefficients binomiaux sont utilisées, notamment la formule du binôme de Newton ou encore celle qui exprime la symétrie de ces coefficients.

Il pourra donc être utile, au préalable, d’aller jeter un coup d’œil à cet article.

On examine ici quelques questions de combinatoire, qui gravitent autour du dénombrement des parties d’un ensemble fini.

Pour commencer, on fixe un cadre et quelques notations.

E désignera un ensemble fini. On notera n son cardinal (c’est-à-dire le nombre d’éléments de E). Les sous-ensembles de E, qu’on appelle aussi les parties de E, forment un ensemble noté \mathcal{P}\left(E\right).

Si k est un entier compris entre 0 et n, alors les parties de E ayant pour cardinal k forment un sous-ensemble de \mathcal{P}\left(E\right), noté \mathcal{P}_{k}\left(E\right). Par définition (cf. l’article signalé plus haut) :

    \[\fcolorbox{black}{myBlue}{$\text{card}\left(\mathcal{P}_{k}(E)\right)=\binom{n}{k}$}\]

1 – Combien de parties ?

Pour dénombrer les parties de E, c’est-à-dire calculer le cardinal de \mathcal{P}\left(E\right), on envisagera les trois points de vue suivants :

➡ Premier point de vue [ en bref ]

En examinant de petites valeurs de n, on peut aisément conjecturer la formule correcte, puis l’établir rigoureusement par récurrence.

➡ Second point de vue [ en bref ]

On peut s’appuyer sur le fait que \mathcal{P}\left(E\right) est l’union disjointe des \mathcal{P}_{k}\left(E\right) pour 0\leqslant k\leqslant n, passer aux cardinaux puis utiliser la formule du binôme.

➡ Troisième point de vue [ en bref ]

On peut mettre \mathcal{P}\left(E\right) en bijection avec un ensemble, dont le cardinal est déjà connu.

Le premier et le troisième point de vue sont exposés dans cette vidéo. Tous trois sont détaillés dans la suite de cet article.

Premier point de vue

➡ Si \text{card}(E)=0, autrement dit si E=\emptyset, alors E possède une seule partie, à savoir \emptyset.

➡ Si \text{card}(E)=1 (E est un singleton), alors E possède deux parties, à savoir \emptyset et E.

➡ Si \text{card}(E)=2 (E est une paire), alors on voit, en notant E=\left\{ a,b\right\} , que E possède quatre parties :

    \[\emptyset,\quad\left\{ a\right\} ,\quad\left\{ b\right\} ,\quad\left\{ a,b\right\}\]


Effectuons un pas de plus …

➡ Si \text{card}(E)=3, alors en notant E=\left\{ a,b,c\right\} , il apparaît que E possède huit parties, à savoir :

    \[\emptyset,\quad\left\{ a\right\} ,\quad\left\{ b\right\} ,\quad\left\{ c\right\} ,\quad\left\{ a,b\right\} ,\quad\left\{ a,c\right\} ,\quad\left\{ b,c\right\} ,\quad\left\{ a,b,c\right\}\]

Or il se trouve que :

    \[1=2^{0},\quad2=2^{1},\quad4=2^{2}\quad\text{et}\quad8=2^{3}\]

il est donc tentant de formuler une …

Conjecture

Si E est un ensemble de cardinal n, alors :

    \[\fcolorbox{black}{myBlue}{$\text{Card}\left(\mathcal{P}\left(E\right)\right)=2^{n}$}\]

Une conjecture qui va rapidement se métamorphoser en théorème !

Prouver cela, rien de tel qu’une bonne vieille récurrence.

Concernant la notion de preuve par récurrence, je vous invite (si besoin) à consulter cet article et / ou cet article plus avancé.

Notons \mathcal{H}_{n} l’assertion selon laquelle tout ensemble de cardinal n possède 2^{n} parties.

Nous avons vu plus haut que l’assertion \mathcal{H}_{0} est vraie en constatant que l’ensemble vide possède une seule partie ! Ceci initialise la récurrence et l’on peut passer à la preuve de l’hérédité.

Supposons \mathcal{H}_{n} vraie pour un certain n\in\mathbb{N}, et soit E un ensemble de cardinal n+1.

Notons a un élément de E et distinguons, parmi les parties de E :

➣ celles qui contiennent a,
➣  celles qui ne contiennent pas a.

Plus précisément, notons P_{a} l’ensemble des parties de E qui contiennent a.

Alors, l’application

    \[\varphi\thinspace:\thinspace P_{a}\rightarrow\mathcal{P}\left(E-\left\{ a\right\} \right),\:X\mapsto X-\left\{ a\right\}\]

est une bijection. En effet, en considérant \psi\thinspace:\thinspace\mathcal{P}\left(E-\left\{ a\right\} \right)\rightarrow P_{a},\thinspace Y\mapsto Y\cup\left\{ a\right\} , on constate que :

    \[\psi\circ\varphi=id_{P_{a}}\qquad\text{et}\qquad\varphi\circ\psi=id_{\mathcal{P}\left(E-\left\{ a\right\} \right)}\]

ce qui prouve que \varphi et \psi sont bijectives (et réciproques l’une de l’autre).

Par conséquent :

    \[\text{card}\left(P_{a}\right)=\text{card}\left(\mathcal{P}\left(E-\left\{ a\right\} \right)\right)\]

Quant à l’ensemble des parties de E qui ne contiennent pas  a, il s’agit de \mathcal{P}\left(E-\left\{ a\right\} \right) et l’hypothèse de récurrence permet d’affirmer que \text{card}\left(\mathcal{P}\left(E-\left\{ a\right\} \right)\right)=2^{n}.

Pour finir, comme le cardinal de l’union de deux ensembles finis et disjoints est égal à la somme de leurs cardinaux :

    \[\text{card}\left(\mathcal{P}\left(E\right)\right)=\text{card}\left(P_{a}\right)+\text{card}\left(\mathcal{P}\left(E-\left\{ a\right\} \right)\right)=2^{n}+2^{n}\]

c’est-à-dire \text{card}\left(\mathcal{P}\left(E\right)\right)=2^{n+1}, comme souhaité.

Second point de vue

Pour tout k\in\llbracket0,n\rrbracket, le nombre de parties de E qui sont de cardinal k est donné par :

    \[\text{card}\left(\mathcal{P}_{k}\left(E\right)\right)=\binom{n}{k}\]

Or, il est clair que :

    \[ \mathcal{P}\left(E\right)=\bigsqcup_{k=0}^{n}\mathcal{P}_{k}\left(E\right)\]

où \sqcup est le symbole pour l’union disjointe. Par conséquent :

    \[ \text{card}\left(\mathcal{P}\left(E\right)\right)=\sum_{k=0}^{n}\text{card}\left(\mathcal{P}_{k}\left(E\right)\right)=\sum_{k=0}^{n}\binom{n}{k}\]

On invoque à présent la formule du binôme, pour conclure que :

    \[\text{card}\left(\mathcal{P}\left(E\right)\right)=\sum_{k=0}^{n}\binom{n}{k}1^{k}1^{n-k}=\left(1+1\right)^{n}=2^{n}\]

Troisième point de vue

On peut montrer que si X et Y sont deux ensembles finis, alors il existe exactement \text{card }\left(Y\right)^{\text{card }\left(X\right)} applications de X vers Y. C’est d’ailleurs de là que provient la notation Y^{X} pour désigner l’ensemble de ces applications (même lorsque l’un au moins des ensembles X ou Y est infini).

Pour toute partie A de E, on définit sa fonction indicatrice, à savoir l’application \mathds{1}_A:E\mapsto\left\{0,1\right\} qui, à tout e\in E associe 1 si e\in A et 0 dans le cas contraire.

En associant sa fonction indicatrice à chaque partie A de E, on définit l’application :

    \[\Phi:\mathcal{P}\left(E\right)\rightarrow\left\{0,1\right\} ^{E},\thinspace A\mapsto\mathds{1}_{A}\]

Si l’on prouve que \Phi est bijective, il en résultera que :

    \[\text{card}\left(\mathcal{P}\left(E\right)\right)=\text{card}\left(\left\{ 0,1\right\} ^{E}\right)=2^{n}\]

Pour cela, on peut considérer l’application :

    \[\Psi:\left\{ 0,1\right\} ^{E}\rightarrow\mathcal{P}\left(E\right),\thinspace f\mapsto f^{-1}\left\langle \left\{ 1\right\} \right\rangle\]

où f^{-1}\left\langle \left\{ 1\right\} \right\rangle désigne l’image réciproque du singleton \left\{ 1\right\} par f, c’est-à-dire l’ensemble des éléments de E dont l’image par f est 1.

Si vous n’êtes pas à l’aise avec la notion d’image directe ou réciproque d’une partie par une application, je vous invite à lire (ou au moins à parcourir) cet article.

Il est alors facile de se convaincre que :

    \[\Psi\circ\Phi=id_{\mathcal{P}\left(E\right)}\qquad\text{et}\qquad\Phi\circ\Psi=id_{\left\{ 0,1\right\} ^{E}}\]

et ceci entraîne que \Phi et \Psi sont des bijections (chacune étant la réciproque de l’autre : cet argument a déjà été utilisé, dans un autre contexte, pour le premier point de vue).

La démonstration est terminée, mais il se peut que vous la trouviez un peu trop abstraite… Si tel est le cas, pas de panique ! Je vais essayer de rendre les choses plus « visuelles ».

Envisageons le cas particulier où E est de cardinal 3 et posons : E=\left\{ a,b,c\right\} . L’ensemble \mathcal{P}\left(E\right) est donc de cardinal 8 (cf. début de cette section). Cet ensemble est représenté ci-dessous dans le cadre de gauche.

Quant à l’ensemble \left\{ 0,1\right\} ^{E}, il comporte aussi 8 éléments : ce sont les applications de \left\{ a,b,c\right\} vers \left\{ 0,1\right\} , représentées chacune par un petit diagramme à l’intérieur du cadre de droite.

A chacune des huit parties de E, représentées en bleu dans les cases du cadre de gauche, l’application \Phi associe sa fonction indicatrice, qui est une application de E vers \left\{ 0,1\right\} , représentée (également en bleu) dans la case homologue (même ligne et même colonne) du cadre de droite.

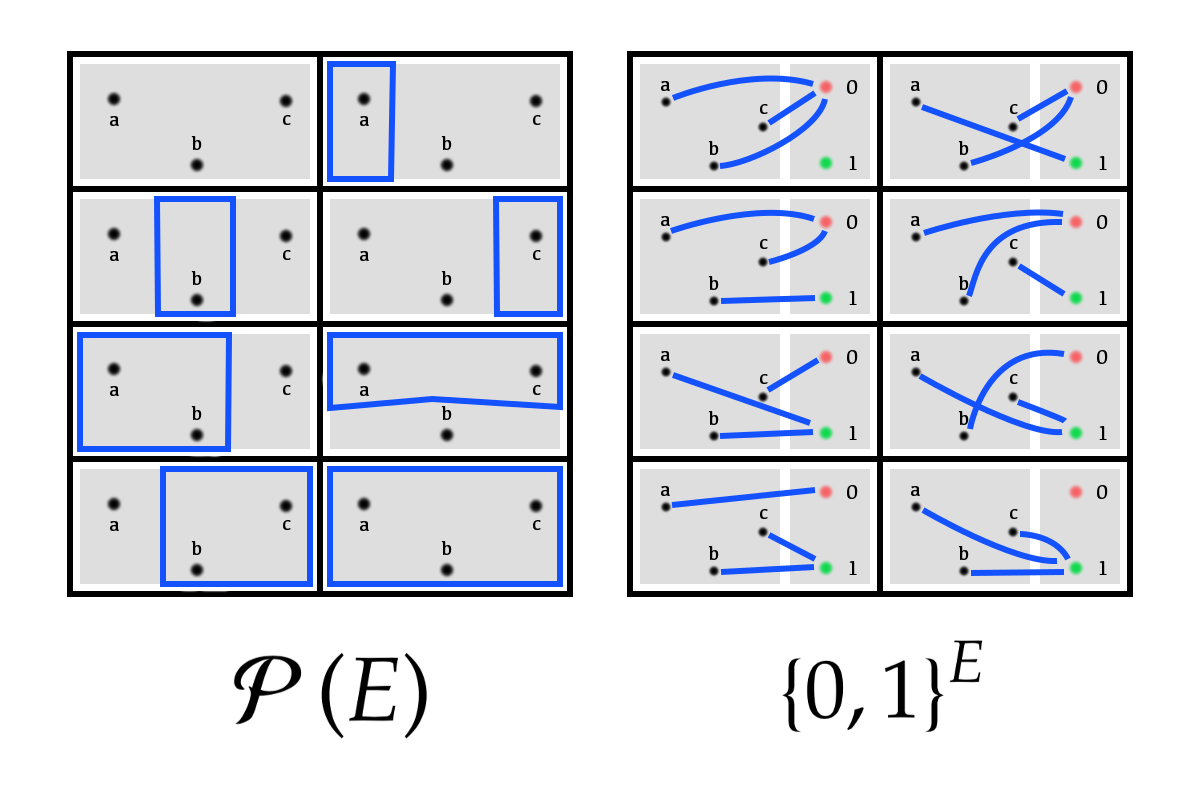
Par exemple, la partie \left\{a,b\right\} apparaît à la ligne 3 / colonne 1 du cadre de gauche et sa fonction indicatrice apparaît au même emplacement de celui de droite.

2 – Combien de parties de cardinal pair ?

Une question, voisine de la précédente, consiste à dénombrer les parties de E qui sont de cardinal pair. Deux points de vue sont envisagés ci-dessous.

Premier point de vue

On sait que, pour tout k\in\llbracket0,n\rrbracket, le nombre de parties de E de cardinal k est \binom{n}{k}. Par conséquent, le nombre de parties de cardinal pair est :

    \[A_{n}=\binom{n}{0}+\binom{n}{2}+\binom{n}{4}+\cdots+\binom{n}{2p}\]

où 2p désigne le plus grand entier pair et inférieur ou égal à n. Autrement dit :

    \[A_{n}=\sum_{k=0}^{\left\lfloor n/2\right\rfloor }\binom{n}{2k}\]

De la même façon, le nombre de parties de cardinal impair est :

    \[B_{n}=\binom{n}{1}+\binom{n}{3}+\binom{n}{5}+\cdots+\binom{n}{2q+1}\]

où 2q+1 désigne le plus grand entier impair et inférieur ou égal à n. Autrement dit :

    \[B_{n}=\sum_{k=0}^{\left\lfloor (n-1)/2\right\rfloor }\binom{n}{2k+1}\]

Il ne « reste plus qu’à » calculer ces deux sommes, ce qui va pour l’essentiel reposer sur la formule du binôme. En effet :

    \[A_{n}+B_{n}=\sum_{k=0}^{n}\binom{n}{k}=\left(1+1\right)^{n}=2^{n}\qquad\left(\spadesuit\right)\]

Mais cette seule relation ne suffit pas pour calculer les deux entiers A_{n} et B_{n}. Il nous en faut une seconde ! La voici :

    \[A_{n}-B_{n}=\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}=\left(1-1\right)^{n}\qquad\left(\clubsuit\right)\]

Et là : attention ! Pour affirmer que \left(1-1\right)^{n}=0, encore faut-il supposer que n\geqslant1 (car pour n=0, cette expression vaut 1).

En ajoutant et en retranchant membre à membre les égalités \left(\spadesuit\right) et \left(\clubsuit\right), on obtient :

    \[\forall n\in\mathbb{N}^{\star},\:A_{n}=B_{n}=2^{n-1}\]

Remarque

Il existe donc, dans tout ensemble fini et non vide, autant de parties de cardinal pair que de parties de cardinal impair.

Quant au cas où n=0, il se traite à part. Et il est clair que A_{0}=1 (l’ensemble vide est la seule partie de cardinal pair de l’ensemble vide) et B_{0}=0 (il n’existe, dans l’ensemble vide, aucune partie de cardinal impair !).

Je vous propose de réfléchir à la question suivante :

Exercice

En vous inspirant des calculs ci-dessus, sauriez-vous trouver une formule pour le nombre de parties dont le cardinal est multiple de 3 ?

Tiens ! Je pense que cette question mérite d’être posée dans la rubrique Challenges.

Hop , c’est fait !

🙂

Second point de vue

Notons \mathcal{P}^{0}\left(E\right) l’ensemble de parties de E qui sont de cardinal pair.

De même, notons \mathcal{P}^{1}\left(E\right) l’ensemble de parties de E qui sont de cardinal impair.

D’une part (union disjointe) :

    \[\mathcal{P}^{0}\left(E\right)\sqcup\mathcal{P}^{1}\left(E\right)=\mathcal{P}\left(E\right)\]

et donc (cf. définitions de A_{n} et B_{n} données plus haut) :

    \[A_{n}+B_{n}=2^{n}\]

D’autre part, on va montrer [ cf. détail ci-dessous ] que si n\geqslant1, alors il existe une bijection de \mathcal{P}^{0}\left(E\right) vers \mathcal{P}^{1}\left(E\right), ce qui entraînera :

    \[A_{n}=B_{n}\]

Et de la combinaison de ces deux relations, on déduira aussitôt (comme on l’a fait dans le premier point de vue) que :

    \[A_{n}=B_{n}=2^{n-1}\]

Il reste donc à expliquer cette histoire de bijection…

Observation-Clef

Si l’on crée un ensemble Y en adjoignant à un ensemble fini X un nouvel élément, ou bien en retirant un élément à X, alors les cardinaux de X et de Y sont de parités contraires.

Après avoir fixé un élément a de E (ce qui sous-entend évidemment que E n’est pas vide), on peut considérer l’application :

    \[\theta:\mathcal{P}\left(E\right)\rightarrow\mathcal{P}\left(E\right),\thinspace X\mapsto\left\{ \begin{array}{cc}X\cup\left\{ a\right\} & \text{si }a\notin X\\\\X-\left\{ a\right\} & \text{si }a\in X\end{array}\right.\]

Il est clair (selon l’observation-clef) que \theta induit d’une part une application \alpha:\mathcal{P}^{0}\left(E\right)\rightarrow\mathcal{P}^{1}\left(E\right) ainsi qu’une application \beta:\mathcal{P}^{1}\left(E\right)\rightarrow\mathcal{P}^{0}\left(E\right).

On constate que :

    \[\alpha\circ\beta=id_{\mathcal{P}^{1}\left(E\right)}\qquad\text{et}\qquad\beta\circ\alpha=id_{\mathcal{P}^{0}\left(E\right)}\]

ce qui prouve (notamment) le caractère bijectif de \alpha.

3 – Couples de parties disjointes

Autre question classique, toujours en rapport étroit avec ce qui précède : combien peut-on former de couples \left(X,Y\right) de parties de E vérifiant X\cap Y=\emptyset ?

Comme toujours avec ce genre de questions, les techniques générales de combinatoire, vont nous être d’un grand secours. Pour commencer, on va classer les couples en question selon le cardinal de X.

Notons donc :

    \[C=\left\{ \left(X,Y\right)\in\mathcal{P}\left(E\right)^{2};\thinspace X\cap Y=\emptyset\right\}\]

et

    \[C_{k}=\left\{ \left(X,Y\right)\in\mathcal{P}_{k}\left(E\right)\times\mathcal{P}\left(E\right);\thinspace X\cap Y=\emptyset\right\}\]

de sorte que :

    \[C=\bigsqcup_{k=0}^{n}C_{k}\]

Notons aussi, pour tout \left(k,X\right)\in\llbracket0,n\rrbracket\times\mathcal{P}_{k}\left(E\right) :

    \[C_{k}\left(X\right)=\left\{ \left(X,Y\right);\thinspace Y\in\mathcal{P}\left(E\right)\text{ et }X\cap Y=\emptyset\right\}\]

Dire qu’une partie Y de E ne rencontre pas X revient à dire qu’elle est incluse dans le complémentaire de X. Ainsi :

    \[C_{k}\left(X\right)=\left\{ \left(X,Y\right);\thinspace Y\in\mathcal{P}\left(E-X\right)\right\}\]

Ce dernier ensemble est en bijection avec \mathcal{P}\left(E-X\right), donc \text{card}\left(C_{k}\left(X\right)\right)=2^{n-k}. Et comme :

    \[C_{k}=\bigsqcup_{X\in\mathcal{P}_{k}\left(E\right)}C_{k}\left(X\right)\]

il en résulte que :

    \[\text{card}\left(C_{k}\right)=\sum_{X\in\mathcal{P}_{k}\left(E\right)}\text{card}\left(C_{k}\left(X\right)\right)=\binom{n}{k}2^{n-k}\]

d’où :

    \[\text{card}\left(C\right)=\sum_{k=0}^{n}\binom{n}{k}2^{n-k}\]

et finalement, d’après la formule du binôme :

    \[\boxed{\text{card}\left(C\right)=3^{n}}\]

Afin, d’illustrer ce résultat, voici lorsque n=3 la liste des 3^{3}=27 couples de parties disjointes d’un ensemble à trois éléments.

Si E=\left\{ a,b,c\right\} , alors :

    \[C=\left\{ \begin{array}{ccc}\left(\emptyset,\emptyset\right); & \left(\emptyset,\left\{ a\right\} \right); & \left(\emptyset,\left\{ b\right\} \right);\\\left(\emptyset,\left\{ c\right\} \right); & \left(\emptyset,\left\{ a,b\right\} \right); & \left(\emptyset,\left\{ a,c\right\} \right);\\\left(\emptyset,\left\{ b,c\right\} \right); & \left(\emptyset,\left\{ a,b,c\right\} \right); & \left(\left\{ a\right\} ,\emptyset\right);\\\left(\left\{ a\right\} ,\left\{ b\right\} \right); & \left(\left\{ a\right\} ,\left\{ c\right\} \right); & \left(\left\{ a\right\} ,\left\{ b,c\right\} \right);\\\left(\left\{ b\right\} ,\emptyset\right); & \left(\left\{ b\right\} ,\left\{ a\right\} \right); & \left(\left\{ b\right\} ,\left\{ c\right\} \right);\\\left(\left\{ b\right\} ,\left\{ a,c\right\} \right); & \left(\left\{ c\right\} ,\emptyset\right); & \left(\left\{ c\right\} ,\left\{ a\right\} \right);\\\left(\left\{ c\right\} ,\left\{ b\right\} \right); & \left(\left\{ c\right\} ,\left\{ a,b\right\} \right); & \left(\left\{ a,b\right\} ,\emptyset\right);\\\left(\left\{ a,b\right\} ,\left\{ c\right\} \right); & \left(\left\{ a,c\right\} ,\emptyset\right); & \left(\left\{ a,c\right\} ,\left\{ b\right\} \right);\\\left(\left\{ b,c\right\} ,\emptyset\right); & \left(\left\{ b,c\right\} ,\left\{ a\right\} \right); & \left(\left\{ a,b,c\right\} ,\emptyset\right)\end{array}\right\}\]

Pfouhh ! Compliqué, celui-là … 😅

4 – Nombre de partitions

Rappelons qu’une partition de E est un ensemble de parties non vides de E, deux à deux disjointes et dont l’union est égale à E (ce qui suppose évidemment que E\neq\emptyset).

Il n’est pas difficile de déduire de ce qui précède le calcul du nombre de partitions en deux parties d’un ensemble E de cardinal n.

En effet, il existe 2\left(2^{n}-1\right)+1 couples de parties disjointes comportant \emptyset, à savoir :

→ les 2^{n}-1 couples du type \left(X,\emptyset\right) avec X\neq\emptyset
→ les 2^{n}-1 couples du type \left(\emptyset,X\right) avec X\neq\emptyset
→ le couple \left(\emptyset,\emptyset\right)

Par différence, il nous reste 3^{n}-2\left(2^{n}-1\right)-1 couples de parties non vides et disjointes. Comme aucun de ces couples n’est de la forme \left(X,X\right), il suffit de diviser ce nombre par 2 pour obtenir ce qu’on cherche : il faut bien voir, en effet, qu’un couple est une structure ordonnée tandis qu’une partition ne l’est pas (une partition est un ensemble) : par exemple, les couples \left(\left\{ a\right\} ,\left\{ b,c\right\} \right) et \left(\left\{ b,c\right\} ,\left\{ a\right\} \right) sont distinctes, mais \left\{ \left\{ a\right\} ,\left\{ b,c\right\} \right\} et \left\{ \left\{ b,c\right\} ,\left\{ a\right\} \right\} représentent une seule et même partition de \left\{ a,b,c\right\} .

On conclut ainsi :

    \[\boxed{\text{Il existe }\frac{3^{n}-1}{2}-2^{n}+1\text{ partitions de }E\text{ en deux parties}}\]


Et quel est le nombre total de partitions de E ?

Cette question est plus délicate. Et annonçons toute de suite la couleur : nous n’obtiendrons pas de formule explicite pour le nombre B_{n} de partitions d’un ensemble de cardinal n (cet entier B_{n} est appelé : n-ème nombre de Bell). Nous devrons nous contenter d’une formule de récurrence…

Fixons un élément a\in E et mettons de côté la partition réduite à \left\{ E\right\} . Toutes les autres partitions se composent d’au moins 2 parties, dont l’une exactement contient a. Notons F cette partie et posons \text{card}\left(F\right)=k+1, avec 0\leqslant k\leqslant n-1. Pour chaque entier k\in\llbracket0,n-1\rrbracket
donné, on peut choisir F de \binom{n}{k} façons (c’est une quelconque partie de E, de cardinal k+1 et qui contient a). Et pour chaque tel choix, il faut encore compléter la partition, ce qui peut se faire de B_{n-k} façons (puisque cela revient à partitioner E-F, qui est de cardinal \left(n+1\right)-\left(k+1\right)=n-k).

Au total :

    \[B_{n+1}=1+\sum_{k=0}^{n-1}\binom{n}{k}B_{n-k}\]

Ré-indexons en posant j=n-k. Il vient :

    \[B_{n+1}=1+\sum_{j=1}^{n}\binom{n}{n-j}B_{j}=1+\sum_{j=1}^{n}\binom{n}{j}B_{j}\]

Si l’on pose B_{0}=1 par convention, cette formule de récurrence (forte) prend la forme :

    \[\boxed{\forall n\in\mathbb{N},\:B_{n+1}=\sum_{j=0}^{n}\binom{n}{j}B_{j}}\]

Avec ce joli résultat en poche, on peut calculer la valeur de B_{n} pour de petites valeurs de n :

Voici une illustration montrant les 5 partitions d’un ensemble à 3 éléments :

Et en voici une autre, montrant les 15 partitions d’un ensemble à 4 éléments :

Tout un tas de questions jaillissent ici ! Peut-on calculer les B_{n} plus efficacement que par l’intermédiaire de la formule de récurrence encadrée plus haut ? Peut-on décrire le comportement asymptotique de la suite des nombres de Bell ? Peut-on la relier, ou au moins la comparer à une autre suite similaire (comme celle des nombres de Catalan) ?

Peut-être dans un prochain article, qui sait ?

Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article
    
Étiquettes : , , , , , , , , , , , , , , , , ,

Laisser un commentaire