
Dans cet article, je vous propose de voir comment un même artifice technique, emprunté à la théorie des groupes finis, permet d’établir les trois résultats suivants (![]() désigne un nombre premier) :
désigne un nombre premier) :
Théorème 1 (Wilson)
![]()
Théorème 2 (Fermat)
![]()
Théorème 3 (Euler)
![]()
Ce dernier énoncé est un cas particulier du critère d’Euler.
Avant d’entrer dans le vif du sujet, précisons les notations et rappelons quelques résultats.
Section 1 – Rapide survol de l’anneau  et du corps
et du corps 
Etant donné un entier ![]() la notation
la notation ![]() indique que l’entier
indique que l’entier ![]() est congru à l’entier
est congru à l’entier ![]() modulo
modulo ![]() ce qui signifie que
ce qui signifie que ![]() est un diviseur de
est un diviseur de ![]()
La relation de congruence modulo ![]() est une relation d’équivalence (réflexive, symétrique et transitive) dans
est une relation d’équivalence (réflexive, symétrique et transitive) dans ![]()
La classe d’équivalence de ![]() peut être notée
peut être notée ![]() (notation commode, mais ambigüe puisqu’elle n’indique pas quel est l’entier
(notation commode, mais ambigüe puisqu’elle n’indique pas quel est l’entier ![]() sous-jacent).
sous-jacent).
L’ensemble des classes d’équivalence, noté ![]() comporte
comporte ![]() éléments (à savoir les
éléments (à savoir les ![]() pour
pour ![]() tel que
tel que ![]()
On définit deux opérations (notées ![]() et
et ![]() dans
dans ![]() en posant, pour tout
en posant, pour tout ![]() :
:
![]()
On s’assure de la validité de ces définitions en vérifiant que ![]() et
et ![]() ne dépendent pas des entiers
ne dépendent pas des entiers ![]() et
et ![]() choisis pour représenter ces classes.
choisis pour représenter ces classes.
Muni de ces deux opérations, l’ensemble ![]() devient un anneau commutatif, qui n’est intègre que si
devient un anneau commutatif, qui n’est intègre que si ![]() est premier et qui, dans ce cas, est même un corps (tout élément autre que la classe nulle est inversible).
est premier et qui, dans ce cas, est même un corps (tout élément autre que la classe nulle est inversible).
Lorsque ![]() est premier, on note
est premier, on note ![]() pour
pour ![]() (« corps » se dit « field » en anglais, d’où le
(« corps » se dit « field » en anglais, d’où le ![]()
Section 2 – Factorielle d’un groupe abélien fini
Soit ![]() un groupe abélien fini (l’opération en vigueur dans
un groupe abélien fini (l’opération en vigueur dans ![]() est notée multiplicativement).
est notée multiplicativement).
Je propose de nommer « factorielle de ![]() » et de noter
» et de noter ![]() le produit de tous les éléments de ce groupe.
le produit de tous les éléments de ce groupe.
Ainsi, en notant ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{G!=\prod_{k=1}^{n}a_{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f0cb36e42221e9e94b7310bff572596_l3.png)
ATTENTION …
La notation ![]() n’est pas standard (vous ne la trouverez sans doute pas ailleurs que dans cette note). Elle est cohérente en raison de l’hypothèse de commutativité : peu importe l’ordre dans lequel les éléments de
n’est pas standard (vous ne la trouverez sans doute pas ailleurs que dans cette note). Elle est cohérente en raison de l’hypothèse de commutativité : peu importe l’ordre dans lequel les éléments de ![]() sont énumérés.
sont énumérés.

Signalons aussi que c’est l’associativité du produit dans ![]() qui, fondamentalement, permet d’utiliser la notation
qui, fondamentalement, permet d’utiliser la notation ![]() En effet, sans associativité, l’écriture
En effet, sans associativité, l’écriture ![]() n’aurait aucun sens, puisque différents parenthésages pourraient conduire – a priori – à des produits différents.
n’aurait aucun sens, puisque différents parenthésages pourraient conduire – a priori – à des produits différents.
Considérons par exemple le groupe ![]() des racines
des racines ![]() èmes de l’unité.
èmes de l’unité.
Proposition 1
Pour tout ![]() :
:
![]()
En effet, par définition :
![Rendered by QuickLaTeX.com \[\left[\mathbb{U}_{n}\right]!=\prod_{k=0}^{n-1}e^{2ik\pi/n}=\exp\left(\frac{2i\pi}{n}\sum_{k=0}^{n-1}k\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6650f9dfbcd53f11f772595b40dbac0e_l3.png)
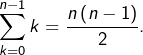 Par conséquent :
Par conséquent : ![]()
![]()
Plus généralement :
Proposition 1 Bis
Soit ![]() groupe cyclique de cardinal
groupe cyclique de cardinal ![]() et d’élément neutre
et d’élément neutre ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \[G!=\left\{ \begin{array}{cc}e & \text{ si }n\text{ est impair}\\\\\epsilon & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-19c271fb21b3ec00650955e945bc6890_l3.png)
Deux groupes cycliques de même cardinal étant isomorphes, on peut se contenter d’invoquer la proposition précédente, mais je trouve éclairant de procéder de manière « directe ».
Les solutions dans ![]() de l’équation
de l’équation ![]() sont, d’une part l’élément neutre et, d’autre part, les éventuels éléments d’ordre 2. Or, dans un groupe fini de cardinal
sont, d’une part l’élément neutre et, d’autre part, les éventuels éléments d’ordre 2. Or, dans un groupe fini de cardinal ![]() l’ordre de tout élément divise
l’ordre de tout élément divise ![]() De plus, si le groupe est cyclique, alors pour tout diviseur
De plus, si le groupe est cyclique, alors pour tout diviseur ![]() de
de ![]() les éléments d’ordre
les éléments d’ordre ![]() sont les générateurs de l’unique sous-groupe de cardinal
sont les générateurs de l’unique sous-groupe de cardinal ![]() (et ces éléments sont au nombre de
(et ces éléments sont au nombre de ![]() où
où ![]() est l’indicatrice d’Euler). On voit en particulier que :
est l’indicatrice d’Euler). On voit en particulier que :
- Cas 1 – Si
 est impair, alors
est impair, alors 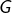 ne possède aucun élément d’ordre 2
ne possède aucun élément d’ordre 2 - Cas 2 – Si
 est pair, alors
est pair, alors 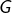 possède un unique élément d’ordre 2
possède un unique élément d’ordre 2
Considérons maintenant le produit qui définit ![]() et plaçons-nous, tour à tour, dans chacun de ces deux cas.
et plaçons-nous, tour à tour, dans chacun de ces deux cas.
Dans le premier cas, en mettant à part le neutre, il reste le produit d’un nombre pair d’éléments, que l’on peut apparier (chacun avec son inverse) et au final :
![]()
Dans le second cas, on isole ![]() et
et ![]() du produit et l’on procède de même (regroupement par paires de tous les éléments restants, chacun avec son inverse), ce qui conduit cette fois à :
du produit et l’on procède de même (regroupement par paires de tous les éléments restants, chacun avec son inverse), ce qui conduit cette fois à :
![]()
Question
Que reste-t-il de ce résultat pour des groupes abéliens finis plus généraux (c’est-à-dire : non cycliques) ?
La proposition ci-dessous apporte une réponse …
Proposition 2
Pour tout groupe abélien fini ![]() d’élément neutre
d’élément neutre ![]() :
:
![]()
En effet, l’application ![]() est une involution. Par conséquent :
est une involution. Par conséquent :
![Rendered by QuickLaTeX.com \[\left[G!\right]^{2}=\left(\prod_{a\in G}a\right)^{2}=\left(\prod_{a\in G}a\right)\left(\prod_{a\in G}a^{-1}\right)=\prod_{a\in G}\left(aa^{-1}\right)=e\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-73af58c8bd61c98e2a4701408e652822_l3.png)
Ce dernier résultat est présenté ici pour son intérêt propre : dans tout groupe abélien fini, le produit des éléments est soit neutre soit d’ordre 2.
Cela dit, nous n’en aurons pas besoin dans la suite puisque le groupe ![]() que nous allons utiliser est cyclique (et la proposition 1Bis s’appliquera).
que nous allons utiliser est cyclique (et la proposition 1Bis s’appliquera).
Section 3 – Théorème de Wilson
Supposons ![]() premier,
premier, ![]()
Appliquons au groupe ![]() la méthode suivie pour la proposition 1Bis, à ceci près qu’il ne va pas être nécessaire de savoir au préalable que ce groupe est cyclique.
la méthode suivie pour la proposition 1Bis, à ceci près qu’il ne va pas être nécessaire de savoir au préalable que ce groupe est cyclique.
Les solutions dans le corps ![]() de l’équation
de l’équation ![]() sont
sont ![]() et
et ![]() Ces deux classes (qui n’en feraient qu’une pour
Ces deux classes (qui n’en feraient qu’une pour ![]() …) sont donc les deux seuls éléments de
…) sont donc les deux seuls éléments de ![]() qui coïncident avec leur inverse. Les
qui coïncident avec leur inverse. Les ![]() autres éléments vont donc pouvoir être appariés, chacun avec son inverse (noter que
autres éléments vont donc pouvoir être appariés, chacun avec son inverse (noter que ![]() est pair) ce qui donne :
est pair) ce qui donne :
![Rendered by QuickLaTeX.com \[\overline{\left(p-1\right)!}=\prod_{k=1}^{p-1}\overline{k}=\overline{1}\times\overline{p-1}\times\prod_{k=2}^{p-2}\overline{k}=\overline{p-1}=-\overline{1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c96e96e243a602a4d18e691635a2b2f_l3.png)
(![]() )
) ![]()
Le théorème de Wilson est démontré.
Remarque
La réciproque du théorème de Wilson est vraie.
En effet, supposons qu’un entier ![]() vérifie
vérifie ![]() et imaginons un instant que
et imaginons un instant que ![]() ne soit pas premier. Alors il existerait un entier
ne soit pas premier. Alors il existerait un entier ![]() tel que
tel que ![]() et
et ![]() De
De ![]() on déduit que
on déduit que ![]() et de
et de ![]() on déduit que
on déduit que ![]() et donc, par différence,
et donc, par différence, ![]() ce qui est absurde.
ce qui est absurde.
Ainsi, la congruence ![]() caractérise les nombres premiers. Bien entendu, ceci constitue un piètre test de primalité, car pour
caractérise les nombres premiers. Bien entendu, ceci constitue un piètre test de primalité, car pour ![]() assez grand, il faudrait calculer la factorielle de
assez grand, il faudrait calculer la factorielle de ![]() qui est un entier de taille colossale !
qui est un entier de taille colossale !
Section 4 – Petit théorème de Fermat
Théorème
Si ![]() alors pour tout
alors pour tout ![]() :
:
![]()
Ce résultat se démontre classiquement par récurrence (sur ![]() bien sûr). La preuve repose de façon cruciale le fait que le coefficient binomial
bien sûr). La preuve repose de façon cruciale le fait que le coefficient binomial ![]() est multiple de
est multiple de ![]() pour tout
pour tout ![]() tel que
tel que ![]()
Si cette preuve vous intéresse, je vous invite à la lire en annexe.
Voici l’essence de notre démonstration.
Si ![]() est un groupe abélien fini de cardinal
est un groupe abélien fini de cardinal ![]() alors :
alors :
- en notant
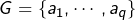
- et en choisissant
 (de sorte que
(de sorte que  pour un certain
pour un certain 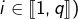
l’application ![]() est une bijection (dont la réciproque est
est une bijection (dont la réciproque est ![]()
Par conséquent :
![Rendered by QuickLaTeX.com \[G!=\prod_{k=1}^{q}a_{k}=\prod_{k=1}^{q}\left(xa_{k}\right)=x^{q}\thinspace G!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0f00e19566b6e36c6c87788b728f67aa_l3.png)
![]()
Remarque
Il découle du théorème de Lagrange (qui fait l’objet de cette vidéo) que dans tout groupe fini de cardinal ![]() (non nécessairement abélien), la puissance
(non nécessairement abélien), la puissance ![]() ème d’un quelconque élément est égale à l’élément neutre. L’intérêt de ce qui précède est d’en apporter une preuve simplifiée dans le cas particulier des groupes abéliens.
ème d’un quelconque élément est égale à l’élément neutre. L’intérêt de ce qui précède est d’en apporter une preuve simplifiée dans le cas particulier des groupes abéliens.
Appliquons ceci à ![]() (ce qui impose
(ce qui impose ![]() et
et ![]() avec
avec ![]() non multiple de
non multiple de ![]() (cette condition garantissant que
(cette condition garantissant que ![]() c’est-à-dire
c’est-à-dire ![]() On obtient :
On obtient :
![]()
![]()
![]()
Section 5 – Est-ce que -1 est un carré modulo p ?
Donnons-nous un nombre premier ![]() et cherchons à quelle condition l’entier
et cherchons à quelle condition l’entier ![]() est un carré modulo
est un carré modulo ![]() c’est-à-dire à quelle condition (sur
c’est-à-dire à quelle condition (sur ![]() il existe un entier
il existe un entier ![]() tel que :
tel que :
![]()
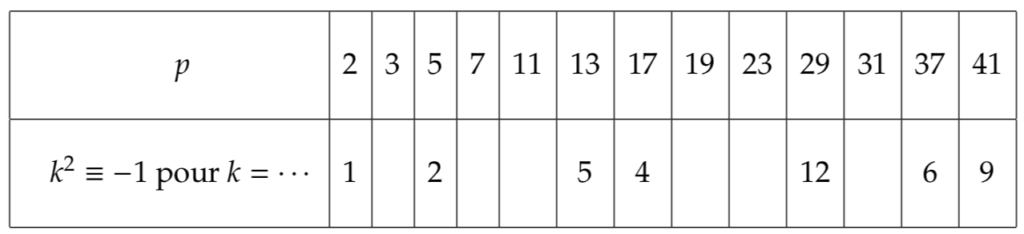
Lorsqu’une case de la seconde ligne de ce tableau est remplie, elle indique l’une des deux racines carrées de ![]() modulo
modulo ![]() Par exemple :
Par exemple :
![]()
Par exemple, ![]() n’est pas un carré modulo
n’est pas un carré modulo ![]() les seuls carrés non nuls étant
les seuls carrés non nuls étant ![]()
![]()
![]()
Conjecture
Il semblerait que, outre ![]() les seuls nombres premiers
les seuls nombres premiers ![]() pour lesquels -1 est un carré modulo
pour lesquels -1 est un carré modulo ![]() soient ceux congrus à 1 modulo 4.
soient ceux congrus à 1 modulo 4.
C’est ce que nous allons maintenant établir.
➣ Dans un sens …
Si ![]() est un carré modulo
est un carré modulo ![]() (avec
(avec ![]() c’est qu’il existe
c’est qu’il existe ![]() vérifiant :
vérifiant :
![]()
Autrement dit : ![]()
➣ Dans l’autre sens …
Supposons que ![]()
On va considérer le produit des éléments de ![]() et regrouper chaque facteur avec son opposé :
et regrouper chaque facteur avec son opposé :
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\prod_{k=1}^{p-1}k & = \prod_{k=1}^{\left(p-1\right)/2}k\left(p-k\right)\\& \equiv \left(-1\right)^{\left(p-1\right)/2}\prod_{k=1}^{\left(p-1\right)/2}k^{2}\\& = \left(-1\right)^{\left(p-1\right)/2}\left[\left(\frac{p-1}{2}\right)!\right]^{2}\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8a04c197f854e0a9584ff22732173442_l3.png)
![]()
![]()
Section 6 – En guise de conclusion
Nous avons regroupé trois propriétés d’arithmétique modulaire :
[1] – le théorème de Wilson
[2] – le petit théorème de Fermat
[3] – un cas particulier du critère d’Euler
- Pour [1], on regroupe chaque facteur (autre que
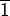 et
et 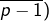 avec son inverse (dans le groupe
avec son inverse (dans le groupe 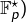
- Pour [2], on multiplie chaque facteur par un même élément de
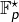 (ce qui n’altère pas le produit)
(ce qui n’altère pas le produit) - Pour [3], on regroupe chaque facteur avec son opposé (dans l’anneau
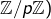
Annexe – Le petit Fermat par récurrence
On fixe un nombre premier ![]() et l’on prouve, par récurrence, que pour tout
et l’on prouve, par récurrence, que pour tout ![]() :
:
![]()
Supposons-la vraie pour un certain ![]() alors d’après la formule du binôme :
alors d’après la formule du binôme :
![Rendered by QuickLaTeX.com \[\left(n+1\right)^{p}=\sum_{k=0}^{p}\binom{p}{k}n^{k}=n^{p}+1+\sum_{k=1}^{p-1}\binom{p}{k}n^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-70cc0a49bd8a3373b3f9cfd8cb32d145_l3.png)
![Rendered by QuickLaTeX.com \[\left(n+1\right)^{p}\equiv n+1+\sum_{k=1}^{p-1}\binom{p}{k}n^{k}\pmod{p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1561737ca150510d476b9fede7336e24_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{p-1}\binom{p}{k}n^{k}\equiv0\pmod{p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d41910223483b062629e87b500c4b770_l3.png)
Lemme
Pour tout entier ![]() tel que
tel que ![]() :
:
![]()
On commence par appliquer la formule du pion (voir cet article) :
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
