
Dans ce qui suit, je vais essayer de vous prouver que l’égalité 64 = 65 est vraie. Si !
Sans doute faudra-t-il que je sois extrêmement convaincant, car je sens déjà une légère réticence de votre part 🙂
Pour que l’expérience soit amusante, il faudra que vous jouiez le jeu : l’air de rien, je vais fatalement affirmer quelque chose de faux dans le fil de ma « démonstration », mais vous devrez être vigilant(e) et tâcher de détecter ce qui ne va pas.
Une dernière chose avant de commencer : munissez-vous d’une feuille de papier quadrillé, d’une règle, d’un crayon et d’une paire de ciseaux.
1 – Préparatifs
Vous allez dessiner deux rectangles, l’un de format 5 ![]() 8 et l’autre de format 3
8 et l’autre de format 3 ![]() 8.
8.
Pour le premier, faites apparaître en pointillés un segment de droite, de manière à partager ce rectangle en deux trapèzes superposables, de hauteur 5 et dont les bases mesurent respectivement 3 et 5, comme indiqué sur la figure ci-dessous.
Pour le second, tracez simplement une diagonale en pointillés.
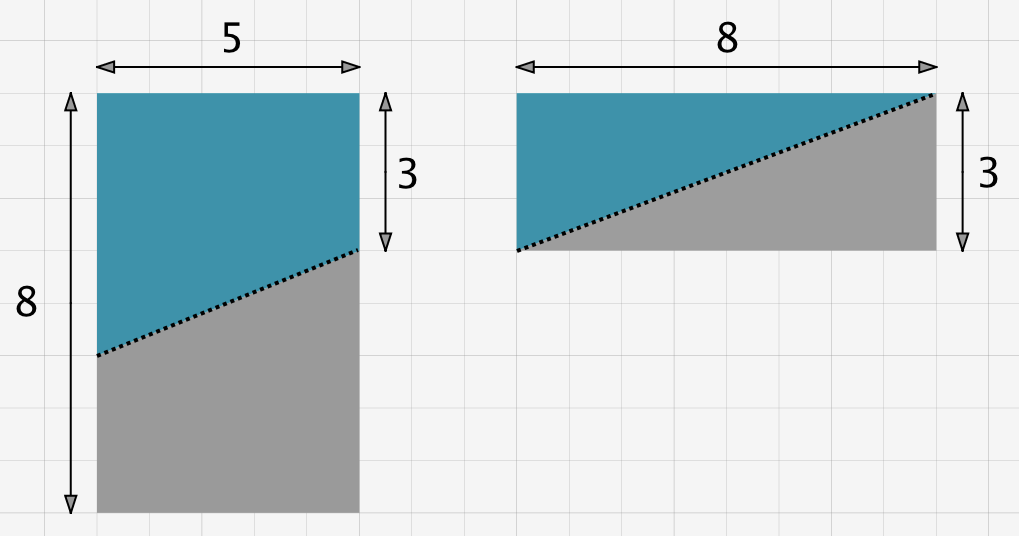
Ensuite, découpez (selon les pointillés) pour obtenir quatre figures : deux triangles rectangles et deux trapèzes.
Section 2
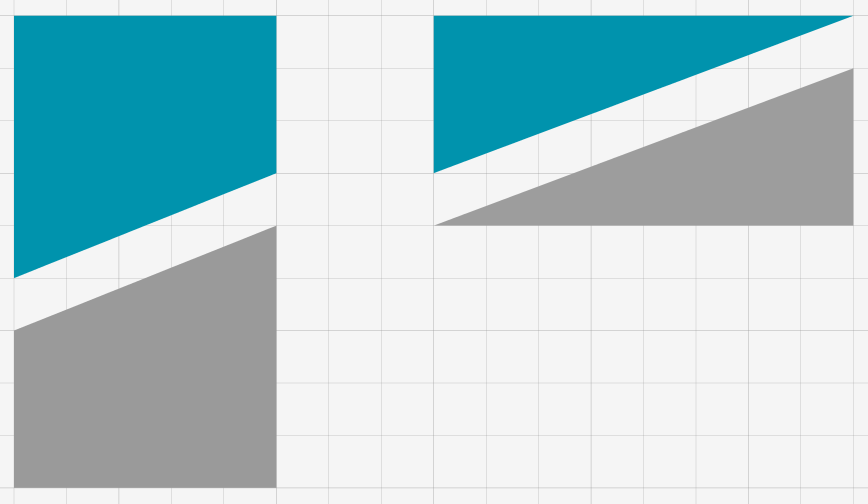
Vous pouvez maintenant déplacer librement ces quatre figures sur la table …
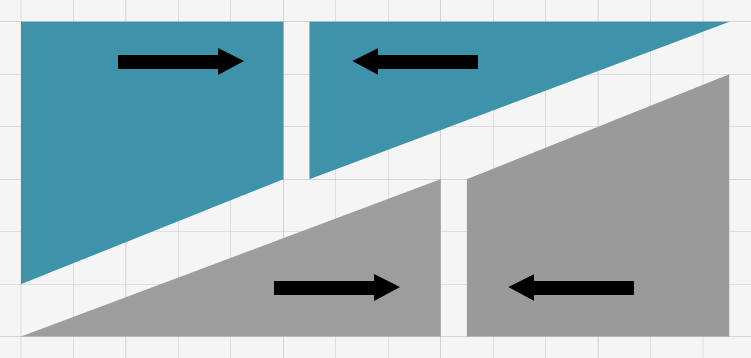
… et les agencer de manière à former deux grands triangles rectangles, dont les côtés de l’angle droit mesurent 5 et 13 :

En accolant les hypoténuses de ces deux triangles rectangles, vous allez former un grand rectangle d’aire ![]() (l’unité choisie pour mesurer les aires est tout naturellement le carreau).
(l’unité choisie pour mesurer les aires est tout naturellement le carreau).
Pourtant, nous sommes initialement partis de deux rectangles plus petits, l’un d’aire ![]() et l’autre d’aire
et l’autre d’aire ![]() ce qui représente un total de
ce qui représente un total de ![]()
Comme l’aire n’a pas varié en cours de route, nous concluons que 64 = 65.
Voilà, voilà. Vous en pensez quoi ?
Ne lisez pas trop vite la suite !…
… à moins que vous ne soyez certain(e) d’avoir identifié une affirmation fausse dans ce qui précède.
3 – Que s’est-il passé ?
Si l’on regarde de près la configuration précédente, on observe ceci (et avec un ordinateur, cela a toutes les chances d’être plus facile à voir qu’avec des morceaux de papier …) :
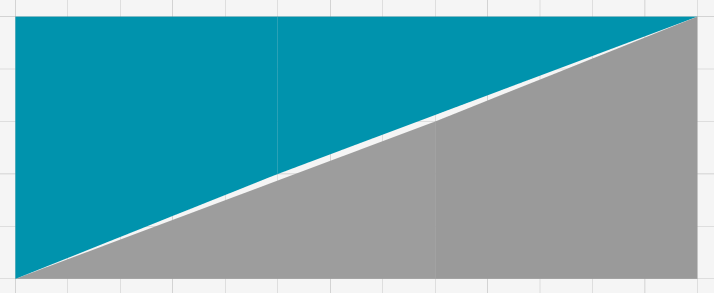
Il y a un vide entre les hypoténuses des deux « triangles »… !
Tout s’explique : ce ne sont pas véritablement des triangles ! Pour chacun d’eux, la soi-disante hypoténuse est en réalité formée de deux segments qui ne sont pas correctement alignés (ou, si vous préférez, ces deux segments n’ont pas la même pente : l’un a pour pente 2/5 = 0,4 et l’autre 3/8 = 0,375).
Clairement, l’aire de la zone très fine qui sépare les deux pseudo-triangles est exactement égale à 1 carreau : c’est précisément ce qui manque à 64 ( = l’aire de l’union des quatre figures) pour obtenir 65 ( = l’aire que devrait posséder ce grand rectangle s’il ne lui manquait rien).
Il ne vous reste plus qu’à faire le coup à vos amis : si vous vous y prenez bien, il tomberont (comme vous ?) dans le panneau … et chercheront peut-être l’erreur là où elle n’est pas.
4 – Encore mieux !
Si votre coup de ciseaux était suffisamment précis, il se peut que vous ayez découvert la supercherie au moment où l’on approche les deux pseudo-triangles l’un de l’autre.
Pour rendre le tour de passe-passe vraiment bluffant, il suffit de remplacer les valeurs 3, 5 et 8 précédemment utilisées par des valeurs plus grandes, convenablement choisies, par exemple 8, 13 et 21.
Bien entendu, les figures doivent pouvoir tenir sur la feuille… il est donc probable que vous ayez à choisir un quadrillage plus fin (j’ai vérifié : une feuille à petits carreaux fait très bien l’affaire).
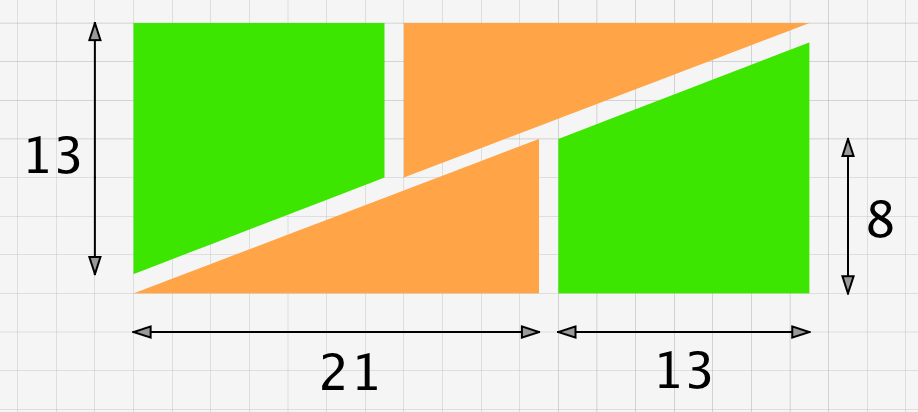
Cette fois, lorsque vous accolerez les deux grands triangles rectangles par leur hypoténuse, l’espace intermédiaire sera parfaitement invisible… et l’illusion sera donc parfaite !
En réalisant le tour à l’identique, vous parviendrez à la conclusion paradoxale suivante : 441 = 442.
Voici deux photos qui montrent ce que ça peut donner :


Il est normal que ce choix de 8, 13 et 21 améliore la qualité de l’illusion, puisqu’une erreur relative de 1 sur 442 est nettement plus difficile à repérer qu’une erreur relative de 1 sur 65.
On voit bien qu’il y a des imperfections sur les photos, mais on sera sans doute tenté de penser qu’elles proviennent d’un découpage ou d’un positionnement imprécis (ou des deux à la fois), avant d’imaginer une autre raison, plus profonde. C’est l’intérêt de faire la manip avec du papier et une paire de ciseaux : on trompe l’ennemi plus facilement qu’avec un écran d’ordinateur 😉
5 – Intermède italien
Que vous évoquent ces nombres entiers : 3, 5, 8, 13, 21 ?
Vous aurez peut-être reconnu des termes consécutifs de la célèbre suite de Fibonacci.
Mais si cette notion ne vous est pas familière, pas de panique ! On explique tout …
Notons ![]() (lire : « F indice n ») l’entier défini de la manière suivante :
(lire : « F indice n ») l’entier défini de la manière suivante :
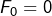
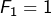
- si
 alors
alors 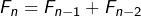
Pour dire les choses de manière moins formelle, on construit une suite de nombres dont les deux premiers termes ![]() et
et ![]() valent respectivement 0 et 1 et dont tous les termes, à partir de
valent respectivement 0 et 1 et dont tous les termes, à partir de ![]() et au-delà, s’obtiennent en faisant la somme des deux termes précédents.
et au-delà, s’obtiennent en faisant la somme des deux termes précédents.
La table ci-dessous renferme les treize premiers termes de cette célèbre suite :

Le nom de cette suite fait référence à un érudit italien dénommé Leonardo Pisano, alias Fibonacci (contraction présumée de « filio Bonacci » : fils de Bonacci), né à Pise en 1175. Fibonacci fait partie de ceux qui ont diffusé les mathématiques arabes (notamment l’utilisation des chiffres indo-arabes et la notation décimale positionnelle) auprès des savants occidentaux de l’époque.
Il a produit, au tout début du XIIème siècle, un traité de calcul et de comptabilité : liber abaci, ce qui signifie en latin « livre des calculs » ou « livre des abaques ». Quelque part dans cet ouvrage, il propose une étude du problème suivant :
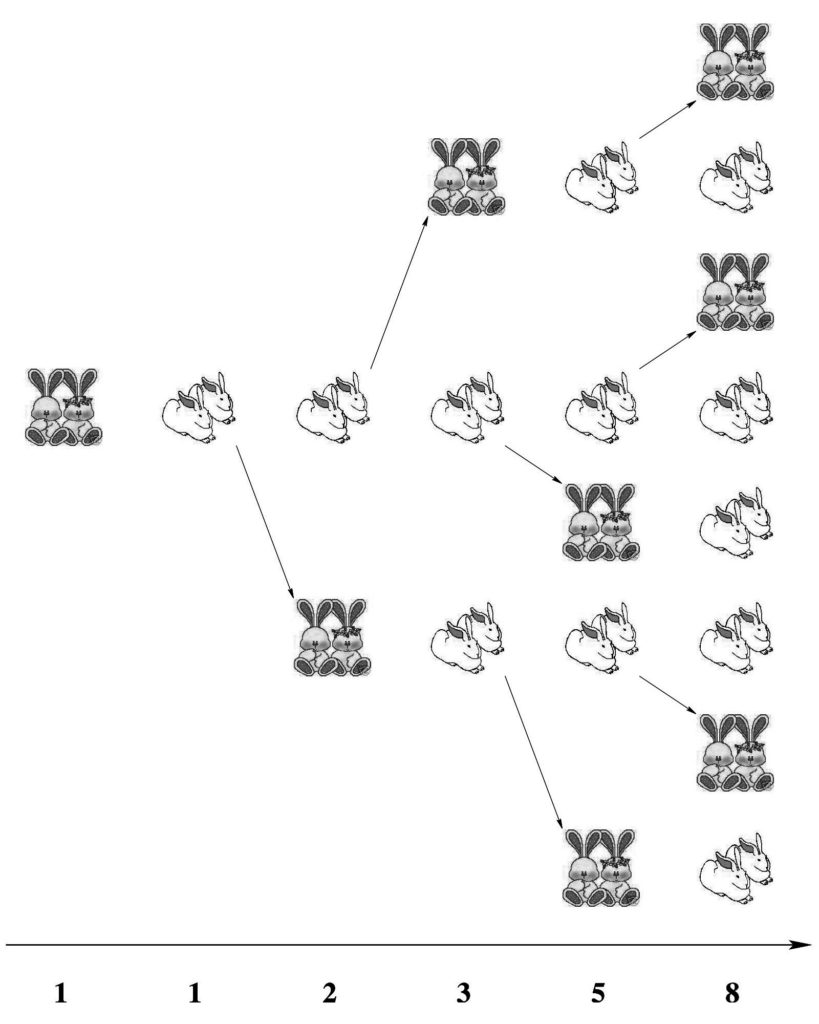
Combien de couples de lapins obtiendrons-nous en fin d’année si, en commençant avec un couple, chaque couple produisait chaque mois un nouveau couple, lequel deviendrait fécond au second mois de son existence ?
Les calculs font apparaître les fameux nombres ![]() définis plus haut…
définis plus haut…
La suite de Fibonacci possède une foule de jolies propriétés, plus ou moins apparentes, plus ou moins connues, plus ou moins faciles à démontrer. Le sujet est si riche qu’une revue canadienne (The Fibonacci Quarterly) lui consacre, chaque trimestre depuis 1963, des articles, des notes et des rubriques questions / réponses !
Un exemple de résultat difficile, démontré en 1964 par John H.E. Cohn, affirme que, parmi tous les termes de la suite de Fibonacci, les seuls carrés parfaits sont 0, 1 et 144. Une preuve est consultable dans le volume 2 de 1964 du Fibonacci Quarterly (référencé ci-dessus et librement accessible en ligne).
6 – Le secret du tour
La propriété suivante des nombres ![]() est en rapport étroit avec notre paradoxe :
est en rapport étroit avec notre paradoxe :
Identité de Cassini
Pour tout entier ![]() :
:
![]()
Preuve (cliquer pour déplier / replier)
Procédons par récurrence…
Pour une initiation à ce type de raisonnement, on pourra consulter l’article :
Qu’est-ce qu’une preuve par récurrence ?
Pour ![]() c’est bien vrai, puisque :
c’est bien vrai, puisque :
![]()
Supposons cette relation vraie pour un certain ![]() Alors :
Alors :
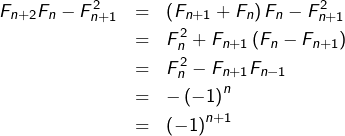
comme souhaité.
Ainsi, le carré d’un quelconque terme de la suite est égal, à une unité près (par excès ou par défaut), au produit du terme précédent par le terme suivant.
Ceci explique pourquoi les nombres 3, 5 et 8 ou encore 8, 13 et 21 ont été choisis dans la construction.
7 – Moralité
On a parfois tendance à justifier une affirmation en s’inspirant d’un dessin ou d’une représentation graphique et en disant « on voit bien sur la figure que … ».
L’exemple que nous venons d’étudier montre bien à quoi on s’expose en laissant le dernier mot à nos sens plutôt qu’à notre capacité à raisonner.
Les mathématiques sont le domaine par excellence où l’on prouve, où l’on démontre véritablement des résultats d’une manière à la fois absolue et définitive :
- Absolue car, à l’issue d’une preuve, la validité du résultat établi ne suscite plus le moindre doute.
- Définitive au sens où, dès lors d’un théorème a été démontré, il le restera à jamais !
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
