
« Prime numbers are the most basic objects in mathematics. They also are among the most mysterious, for after centuries of study, the structure of the set of prime numbers is still not well understood. Describing the distribution of primes is at the heart of much mathematics… »
Le principal obstacle à la vulgarisation des idées mathématiques est sans doute l’incroyable empilement de connaissances qui s’impose pour aborder le moindre thème de recherche contemporain.
Un chercheur en biologie cellulaire sera évidemment dans l’impossibilité d’exposer le détail de ses travaux à une personne non-initiée. Mais il pourra sans doute, même de façon imprécise, donner quelques indications sur la nature de ses recherches. Il pourra dire, par exemple : « j’étudie l’impact de l’environnement sur les mécanismes de mutation génétique chez certains mammifères marins » ou encore « je m’intéresse à la possibilité de transférer des gènes d’une espèce végétale vers une autre »…
En mathématiques, l’analogue est en général impossible, car la somme de connaissances préalables qui permettraient de comprendre de quoi il retourne – ne serait-ce que superficiellement – est déjà trop élevée …
On trouve cependant des exceptions, notamment en arithmétique.
L’arithmétique est riche en questions difficiles (voire non résolues pour certaines) dont la formulation est parfaitement accessible au débutant, voire au profane.
Certaines de ces questions concernent les nombres premiers.
Pour information : cette vidéo aborde sensiblement les mêmes thèmes que le présent article.
1 – Qu’est-ce qu’un nombre premier ?
Imaginons une collection d’objets identiques que l’on cherche à disposer en rangées de même longueur, pour obtenir une configuration « rectangulaire », comme dans l’illustration ci-dessous.
Avec 12 objets, on peut former 3 colonnes de 4 objets, ou bien 2 colonnes de 6 ou encore une seule colonne de 12 (bien entendu, on peut aussi réaliser 4 colonnes de 3, ou 6 colonnes de 2 ou encore 12 colonne réduites à un seul objet, mais c’est la même chose !!) :
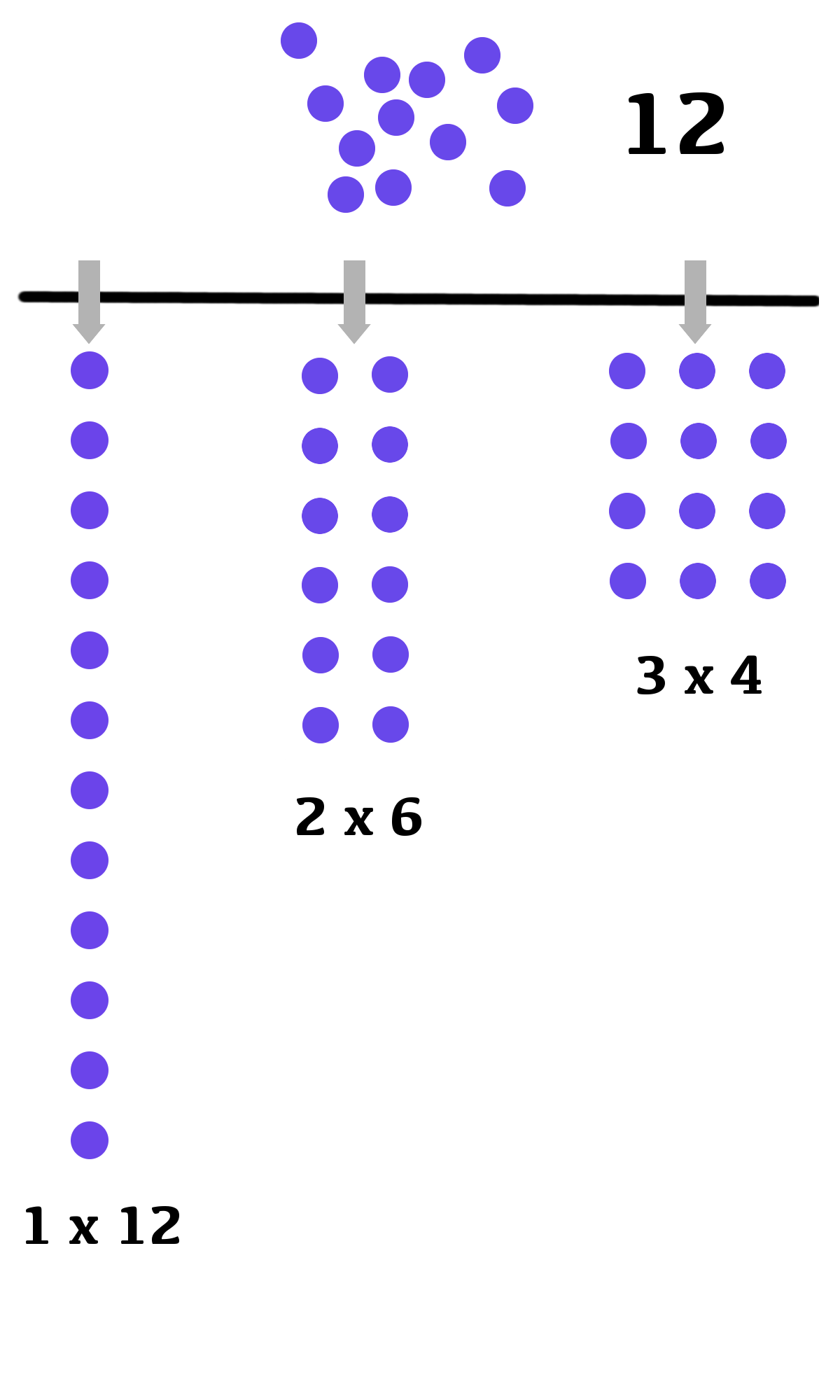
En revanche, si l’on remplace 12 par 13, la seule possibilité consiste en une seule rangée rassemblant les 13 objets. On dit, pour cette raison, que 13 est un nombre premier.
Voici une définition plus « sérieuse » :
Définition d’un nombre premier
Un entier naturel est dit premier, lorsqu’il est supérieur ou égal à 2 et ne possède aucun diviseur, à l’exception de lui-même et de 1. Autre façon de dire la même chose : un entier ![]() est premier lorsqu’il ne possède aucun diviseur « non trivial » (les diviseurs triviaux de
est premier lorsqu’il ne possède aucun diviseur « non trivial » (les diviseurs triviaux de ![]() sont 1 et
sont 1 et ![]() ).
).
Les nombres premiers sont donc, parmi les entiers positifs, ceux qui sont « indécomposables », que l’on ne peut pas scinder en produit d’entiers plus petits. Si l’on osait une comparaison entre l’arithmétique et la chimie, on pourrait dire que les nombres premiers sont aux entiers naturels ce que les corps simples (fer, carbone, hydrogène, azote, oxygène, etc …) sont aux espèces chimiques plus générales (eau, méthane, glucose, acide désoxyribonucléique, etc …).
Remarque
L’entier 1 n’est pas considéré comme premier, bien qu’il ne soit divisible que par 1 et par lui-même ! Ceci peut paraître étonnant, mais le point de vue contraire aurait une fâcheuse conséquence. En effet, le théorème fondamental de l’arithmétique (voir section 3) affirme l’existence et l’unicité de la décomposition en facteurs premiers d’un entier : en acceptant 1 dans l’ensemble des nombres premiers, on perdrait l’unicité de cette décomposition.
2 – Les premiers nombres premiers 🙂
Le plus petit nombre premier est 2. C’est évidemment le seul qui soit pair. Ensuite viennent, dans l’ordre croissant : 3, 5, 7, 11, 13, 17, 19, etc …
Voici la liste des nombre premiers inférieurs à 1000. Il en existe 168 :
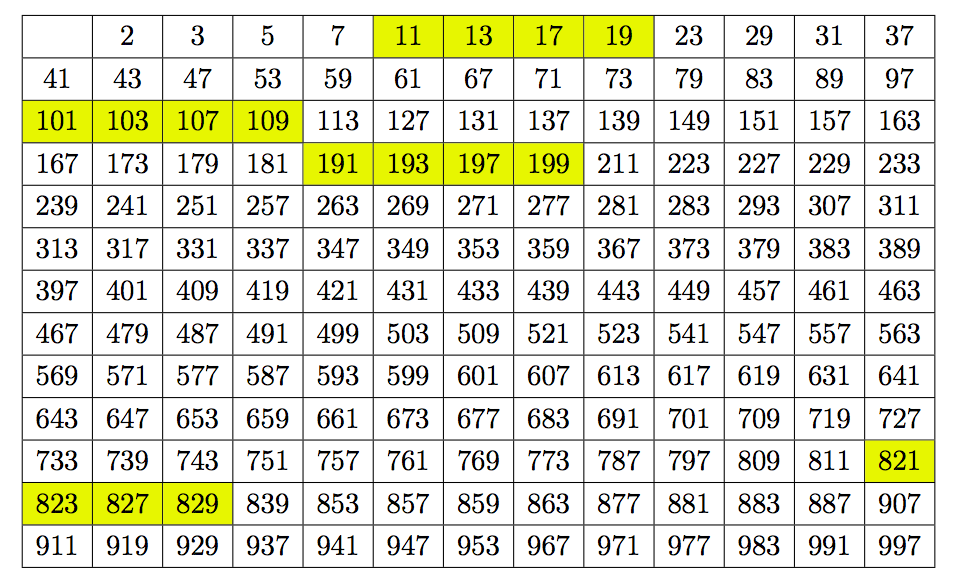
Les cases colorées correspondent à une curiosité : il arrive qu’on trouve quatre nombres premiers un sein d’une même dizaine, c’est-à-dire des entiers de la forme ![]() ,
, ![]() ,
, ![]() et
et ![]() pour un certain
pour un certain ![]() .
.
Ceci ne se produit que quatre fois parmi les entiers inférieurs à 1000 :
- 11, 13, 17, 19
- 101, 103, 107, 109
- 191, 193, 197, 199
- 821, 823, 827, 829
Existe-t-il une infinité de tels quadruplets ?
Une célèbre conjecture de Hardy et Littlewood affirme que oui, mais elle reste à ce jour non prouvée. Noter qu’une confirmation établirait l’existence d’une infinité de nombres premiers jumeaux ! Voir à ce sujet l’article « Qu’est-ce qu’une conjecture en mathématiques ? » ainsi que la dernière section du présent texte, consacrée à quelques conjectures célèbres.
3 – Quelques bons bouquins …
Avant de poursuivre, je vous propose quelques ouvrages de qualité, relatifs aux nombres premiers.
En cliquant sur l’une quelconque des images ci-dessous, vous pourrez commander le livre correspondant sur Amazon.
Je me suis limité à six références, dont une en anglais. Ce sont de très bons livres, que je vous recommande particulièrement.
Le premier livre proposé est une fiction originale qui gravite autour de la conjecture de Goldbach.
4 – Décomposition en produit de facteurs premiers
Proposition
Tout nombre entier ![]() possède au moins un diviseur premier.
possède au moins un diviseur premier.
C’est assez facile à comprendre. En effet, il se peut que ![]() soit lui-même premier, auquel cas un diviseur premier est tout trouvé :
soit lui-même premier, auquel cas un diviseur premier est tout trouvé : ![]() lui-même !
lui-même !
Et sinon, cela signifie que ![]() possède un diviseur non trivial, disons
possède un diviseur non trivial, disons ![]() (avec
(avec ![]() ). On peut appliquer le même argument à l’entier
). On peut appliquer le même argument à l’entier ![]() : soit il est premier, soit il possède un diviseur strictement compris entre 1 et
: soit il est premier, soit il possède un diviseur strictement compris entre 1 et ![]() .
.
On reproduisant ce schéma, on abouti fatalement à un nombre premier, après un certain nombre d’étapes. En effet, si le processus se poursuivait indéfiniment sans jamais déboucher sur un nombre premier, cela donnerait naissance à une suite interminable de nombres entiers positifs, chacun étant strictement inférieur au précédent, ce qui est impossible (car il n’existe pas de suite strictement décroissante d’entiers positifs) !
Voici une présentation rigoureuse de cet argument (voir à ce sujet les sections 8 et 9 de cet article) :
Preuve par récurrence forte (cliquer pour déplier / replier)
Montrons que l’assertion ![]() suivante :
suivante :
il existe un nombre premier qui divise ![]()
est vraie pour tout entier ![]() .
.
- [ Initialisation ] L’assertion
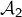 est vraie puisque 2 est premier.
est vraie puisque 2 est premier. - [ Hérédité ] Supposons
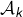 vraie pour tous les entiers
vraie pour tous les entiers 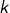 tels que
tels que 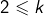 . Si
. Si  est premier, c’est réglé. Et sinon,
est premier, c’est réglé. Et sinon,  admet un diviseur
admet un diviseur 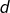 tel que
tel que 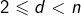 . D’après l’hypothèse de récurrence,
. D’après l’hypothèse de récurrence, 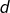 admet un diviseur premier, qui est aussi diviseur de
admet un diviseur premier, qui est aussi diviseur de  .
.
Considérons maintenant un entier ![]() . Divisons
. Divisons ![]() par son plus petit facteur premier et notons
par son plus petit facteur premier et notons ![]() le résultat de cette opération. Clairement,
le résultat de cette opération. Clairement, ![]() et nous pouvons envisager deux possibilités :
et nous pouvons envisager deux possibilités :
- Soit
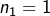 et c’est terminé,
et c’est terminé, - Soit
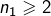 auquel cas on peut recommencer : on divise
auquel cas on peut recommencer : on divise 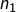 par son plus petit facteur premier, ce qui donne un entier
par son plus petit facteur premier, ce qui donne un entier  et ainsi de suite …
et ainsi de suite …
Lorsque ce processus se termine, ![]() apparaît comme un produit de nombres premiers.
apparaît comme un produit de nombres premiers.
Certains d’entre-eux peuvent être égaux, ce qui nous incite à les regrouper, pour obtenir au final la « décomposition en facteurs premiers » (ou DFP) de ![]() :
:
![]()
Remarque
On a établi ici l’existence de la DFP. Dans cet article, la question de l’unicité (à l’ordre près des facteurs) est laissée de côté. Le lecteur intéressé pourra la trouver par ailleurs.
Le fait que tout entier naturel supérieur ou égal à 2 puisse s’écrire, de manière unique à l’ordre près des facteurs, comme un produit de nombres premiers constitue le Théorème Fondamental de l’Arithmétique.
Exemple
Calculons la DFP de n=728.
- Le plus petit facteur premier (ou PPFP) de 728 est 2 et
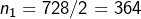
- Le PPFP de 364 est encore 2 et
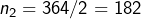
- Le PPFP de 182 est toujours 2 et
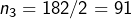
- Le PPFP de 91 est 7 et
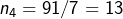
- Enfin, 13 est premier.
Donc :
![]()
![]()
L’exemple ci-dessus se traite sans difficulté. Mais si l’entier ![]() est assez grand, le calcul de son PPFP (et a fortiori de sa DFP) peut demander beaucoup de travail…
est assez grand, le calcul de son PPFP (et a fortiori de sa DFP) peut demander beaucoup de travail…
Et pour des entiers de grande taille (quelques milliers de chiffres décimaux), ce calcul est carrément hors de portée – du moins dans l’état actuel de nos connaissances et avec les outils de calcul électronique dont nous disposons.
Nous allons à présent décrire un petit algorithme qui permet le calcul du PPFP d’un entier ![]() .
.
5 – Calcul du plus petit facteur premier
Etant donné un entier ![]() on va déterminer son plus petit facteur premier, noté
on va déterminer son plus petit facteur premier, noté ![]()
Commençons par une observation-clef, qui nous évitera d’envisager des tests superflus.
Proposition
Si un entier ![]() ne possède aucun diviseur non trivial parmi les entiers inférieurs ou égaux à
ne possède aucun diviseur non trivial parmi les entiers inférieurs ou égaux à ![]() alors
alors ![]() est premier.
est premier.
Preuve (cliquer pour déplier / replier)
On raisonne par l’absurde. Si ![]() est composé (c’est-à-dire non premier), alors
est composé (c’est-à-dire non premier), alors ![]() possède un diviseur
possède un diviseur ![]() tel que
tel que ![]() Vue l’hypothèse, on sait que
Vue l’hypothèse, on sait que ![]() Mais l’entier
Mais l’entier ![]() est aussi un diviseur de
est aussi un diviseur de ![]() strictement compris entre
strictement compris entre ![]() et
et ![]() on a donc pour les mêmes raisons
on a donc pour les mêmes raisons ![]() Il s’ensuit que
Il s’ensuit que ![]()
C’est absurde !
Avec ce résultat en poche, on peut proposer l’algorithme suivant :
Algorithme standard de calcul du PPFP
Etant donné un entier ![]() on calcule
on calcule ![]() comme suit :
comme suit :
➢ Si ![]() est pair, alors
est pair, alors ![]()
➢ Sinon, on parcourt dans l’ordre croissant la liste des entiers impairs de 3 à la « racine carrée entière » de ![]() (càd : le plus grand entier naturel dont le carré est inférieur ou égal à
(càd : le plus grand entier naturel dont le carré est inférieur ou égal à ![]() à la recherche d’un éventuel diviseur de
à la recherche d’un éventuel diviseur de ![]() (noter que cette liste est vide si
(noter que cette liste est vide si ![]() 3, 5 ou 7).
3, 5 ou 7).
➣ Si un diviseur ![]() est détecté, on interrompt la recherche et
est détecté, on interrompt la recherche et ![]()
➣ Sinon, c’est que ![]() (et, bien sûr,
(et, bien sûr, ![]() est premier).
est premier).
Traitons à la main le cas n = 101, pour voir.
Pour commencer, la racine carrée entière de 101 est 10 puisque ![]() tandis que
tandis que ![]()
Ensuite, on recherche d’éventuels diviseurs de 101 parmi les entiers impairs de 3 à 9 :
- 101 n’est pas multiple de 3 car la somme de ses chiffres décimaux ne l’est pas,
- 101 n’est pas multiple de 5 car son chiffre des unités n’est ni 0 ni 5,
- 101 n’est pas multiple de 7 puisque
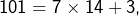
- Il est inutile de tester la divisibilité par 9 puisque 3 n’est déjà pas diviseur de 101.
→ Ceci prouve que 101 est un nombre premier.
Autre exemple, avec n = 323. La racine carrée entière de 323 est 17 (car ![]() tandis que
tandis que ![]() Aucun diviseur de 323 ne figure parmi les entiers 3, 5, 7, 11, 13.
Aucun diviseur de 323 ne figure parmi les entiers 3, 5, 7, 11, 13.
En revanche : ![]() Ainsi, 323 est un nombre composé, dont le PPFP est 17.
Ainsi, 323 est un nombre composé, dont le PPFP est 17.
Cet algorithme est connu depuis au moins 9 siècles ! Il apparaît dans le Liber Abaci, l’immense ouvrage achevé en 1202 par Leonardo Pisano (en français : Léonard de Pise, plus connu sous le pseudonyme de Fibonacci).


Pour des entiers un peu trop grands, cette méthode est toutefois impraticable et il serait illusoire d’espérer trouver le PPFP de cette manière. Imaginons en effet un nombre impair ![]() dont l’écriture décimale comporte une centaine chiffres :
dont l’écriture décimale comporte une centaine chiffres :
![]()
La racine carrée entière de ![]() est alors peu différente de
est alors peu différente de ![]() et notre algorithme va nous conduire à effectuer jusqu’à
et notre algorithme va nous conduire à effectuer jusqu’à ![]() tests de divisibilité (la moitié de
tests de divisibilité (la moitié de ![]() puisque les entiers pairs ne sont pas testés). Bien sûr, l’algorithme peut très bien se terminer plus tôt, mais si
puisque les entiers pairs ne sont pas testés). Bien sûr, l’algorithme peut très bien se terminer plus tôt, mais si ![]() est premier (ce que nous supposerons dans la suite), il devra se poursuivre jusque là !
est premier (ce que nous supposerons dans la suite), il devra se poursuivre jusque là !
En admettant que nous disposions d’un ordinateur capable d’effectuer en moyenne un million de tests par seconde, cela signifie que le temps de calcul sera de l’ordre de :
![]()
![]()
Cette durée est très supérieure à l’âge de l’Univers …
6 – L’infinité des nombres premiers
Il n’est pas évident a priori de savoir si la liste des nombres premiers se termine par un nombre premier plus grand que tous les autres ou si, au contraire, cette liste est interminable.
C’est à Euclide que revient le mérite d’avoir su prouver que pour tout nombre premier donné, il en existe un autre qui lui est supérieur; autrement dit, qu’il existe une infinité de nombres premiers. Ce résultat est apparu, il y a environ 23 siècles, dans les éléments d’Euclide, livre IX, proposition 20.
Voici l’argument.
Proposition 5
On suppose que ![]()
![]()
![]() sont des nombres premiers tous distincts et l’on note
sont des nombres premiers tous distincts et l’on note ![]() leur produit. On considère alors l’entier :
leur produit. On considère alors l’entier :
![]()
Si l’on avait ![]() pour un certain indice
pour un certain indice ![]() alors
alors ![]() diviserait évidemment
diviserait évidemment ![]() Mais comme
Mais comme ![]() divise
divise ![]()
![]() diviserait aussi
diviserait aussi ![]() autrement dit
autrement dit ![]() diviserait 1 : c’est absurde !
diviserait 1 : c’est absurde !
Le nombre premier ![]() ne figure donc pas dans la liste
ne figure donc pas dans la liste ![]()
Notons désormais ![]() le
le ![]() ème nombre premier :
ème nombre premier :
![]()
Pour tout ![]() posons :
posons :
![]()
Regardons pour les petites valeurs de ![]() (on note
(on note ![]() lorsque
lorsque ![]() est un nombre premier) :
est un nombre premier) :
Pour ![]() :
:
![]()
![]()
![]()
![]()
![]()
Mais pour
![]()
La réponse est donc négative. Quant à savoir si ![]() pour une infinité d’indices
pour une infinité d’indices ![]() (ou non), cette question demeure à ce jour sans réponse.
(ou non), cette question demeure à ce jour sans réponse.
On ne sait pas davantage s’il existe une infinité d’indices ![]() pour lesquels
pour lesquels ![]() est composé !
est composé !
Terminons en signalant la « conjecture de Fortune », du nom de l’anthropologue néo-zélandais Reo Franklin Fortune (1903 – 1979).
Notons ![]() le plus petit nombre premier plus grand que
le plus petit nombre premier plus grand que ![]() et intéressons-nous à l’écart
et intéressons-nous à l’écart ![]() Voici ce qu’on obtient pour les petites valeurs de
Voici ce qu’on obtient pour les petites valeurs de ![]() :
:
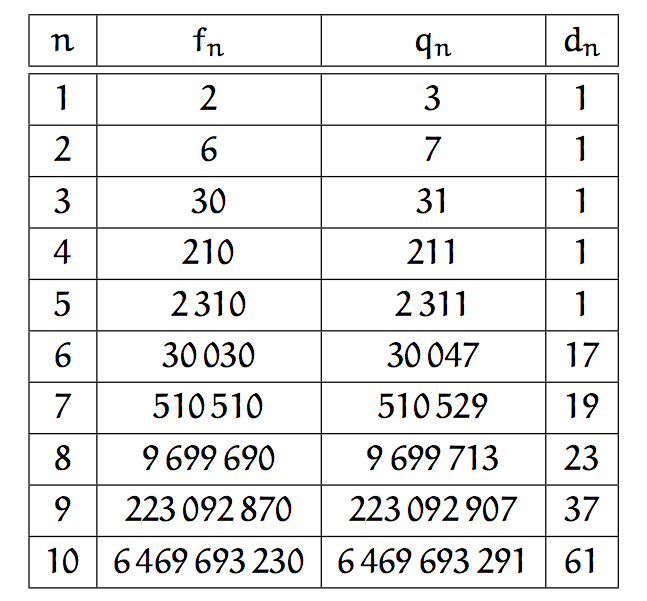
De façon assez surprenante, la valeur de ![]() semble être soit 1 soit un nombre premier.
semble être soit 1 soit un nombre premier.
Et ça continue … La conjecture a été testée jusqu’à ![]() environ, sans qu’aucun contre-exemple n’apparaisse… mais comme toujours, cela ne prouve rien ! La suite des nombres
environ, sans qu’aucun contre-exemple n’apparaisse… mais comme toujours, cela ne prouve rien ! La suite des nombres ![]() est référencée par l’OEIS (Online Encyclopedia of Integer Sequences) : voir ici
est référencée par l’OEIS (Online Encyclopedia of Integer Sequences) : voir ici
7 – Un théorème de Dirichlet
On peut adapter l’argument d’Euclide (présenté à la section précédente) pour démontrer qu’il existe une infinité de nombres premiers de la forme ![]()
Voici comment.
Etant donnés des nombres premiers ![]() distincts avec, pour chaque
distincts avec, pour chaque ![]() :
: ![]() considérons l’entier
considérons l’entier
![]()
![]()
![]()
Il est naturel de chercher à généraliser en se posant la question suivante :
Question
Etant donnés deux entiers ![]() premiers entre eux, existe-t-il une infinité de nombres premiers de la forme
premiers entre eux, existe-t-il une infinité de nombres premiers de la forme ![]() ?
?
La réponse est affirmative, comme l’a montré en 1837 le mathématicien allemand Peter Gustav Lejeune-Dirichlet (1805 – 1859). La preuve de ce résultat, parfois appelé « théorème de la progression arithmétique », est trop élaborée pour être présentée ici. Disons simplement que Dirichlet combine des notions de théorie des groupes (les caractères d’un groupe abélien fini) et d’analyse complexe pour établir la divergence de la série des inverses des nombres premiers congrus à ![]() modulo
modulo ![]()
8 – La rareté des nombres premiers
Combien existe-t-il de nombres premiers parmi les entiers inférieurs à ![]() ?
?
Un rapide décompte montre qu’il y en a ![]() à savoir :
à savoir : ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() et
et ![]()
Plus généralement, si ![]() on note
on note ![]() le nombre de nombres premiers qui sont inférieurs ou égaux à
le nombre de nombres premiers qui sont inférieurs ou égaux à ![]() :
:
![]()

Le symbole ![]() utilisé ici n’a évidemment rien à voir avec le rapport de la circonférence d’un cercle à son diamètre !
utilisé ici n’a évidemment rien à voir avec le rapport de la circonférence d’un cercle à son diamètre !
Je précise que cette notation est standard.
On sait (voir section 6) que l’ensemble des nombres premiers est infini, ce qui revient à dire que :
![]()
Afin de préciser cette affirmation un peu floue, disons plutôt que la proportion de nombres premiers parmi les entiers inférieurs à ![]() tend vers
tend vers ![]() lorsque
lorsque ![]() tend vers l’infini. Autrement dit :
tend vers l’infini. Autrement dit :
![]()
On exprime ceci en disant que la densité de l’ensemble des nombres premiers est nulle (ce résultat, non détaillé ici, pourrait faire l’objet d’un prochain article). Ceci revient à dire que la probabilité qu’un nombre pris au hasard dans ![]() soit premier tend vers
soit premier tend vers ![]() lorsque
lorsque ![]() tend vers l’infini.
tend vers l’infini.
Une nouvelle question, plus précise, se forme aussitôt : à quelle « vitesse » la raréfaction des nombres premiers se produit-elle ?
Autrement dit : quel est le comportement asymptotique de ![]() en l’infini ? Cette question fondamentale s’est posée il y a environ deux siècles et demi. On peut, schématiquement, décomposer le travail accompli par les mathématiciens en trois temps :
en l’infini ? Cette question fondamentale s’est posée il y a environ deux siècles et demi. On peut, schématiquement, décomposer le travail accompli par les mathématiciens en trois temps :
- Carl Friedrich Gauss (allemand, 1777 – 1855) et Adrien-Marie Legendre (français, 1752 – 1833) conjecturèrent vers la fin du XVIIIème siècle que :
![Rendered by QuickLaTeX.com \[\pi\left(x\right)\sim\frac{x}{\ln\left(x\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-97c5c6e13d506800f37e4d9c55d28ff1_l3.png)
- Pafnouti Lvovitch Tchebychev (russe, 1821 – 1894) s’approcha du résultat en montrant en
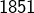 que, pour
que, pour  :
:
Tchebychev montra également que si![Rendered by QuickLaTeX.com \[0,9\:\frac{x}{\ln\left(x\right)}\leqslant\pi\left(x\right)\leqslant1,2\:\frac{x}{\ln\left(x\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-04e892091adc0d316baa9e4ab998bfa4_l3.png)
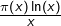 admet en
admet en 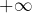 une limite, alors celle-ci est nécessairement égale à
une limite, alors celle-ci est nécessairement égale à 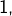 mais ne parvint pas à prouver l’existence de cette limite.
mais ne parvint pas à prouver l’existence de cette limite. - Enfin, à la toute fin du XIXème siècle Jacques Hadamard (français, 1865 – 1963) et Charles-Jean de la Vallée Poussin (belge, 1866 – 1962) démontrèrent indépendamment la conjecture formulée deux siècles plus tôt par Gauss et Legendre.
Ce résultat, publié en 1896, est le « théorème des nombres premiers ».
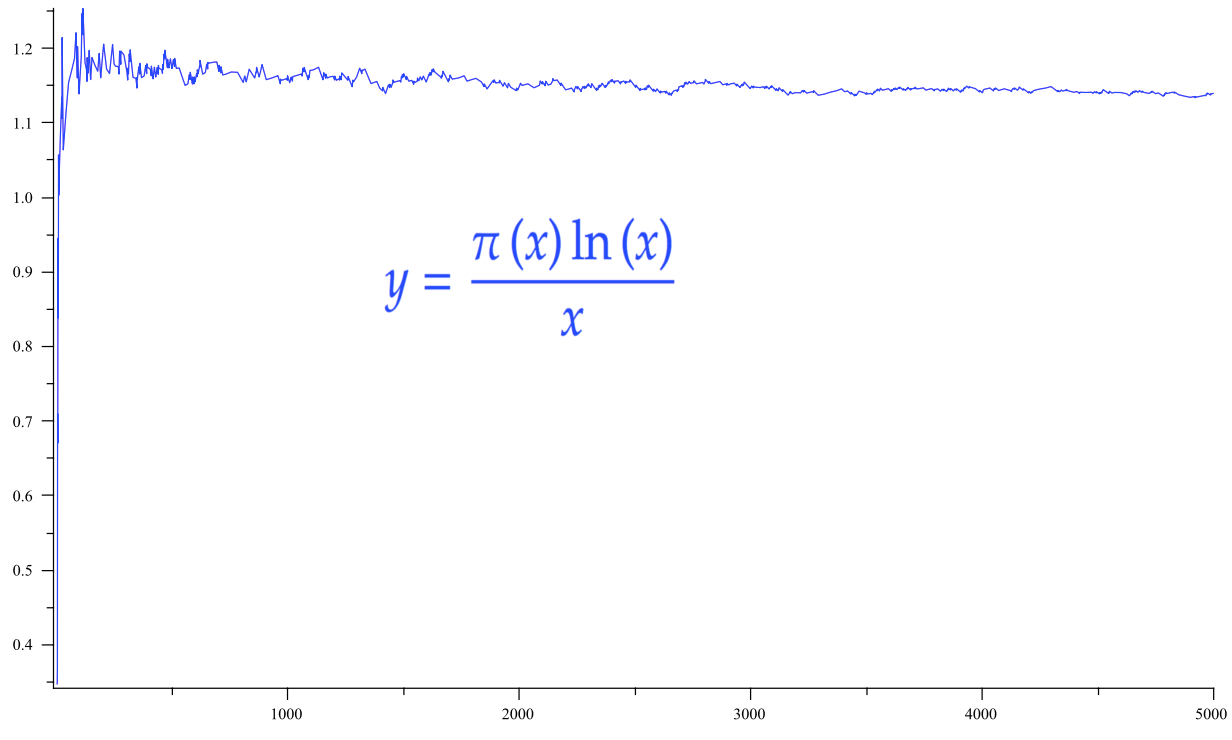
Le graphique ci-dessous montre une partie du graphe de la fonction ![]() : on visualise ainsi le fait que sa limite en
: on visualise ainsi le fait que sa limite en ![]() vaut
vaut ![]()
9 – Mersenne et Fermat
L’immense domaine que constitue l’étude des nombres premiers est jalonné de niches, où le promeneur non spécialiste (mais curieux) peut s’émerveiller de questions simples en apparence, qui cachent en leur sein des abimes de complexité et font intervenir des entiers de taille colossale.
A l’aube du XVIIème siècle, le moine Marin Mersenne (1588 – 1648) porta (comme d’autres avant lui) son regard sur les entiers de la forme ![]()
Il affirma – à juste titre – que si ![]() est premier, alors
est premier, alors ![]() est aussi premier. La réciproque de cette implication est fausse, et le plus petit contre-exemple apparaît avec
est aussi premier. La réciproque de cette implication est fausse, et le plus petit contre-exemple apparaît avec ![]() :
:
![]()
Ceci constitue une performance pour l’époque, même si cette liste comportait cinq erreurs.
En effet, les exposants 67 et 257 figuraient à tort dans cette liste, puisque :
![]()
![]()
![]()
En outre, trois autres exposants (61, 89 et 107) étaient manquants.
Malgré sa ténacité, Mersenne ne découvrit aucune structure, aucun motif régulier, qui lui aurait permis de savoir s’il existe – ou non – une infinité de nombres premiers de la forme ![]() Aujourd’hui encore, cette question est ouverte.
Aujourd’hui encore, cette question est ouverte.
On trouvera ici d’autres éléments d’informations sur les nombres de Mersenne.
C’est sensiblement à la même époque que Pierre de Fermat (160? – 1665), conseiller au parlement de Toulouse et génial mathématicien amateur, s’intéressa (entre autres choses !) aux nombres qui portent aujourd’hui son nom. Il montra que si ![]() et
et ![]() sont des entiers supérieurs ou égaux à 2 et si
sont des entiers supérieurs ou égaux à 2 et si ![]() est premier, alors
est premier, alors ![]() est pair et
est pair et ![]() est une puissance de
est une puissance de ![]() Ceci le conduisit à porter plus spécialement son attention sur les nombres, dits « de Fermat »,
Ceci le conduisit à porter plus spécialement son attention sur les nombres, dits « de Fermat », ![]()
En formulant l’hypothèse que tous les ![]() sont premiers, Fermat se trompa lourdement. On ne connaît aujourd’hui que cinq nombres premiers parmi les
sont premiers, Fermat se trompa lourdement. On ne connaît aujourd’hui que cinq nombres premiers parmi les ![]() (à savoir
(à savoir ![]()
![]()
![]()
![]() et
et ![]()
En dépit de leur talent, Mersenne et Fermat furent évidemment limités, dans leurs investigations, par la taille gigantesque de ces nombres. Ainsi, Fermat ne parvint pas à voir que ![]()
est composé (car multiple de ![]() comme l’a découvert Euler en 1732).
comme l’a découvert Euler en 1732).
Et pour un entier comme ![]() dont l’écriture décimale comporte
dont l’écriture décimale comporte ![]() chiffres ou bien
chiffres ou bien ![]() avec ses quelques
avec ses quelques ![]() chiffres, même le génial Euler ne pouvait pas faire grand chose.
chiffres, même le génial Euler ne pouvait pas faire grand chose.
L’avènement des ordinateurs a rendu possibles des calculs dépassant de très loin les rêves les plus fous des deux pionniers. Ce qui suit devrait donner une petite idée du chemin parcouru…
On sait aujourd’hui (janvier 2021) que ![]() est composé pour
est composé pour ![]() et le statut (premier ou composé) de
et le statut (premier ou composé) de ![]() est inconnu. On connaît en tout
est inconnu. On connaît en tout ![]() exposants
exposants ![]() pour lesquels
pour lesquels ![]() est composé. Pour autant, on ne connaît pas, en général, la DFP de ces nombres sauf pour sept d’entre eux : les
est composé. Pour autant, on ne connaît pas, en général, la DFP de ces nombres sauf pour sept d’entre eux : les ![]() pour
pour ![]()
Par exemple, on sait que :
![]()
Dernier résultat paru (Tom Greer, janvier 2021) :
![]()
Pour information, ![]() s’écrit avec plus de
s’écrit avec plus de ![]() chiffres décimaux !!!
chiffres décimaux !!!
La taille de ces entiers donne véritablement le vertige.
Ajoutons, pour finir, que nul ne sait s’il existe (ou non) une infinité de nombres de Fermat premiers.
Pour en savoir plus sur les nombres de Fermat et l’état d’avancement des recherches les concernant, on pourra consulter cette page.
10 – Nombres premiers et cryptographie
Le britannique Godfrey Harold Hardy (1877 – 1947) fut un mathématicien de premier plan, comme en témoignent la qualité et la profondeur de ses contributions à l’analyse et à la théorie des nombres. Sa renommée doit aussi beaucoup à l’étonnante et fructueuse collaboration qui est née de sa rencontre avec le génie mathématique indien Srinivasa Ramanujan.
Courant 1915, lors d’un exposé relatif aux nombres premiers, Hardy fit – avec une certaine dose de cynisme – le commentaire suivant :
Commentaire de G.H. Hardy
The theory of Numbers has always been regarded as one of the most obviously useless branches of Pure Mathematics. The accusation is one against which there is no valid defense; and it is never more just than when directed against the parts of the theory which are more particularly concerned with primes. A science is said to be useful if its development tends to accentuate the existing inequalities in the distribution of wealth, or more directly promotes the destruction of human life. The theory of prime numbers satisfies no such criteria. Those who pursue it will, if they are wise, make no attempt to justify their interest in a subject so trivial and so remote, and will console themselves with the thought that the greatest mathematicians of all ages have found it in it a mysterious attraction impossible to resist.
que l’on peut traduire comme suit :
La théorie des nombres a toujours été perçue comme l’une des branches les moins utiles des Mathématiques Pures. On ne pourra guère contester cette accusation, encore moins lorsqu’elle vise les parties de la théorie plus particulièrement liées aux nombres premiers. Une science est qualifiée d’utile si son développement contribue à accentuer les inégalités dans la répartition des richesses ou, lorsqu’il promeut plus directement la destruction de la vie humaine. La théorie des nombres premiers ne vérifie pas de tels critères. Ceux qui l’explorent ne tenteront pas, si toutefois ils sont doués de sagesse, de justifier l’intérêt qu’ils portent à un sujet si futile et isolé et se consoleront à l’idée que les plus grands mathématiciens de tous les temps y ont trouvé un attrait mystérieux, auquel il est impossible de se soustraire.
Il est assez frappant de constater qu’environ six décennies plus tard, les faits donnèrent tort – et de manière cinglante – à Hardy.
Avec l’apparition du commerce électronique et, plus généralement, dans tous les domaines où informatique et cryptographie se côtoient, les nombres premiers sont devenus tout simplement incontournables.
Largement utilisé à l’échelle planétaire, le système de cryptographie à clef publique RSA (du nom de ses trois inventeurs Rivest, Shamir et Adleman) donne un exemple significatif de cette interaction. Citons (en les traduisant) les auteurs :
Description RAS
Pour crypter un message, on commence par le représenter au moyen d’un entier M. On calcule ensuite ![]() où l’exposant
où l’exposant ![]() et l’entier
et l’entier ![]() sont connus publiquement,
sont connus publiquement, ![]() étant le produit de deux grands nombres premiers
étant le produit de deux grands nombres premiers ![]() et
et ![]() maintenus secrets. Le résultat de ce calcul constitue le cryptogramme
maintenus secrets. Le résultat de ce calcul constitue le cryptogramme ![]() Ce dernier peut ensuite être décrypté en calculant
Ce dernier peut ensuite être décrypté en calculant ![]() où l’exposant
où l’exposant ![]() est secret et vérifie
est secret et vérifie ![]() C’est la difficulté de factoriser
C’est la difficulté de factoriser ![]() (autrement dit de retrouver ses deux facteurs premiers
(autrement dit de retrouver ses deux facteurs premiers ![]() et
et ![]() ) qui garantit la sécurité de ce système.
) qui garantit la sécurité de ce système.
Le texte intégral de l’article
« A Method for Obtaining Digital Signatures and Public-Key Cryptosystems »
publié en 1978 dans la revue Communications of the ACM (Vol. 21-2) est disponible sur la page de Ronald L. Rivest.
Appendice – Quelques problèmes ouverts
Voici, pour finir, quelques célèbres questions non résolues (ou incomplètement résolues). Elles ont au moins un point en commun (outre le fait qu’elle portent toutes sur les nombres premiers) : leur énoncé est totalement élémentaire. La célèbre hypothèse de Riemann ne figure donc pas dans cette courte liste.
Les quatre premières questions constituent ce qu’on appelle les problèmes de Landau. Le mathématicien Edmund Landau les proposa, lors du cinquième congrès international des mathématiciens qui se tint à Cambridge en 1912.
Problème 1 – Existe-t-il une infinité de couples ![]() de nombres premiers vérifiant
de nombres premiers vérifiant ![]() ?
?
La conjecture des « nombres premiers jumeaux » consiste à répondre affirmativement à cette question. Le mathématicien chinois Jingrun Chen montra en 1966 l’existence d’une infinité de nombres premiers ![]() pour lesquels
pour lesquels ![]() est soit premier soit le produit de deux nombres premiers.
est soit premier soit le produit de deux nombres premiers.
En 2013, un autre mathématicien chinois, Yitang Zhang, prouva qu’il existe une infinité de couples ![]() de nombres premiers pour lesquels
de nombres premiers pour lesquels ![]() Cet écart a été réduit, depuis lors, à une valeur moindre, mais un écart de 2 semble, pour le moment, hors d’atteinte. Pour la petite histoire, Y. Zhang était titulaire d’un poste d’assistant avant de publier son travail. Il est désormais professeur à l’université de Santa Barbara, en Californie.
Cet écart a été réduit, depuis lors, à une valeur moindre, mais un écart de 2 semble, pour le moment, hors d’atteinte. Pour la petite histoire, Y. Zhang était titulaire d’un poste d’assistant avant de publier son travail. Il est désormais professeur à l’université de Santa Barbara, en Californie.

Problème 2 – Tout entier pair supérieur ou égal à ![]() est-il la somme de deux nombres premiers ?
est-il la somme de deux nombres premiers ?
En juin 1742, Goldbach proposa à Euler une conjecture selon laquelle tout entier ![]() est la somme de trois nombres premiers (Goldbach considérait que 1 est premier). A la fin du mois, Euler lui répondit qu’il était convaincu que tout entier pair supérieur ou égal à
est la somme de trois nombres premiers (Goldbach considérait que 1 est premier). A la fin du mois, Euler lui répondit qu’il était convaincu que tout entier pair supérieur ou égal à ![]() est la somme de deux nombres premiers, mais qu’il n’était pas capable de le prouver. Aujourd’hui encore, cet énoncé résiste. Cependant, une forme faible de la conjecture, à savoir que tout nombre impair supérieur ou égal à
est la somme de deux nombres premiers, mais qu’il n’était pas capable de le prouver. Aujourd’hui encore, cet énoncé résiste. Cependant, une forme faible de la conjecture, à savoir que tout nombre impair supérieur ou égal à ![]() est la somme de trois nombres premiers, a été prouvée en 2013 par le mathématicien péruvien Harald Helfgott.
est la somme de trois nombres premiers, a été prouvée en 2013 par le mathématicien péruvien Harald Helfgott.
On peut l’écouter dans cette vidéo réalisée en 2015 au CIRM.
Problème 3 – Etant donné un entier ![]() existe-t-il au moins un nombre premier compris entre
existe-t-il au moins un nombre premier compris entre ![]() et
et ![]() ?
?
La conjecture de Legendre affirme que c’est vrai quel que soit ![]() Le « postulat de Bertrand », selon lequel pour tout entier
Le « postulat de Bertrand », selon lequel pour tout entier ![]() il existe un nombre premier compris entre
il existe un nombre premier compris entre ![]() et
et ![]() fut démontré à la fin du XIXème siècle par Tchebytchev. On en trouve une très jolie preuve, due à P. Erdös, dans l’excellent livre Proofs from the Book
fut démontré à la fin du XIXème siècle par Tchebytchev. On en trouve une très jolie preuve, due à P. Erdös, dans l’excellent livre Proofs from the Book
Problème 4 – Existe-t-il une infinité de nombres premiers de la forme ![]() ?
?
Problème 5 – Existe-t-il une infinité de nombre de Mersenne premiers ?
Problème 6 – Existe-t-il une infinité de nombre de Fermat premiers ?
Problème 7 – Existe-t-il une infinité de nombre de Fibonacci premiers ?
Problème 8 – Existe-t-il une infinité de nombres premiers ![]() tels que
tels que ![]() soit aussi premier ?
soit aussi premier ?
Sophie Germain, mathématicienne française (1776 – 1831), démontra que si ![]() et
et ![]() sont premiers, alors l’équation diophantienne
sont premiers, alors l’équation diophantienne ![]() ne possède aucune solution dans
ne possède aucune solution dans ![]()
Problème 9 – Les nombres premiers de Wilson sont des nombres premiers ![]() tels que
tels que ![]() divise
divise ![]() On en connaît trois : 5, 13 et 563. En existe-t-il d’autres ?
On en connaît trois : 5, 13 et 563. En existe-t-il d’autres ?
Problème 10 – Si ![]() désigne le
désigne le ![]() ème nombre premier et si
ème nombre premier et si ![]() désigne le plus petit nombre premier supérieur au produit
désigne le plus petit nombre premier supérieur au produit ![]() est-il vrai que
est-il vrai que ![]() est, pour tout
est, pour tout ![]() égal à 1 ou bien à un nombre premier ?
égal à 1 ou bien à un nombre premier ?
Cette dixième et dernière question a été sommairement examinée à la section 6 du présent article.
Ainsi s’achève ce petit survol d’un domaine des mathématiques que je trouve absolument passionnant. Merci de vos commentaires, si vous partagez cette passion avec moi 🙂
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.








Excellent article. Les références sont claires et c’est très bien expliqué. Je ne sais pas si c’est normal, mais les bouquins ne s’affichent pas sur mon navigateur.
Merci pour votre sympathique commentaire. Concernant l’affichage des bouquins, non ce n’est pas normal. Je vais tâcher de régler cela rapidement.
Voilà, c’est réparé 🙂 Merci de me l’avoir signalé !
Selon une nouvelle définition mathématique, les nombres entiers naturels se divisent en deux ensembles dont l’un est la fusion de la suite des nombres premiers et des nombres zéro et un. Trois autres définitions, déduites de cette première, subdivisent l’ensemble des nombres entiers naturels en quatre classes de nombres aux propriétés arithmétiques propres et uniques. La distribution géométrique de ces différents types d’entiers naturels, dans de diverses matrices fermées, s’organise en ratios exacts de valeur 3/2 ou 1/1.
Bonjour et merci pour ce commentaire. Avez-vous des références à donner (articles, livres …) ?
S’agit-il d’observations empiriques (et si oui, lesquelles ?) ou bien connaissez-vous des théorèmes qui encadrent cette question de façon rigoureuse ?