
Etant donné un ensemble ![]() on note classiquement
on note classiquement ![]() l’ensemble des couples d’éléments de
l’ensemble des couples d’éléments de ![]()
Un couple ![]() est une structure ordonnée au sens où, si
est une structure ordonnée au sens où, si ![]() alors les couples
alors les couples ![]() et
et ![]() sont différents. Par contraste, la paire
sont différents. Par contraste, la paire ![]() , ensemble à deux éléments, est identique à la paire
, ensemble à deux éléments, est identique à la paire ![]() .
.
Une opération ![]() sur un ensemble
sur un ensemble ![]() n’est pas autre chose qu’une application de
n’est pas autre chose qu’une application de ![]() dans
dans ![]()
A chaque couple ![]() est associé un élément de
est associé un élément de ![]() qui dans ce contexte est noté
qui dans ce contexte est noté ![]()
L’opération ![]() est dite associative lorsque :
est dite associative lorsque :
![]()
On peut alors se passer des parenthèses et écrire simplement ![]()
Lorsqu’une opération ![]() n’est pas associative, l’expression
n’est pas associative, l’expression ![]() est ambigüe et ne doit pas être utilisée. Le rôle des parenthèses est, précisément, d’éliminer toute ambiguïté.
est ambigüe et ne doit pas être utilisée. Le rôle des parenthèses est, précisément, d’éliminer toute ambiguïté.
Dans la formule ci-dessus, les parenthèses sont déplacées mais l’ordre des éléments n’est pas modifié ! La question de l’associativité ne doit donc pas être confondue avec celle de la commutativité. L’opération ![]() est dite commutative lorsque
est dite commutative lorsque ![]() quel que soit le couple
quel que soit le couple ![]()
Cet article rassemble quelques remarques au sujet des opérations associatives.
1 – Exemples et contre-exemples immédiats
■ L’addition et la multiplication dans ![]() sont des opérations associatives.
sont des opérations associatives.
■ Même chose pour la composition des applications. Si ![]() est un ensemble et si
est un ensemble et si ![]() désigne l’ensemble des applications de
désigne l’ensemble des applications de ![]() dans lui-même, alors étant données
dans lui-même, alors étant données ![]()
![]() et
et ![]() dans
dans ![]() :
:
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left[\left(f\circ g\right)\circ h\right]\left(a\right) & = \left(f\circ g\right)\left(h\left(a\right)\right)\\& = f\left(g\left(h\left(a\right)\right)\right)\\& = f\left(\left(g\circ h\right)\left(a\right)\right)\\& = \left[f\circ\left(g\circ h\right)\right]\left(a\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-73feb8878f004d063da5977ad94bdcce_l3.png)
■ Notons ![]() l’ensemble des suites finies à termes dans un ensemble non vide
l’ensemble des suites finies à termes dans un ensemble non vide ![]() On dit que
On dit que ![]() est l’alphabet et que
est l’alphabet et que ![]() est l’ensemble des mots sur
est l’ensemble des mots sur ![]() Dans ce contexte, une suite finie est notée simplement en juxtaposant ses termes (dans l’ordre des indices croissants).
Dans ce contexte, une suite finie est notée simplement en juxtaposant ses termes (dans l’ordre des indices croissants).
Deux mots ![]() et
et ![]() peuvent être concaténés (càd : mis « bout à bout ») pour former le mot
peuvent être concaténés (càd : mis « bout à bout ») pour former le mot ![]()
Par exemple si ![]()
![]() et
et ![]() alors
alors ![]() L’opération de concaténation ainsi définie est clairement associative.
L’opération de concaténation ainsi définie est clairement associative.
■ En revanche, la soustraction dans ![]() n’est pas associative :
n’est pas associative :
![]()
■ L’exponentiation (opération « puissance ») dans ![]() n’est pas non plus associative puisque :
n’est pas non plus associative puisque :
![]()
Il y a une raison simple à cela. On peut, a priori, hésiter entre deux interprétations de l’expression ![]() …
…
- soit en parenthésant à gauche :
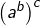
- soit en parenthésant à droite :
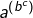
Mais on sait bien que ![]() . Il est donc naturel de convenir que l’expression
. Il est donc naturel de convenir que l’expression ![]() désigne
désigne ![]()
■ Dans un espace vectoriel euclidien orienté de dimension 3, le produit vectoriel n’est pas associatif. On sait par exemple que si ![]() est une base orthonormale directe, alors
est une base orthonormale directe, alors ![]() tandis que
tandis que ![]()
Voici maintenant un exemple un peu plus consistant.
2 – Différence symétrique
Etant donné un ensemble ![]() l’ensemble des parties de
l’ensemble des parties de ![]() est noté
est noté ![]() et le complémentaire dans
et le complémentaire dans ![]() d’une partie
d’une partie ![]() est noté
est noté ![]()
On définit dans ![]() une opération notée
une opération notée ![]() , en posant pour tout couple
, en posant pour tout couple ![]() de parties de
de parties de ![]() :
:
![]()
Les opérations d’union (symbole ![]() ) et d’intersection (symbole
) et d’intersection (symbole ![]() ) correspondent respectivement aux connecteurs logiques OU (inclusif) et ET. Dans cette analogie, l’opération
) correspondent respectivement aux connecteurs logiques OU (inclusif) et ET. Dans cette analogie, l’opération ![]() correspond au fameux XOR, alias « ou exclusif » (en anglais : eXclusive OR).
correspond au fameux XOR, alias « ou exclusif » (en anglais : eXclusive OR).
Illustration dynamique
On voit ici un ensemble ![]() et deux sous-ensembles
et deux sous-ensembles ![]() de
de ![]() .
.
En cliquant sur l’un quelconque des 8 boutons de gauche, on fait apparaître la partie correspondante (ou son complémentaire dans ![]() si le bouton
si le bouton ![]() est activé).
est activé).
Proposition
L’opération ![]() est associative.
est associative.
Preuve (cliquer pour déplier / replier)
Soient ![]() trois parties de
trois parties de ![]() Par définition de
Par définition de ![]() :
:
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left(A\thinspace\triangle\thinspace B\right)\thinspace\triangle\thinspace C & = \left[\left(A\cap\overline{B}\right)\cup\left(\overline{A}\cap B\right)\right]\thinspace\triangle\thinspace C\\& = \left(\left(\left(A\cap\overline{B}\right)\cup\left(\overline{A}\cap B\right)\right)\cap\overline{C}\right)\cup\left(\overline{\left(A\cap\overline{B}\right)\cup\left(\overline{A}\cap B\right)}\cap C\right)\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-587810736617f9a1d7fec61a77f21c4b_l3.png)
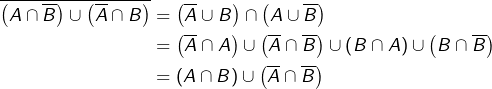
![]()
On pourrait ensuite développer ![]() et constater qu’on parvient au même résultat.
et constater qu’on parvient au même résultat.
Mais on peut être plus malin 🤓
L’expression encadrée ci-dessus est invariante par permutation circulaire : elle reste inchangée si le triplet ![]() est remplacé par
est remplacé par ![]()
En effet, cette permutation transforme le 1er terme de cette union en le 2ème, le 2ème en le 3ème, le 3ème en le 1er; quant au 4ème, il est invariant :
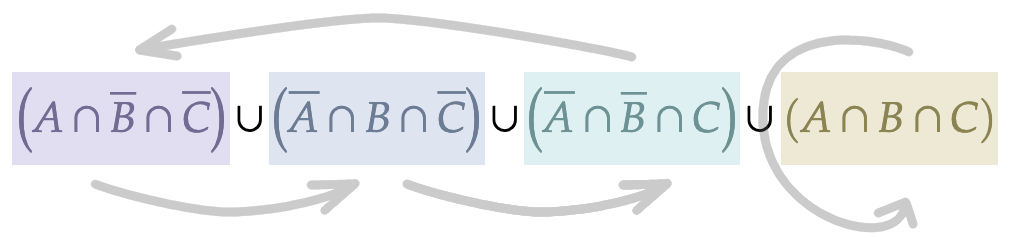
Autrement dit :
![]()
![]()
Dans la section 5, nous reviendrons sur cette question en adoptant un angle de vue différent.
3 – Invariance circulaire & Associativité
Soit ![]() un ensemble muni d’une opération
un ensemble muni d’une opération ![]()
Définition
L’opération ![]() est dite circulairement invariante lorsque :
est dite circulairement invariante lorsque :
![]()
On peut alors énoncer :
Proposition
Si ![]() est commutative et circulairement invariante, alors
est commutative et circulairement invariante, alors ![]() est associative.
est associative.
La justification de cette affirmation est immédiate ! Mais en dépit de sa simplicité, cette proposition a montré son utilité : elle a permis, à la section précédente, d’alléger la preuve de l’associativité de la différence symétrique. En voici une variante :
Proposition Bis
Si ![]() est circulairement invariante et admet un élément neutre,
est circulairement invariante et admet un élément neutre,
alors ![]() est commutative et associative.
est commutative et associative.
Notons ![]() l’élément neutre. Pour tout
l’élément neutre. Pour tout ![]() :
: ![]() c’est-à-dire
c’est-à-dire ![]()
L’opération est ainsi commutative et donc associative grâce au point précédent.
Notons que, dans la proposition-bis, l’hypothèse d’invariance circulaire n’est pas suffisante à elle seule.
Voici un exemple d’une opération circulairement invariante, mais qui n’est ni commutative ni associative (le secret est l’absence d’élément neutre) :
Exemple
Munissons ![]() de l’opération définie par :
de l’opération définie par :
![]()
![]()
![]()
Mais ![]() n’est pas commutative puisque :
n’est pas commutative puisque :
![]()
![]()
![]()
4 – Associativité et Inversibilité
Lorsqu’une opération ![]() sur un ensemble
sur un ensemble ![]() possède un élément neutre
possède un élément neutre ![]() la notion d’inversibilité apparaît aussitôt.
la notion d’inversibilité apparaît aussitôt.
Définition
Un élément ![]() est dit inversible s’il existe
est dit inversible s’il existe ![]() tel que :
tel que :
![]()
On notera l’emploi de l’article indéfini : un inverse car il n’y a aucune garantie d’unicité a priori.
Voici un exemple montrant que certains éléments peuvent posséder plusieurs inverses, tandis que d’autres n’en possèdent qu’un seul, ou même aucun.
Exemple
Munissons ![]() de l’opération
de l’opération ![]() définie par :
définie par :
![]()
On trouve les (éventuels) inverses d’un réel ![]() en résolvant l’équation
en résolvant l’équation ![]() qui est une simple équation du second degré.
qui est une simple équation du second degré.
Il est facile de voir que :
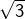 possède deux inverses, à savoir
possède deux inverses, à savoir 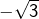 et
et 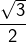 ,
,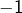 possède un seul inverse : lui-même,
possède un seul inverse : lui-même,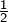 ne possède pas d’inverse.
ne possède pas d’inverse.
Cette « bizarrerie » est rendue possible par le fait que, dans cet exemple, l’opération n’est pas associative, ce qu’on peut constater directement :
![]()
![]()
Proposition
Soit ![]() une opération associative sur
une opération associative sur ![]() admettant un élément neutre
admettant un élément neutre ![]()
Si ![]() est inversible, alors il existe un unique inverse pour cet élément.
est inversible, alors il existe un unique inverse pour cet élément.
Cet inverse, s’il existe, est généralement noté ![]()
Soit ![]() et soient
et soient ![]() deux inverses de
deux inverses de ![]() Alors :
Alors :
![]()
Remarque
Ce simple calcul prouve un résultat un peu meilleur. Si un élément possède inverse à gauche et un inverse à droite, alors ces deux-là sont égaux et donc ![]() est inversible tout court.
est inversible tout court.
5 – Retour sur l’associativité de la différence symétrique
![]() désigne à nouveau un ensemble quelconque.
désigne à nouveau un ensemble quelconque.
Définissons une opération notée ![]() dans l’ensemble des applications de
dans l’ensemble des applications de ![]() dans
dans ![]()
Pour tout couple ![]() d’applications de
d’applications de ![]() dans
dans ![]() posons :
posons :
![]()
Il est facile de voir que ![]() est associative : ceci découle immédiatement du fait que
est associative : ceci découle immédiatement du fait que ![]() est elle-même associative dans
est elle-même associative dans ![]()
Notons ensuite ![]() la fonction indicatrice d’une partie
la fonction indicatrice d’une partie ![]() de
de ![]() . C’est l’application
. C’est l’application ![]() qui à tout
qui à tout ![]() associe 1 si
associe 1 si ![]() et 0 sinon.
et 0 sinon.
On constate que, pour tout couple ![]() de parties de
de parties de ![]() :
:
![]()
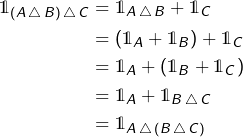
![]()
![]()
Nous avons établi d’une seconde manière l’associativité de ![]()
Remarque
En fait, on peut définir une seconde opération dans ![]() en posant :
en posant :
![]()
Point de terminologie : un tel anneau, dont chaque élément est idempotent (égal son carré) est appelé un anneau de Boole.
6 – Nombre de parenthésages d’un produit
Soit ![]() une opération sur un ensemble
une opération sur un ensemble ![]() non supposée associative.
non supposée associative.
Etant donnés un entier ![]() et des éléments
et des éléments ![]() de
de ![]() l’expression :
l’expression :
![]()
Afin de lever cette ambiguïté, il faut choisir un parenthésage. Et de nombreuses possibilités se présentent …
➡ Si ![]() il existe 2 parenthésages possibles :
il existe 2 parenthésages possibles :
![]()
➡ Si ![]() il en existe 5 :
il en existe 5 :
![Rendered by QuickLaTeX.com \[\begin{array}{c}\left(\left(x_{1}\star x_{2}\right)\star x_{3}\right)\star x_{4}\\\left(x_{1}\star\left(x_{2}\star x_{3}\right)\right)\star x_{4}\\\left(x_{1}\star x_{2}\right)\star\left(x_{3}\star x_{4}\right)\\x_{1}\star\left(\left(x_{2}\star x_{3}\right)\star x_{4}\right)\\x_{1}\star\left(x_{2}\star\left(x_{3}\star x_{4}\right)\right)\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f41c1a4354b42df7b98e567e75bcf971_l3.png)
Il est naturel de se demander quel est, plus généralement, le nombre ![]() de parenthésages — formellement différents — que l’on peut envisager pour un produit de
de parenthésages — formellement différents — que l’on peut envisager pour un produit de ![]() facteurs.
facteurs.
On peut répondre à cette question en raisonnant par récurrence.
Trivialement : ![]()
Etant donnés ![]() et des éléments
et des éléments ![]() le calcul de
le calcul de ![]() ne peut être envisagé qu’après avoir mis en évidence deux facteurs, disons
ne peut être envisagé qu’après avoir mis en évidence deux facteurs, disons ![]() et
et ![]() (pour un certain entier
(pour un certain entier ![]() , lesquels doivent à leur tour être parenthésés. Le premier facteur peut être parenthésé de
, lesquels doivent à leur tour être parenthésés. Le premier facteur peut être parenthésé de ![]() façons et le second peut l’être de
façons et le second peut l’être de ![]() façons.
façons.
On voit ainsi (après vérification directe pour ![]() ) que :
) que :
![Rendered by QuickLaTeX.com \[\boxed{\forall n\geqslant2,\thinspace P_{n}=\sum_{k=1}^{n-1}P_{k}P_{n-k}}\qquad\left(\heartsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c2114d9708eb78f298026fb37ef0249d_l3.png)
Il est facile de programmer (ci-dessous en Python) le calcul des premiers termes de la suite ![]() . Ces entiers sont stockés dans une liste, au fur et à mesure de l’avancement du calcul :
. Ces entiers sont stockés dans une liste, au fur et à mesure de l’avancement du calcul :
def calculP(nmax):
if (nmax < 2):
print ('Entrer un entier n > 1')
else:
p = [1,1]
for n in range (3, nmax + 1):
s = 0
for k in range (1,n):
s += p[k-1] * p[n-k-1]
p.append(s)
return pLa fonction calculP accepte un entier ![]() et renvoie la liste
et renvoie la liste ![]()
Les entiers ![]() pour
pour ![]() ont été calculés de cette façon :
ont été calculés de cette façon :
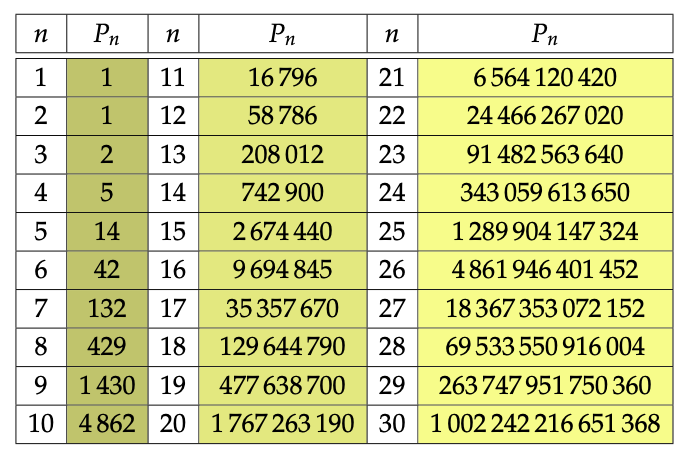
Le moins qu’on puisse dire, c’est que cette suite grimpe rapidement !
Afin de quantifier cette impression de croissance rapide, il nous faut trouver une estimation asymptotique de ![]() lorsque
lorsque ![]() . C’est l’objet de la section 7.
. C’est l’objet de la section 7.
Avant cela, voici comment on peut énumérer les ![]() parenthésages pour un
parenthésages pour un ![]() donné :
donné :
def car(n):
return chr(64+n)
def aux(n, start):
if (n == 1):
return [car(start)]
elif (n == 2):
return [car(start) + car(start+1)]
else:
res = []
for k in range(1,n):
g = aux (k, start)
d = aux (n-k, start+k)
for i in range(len(g)):
for j in range(len(d)):
gi = g[i]
dj = d[j]
if (len(gi) == 1):
if (len(dj) > 1):
res.append(g[i]+'('+d[j]+')')
else:
res.append(g[i]+d[j])
else:
if (len(dj) > 1):
res.append('('+g[i]+')('+d[j]+')')
else:
res.append('('+g[i]+')'+d[j])
return res
def enumP (n):
if (n > 10):
print ('trop grand, désolé ...')
else:
sol = aux (n, 1)
for i in range(len(sol)):
print (sol[i])La fonction enumP, appliqué à un entier (au maximum 10 pour ne pas que ça devienne délirant), affiche ligne par ligne les ![]() parenthésages. Par exemple :
parenthésages. Par exemple :
>>> enumP(5)
A(B(C(DE)))
A(B((CD)E))
A((BC)(DE))
A((B(CD))E)
A(((BC)D)E)
(AB)(C(DE))
(AB)((CD)E)
(A(BC))(DE)
((AB)C)(DE)
(A(B(CD)))E
(A((BC)D))E
((AB)(CD))E
((A(BC))D)E
(((AB)C)D)E7 – La suite  démasquée
démasquée
Nous allons utiliser la puissante technique de la fonction génératrice.
L’idée est d’introduire la série entière ![]() et de trouver une relation (typiquement une équation fonctionnelle ou différentielle) vérifiée par sa somme. Notons
et de trouver une relation (typiquement une équation fonctionnelle ou différentielle) vérifiée par sa somme. Notons ![]() son rayon de convergence.
son rayon de convergence.

Il n’est pas évident que ![]()
On pourrait l’établir au préalable au moyen d’une majoration adéquate de ![]() mais nous allons prendre l’ennemi à revers 😉
mais nous allons prendre l’ennemi à revers 😉
Supposons temporairement qu’on ait ![]() et posons, pour tout
et posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[f\left(t\right)=\sum_{n=1}^{\infty}P_{n}t^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6931cf0174d386f549473dd1e346c424_l3.png)
![Rendered by QuickLaTeX.com \[\forall n\geqslant2,\thinspace P_{n}=\sum_{k=0}^{n}P_{k}P_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7bd452906dc9c2f12923b87b5e7f0e3a_l3.png)
Attention : cette relation n’est pas valable pour ![]() En effet :
En effet : ![]() alors que
alors que ![]()
Pour tout ![]() :
:
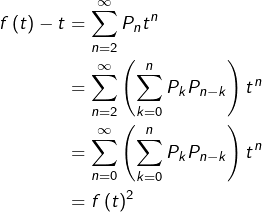
Ainsi ![]() et donc
et donc ![]() Mais comme
Mais comme ![]() alors
alors ![]()
En résolvant l’équation ![]() on voit que :
on voit que :
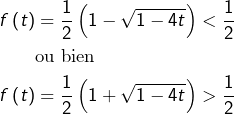
Comme ![]() est continue sur
est continue sur ![]() et vu que
et vu que ![]() le théorème des valeurs intermédiaires montre que
le théorème des valeurs intermédiaires montre que ![]() ne prend pas de valeurs supérieures à
ne prend pas de valeurs supérieures à ![]() Il est donc nécessaire que :
Il est donc nécessaire que :
![]()
Maintenant, il est classique que pour ![]() fixé :
fixé :
![Rendered by QuickLaTeX.com \[\forall t\in\left]-1,1\right[,\thinspace\left(1+t\right)^{\alpha}=\sum_{n=0}^{\infty}\binom{\alpha}{n}t^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-98a6819501b510e8327d5af8ac49942a_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{1-4t}=\sum_{n=0}^{\infty}\binom{{\scriptstyle {1/2}}}{n}\left(-4t\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2b142f37658a2edf04023863096d746_l3.png)
![Rendered by QuickLaTeX.com \[f\left(t\right)=\sum_{n=1}^{\infty}\frac{1}{n}\binom{2n-2}{n-1}t^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a37f27a076df07c9517d6e81defdb048_l3.png)
Ce raisonnement par condition nécessaire (voir cet article pour la signification de cette expression) nous a mis sur les rails. Nous savons maintenant ce qu’il nous faut prouver :
Proposition
Pour tout ![]() :
:
![]()
Posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[g\left(t\right)=\frac{1}{2}\left(1-\sqrt{1-4t}\right)=\sum_{n=0}^{\infty}a_{n}t^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-debb61f131137e2435ad222fdb0d033b_l3.png)
![Rendered by QuickLaTeX.com \[\forall n\geqslant2,\thinspace a_{n}=\sum_{k=0}^{n}a_{k}a_{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07218044524f856a2a5eb8d77a630c85_l3.png)
Comme ![]() il en résulte que les suites
il en résulte que les suites ![]() et
et ![]() sont confondues (elles vérifient la même « condition initiale » et la même formule de récurrence) et la formule
sont confondues (elles vérifient la même « condition initiale » et la même formule de récurrence) et la formule ![]() est démontrée.
est démontrée.
Pour finir, la formule de Stirling (voir cet article pour une preuve) dit que, lorsque ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[ \boxed{P{n}\sim\frac{4^{n-1}}{n^{3/2}\sqrt{\pi}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9f80f68a17118cdd5aa18b12955cb1be_l3.png)
Si l’on note ![]() cet équivalent alors
cet équivalent alors ![]() à comparer à
à comparer à ![]()
Il serait injuste de terminer cette section sans signaler que les entiers ![]() constituent un classique des questions de combinatoire, puisqu’il s’agit (à un décalage d’indice près) des nombres de Catalan (une célèbre conjecture de Catalan a été évoquée dans cet article).
constituent un classique des questions de combinatoire, puisqu’il s’agit (à un décalage d’indice près) des nombres de Catalan (une célèbre conjecture de Catalan a été évoquée dans cet article).

8 – Combien d’opérations associatives ?
Une question classique de combinatoire consiste à dénombrer les opérations sur un ensemble fini, qui satisfont une condition spécifique donnée. On considère donc un ensemble ![]() de cardinal
de cardinal ![]()
Pour commencer, vu qu’une opération sur ![]() est une application de
est une application de ![]() dans
dans ![]() il existe en tout :
il existe en tout :
![]()

Comme cela a été signalé à la section 1 :
il faut comprendre que ![]() désigne
désigne ![]()
Cet entier prend rapidement des valeurs énormes.
Par exemple, sur un ensemble à 4 éléments, on peut définir ![]() c’est-à-dire 4 294 967 296 opérations !!
c’est-à-dire 4 294 967 296 opérations !!
Et sur un ensemble à 10 éléments, le nombre d’opérations passe à ![]() (un 1 suivi de cent zéros) … ce qui est tout bonnement impossible à se représenter concrètement (voir quand même cet article pour une interprétation amusante d’un autre entier colossal : la factorielle de 52).
(un 1 suivi de cent zéros) … ce qui est tout bonnement impossible à se représenter concrètement (voir quand même cet article pour une interprétation amusante d’un autre entier colossal : la factorielle de 52).
Intéressons-nous maintenant à une propriété ![]() que peut éventuellement posséder une opération sur
que peut éventuellement posséder une opération sur ![]() Le nombre d’opérations sur
Le nombre d’opérations sur ![]() possédant cette propriété sera noté
possédant cette propriété sera noté ![]()
Le calcul de ![]() est plus ou moins aisé, selon la nature de
est plus ou moins aisé, selon la nature de ![]()
Je vous propose d’obtenir une formule explicite pour ![]() dans chacun des cas suivants :
dans chacun des cas suivants :
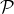 = commutativité
= commutativité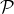 = posséder un élément neutre
= posséder un élément neutre
Si vous trouvez la réponse à l’une au moins de ces deux questions, n’hésitez pas à m’en faire part et votre contribution pourra être mise en ligne, en annexe à cet article.
Le titre de cette section soulève, quant à lui, une question nettement moins commode … en effet, aucune formule explicite n’a été trouvée à ce jour pour le nombre d’opérations associatives sur un ensemble fini. Parmi les travaux de recherche récents consacrés à cette question, on peut citer la thèse de Andreas Distler, soutenue en 2010 à l’université de Saint-Andrews.
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Bonjour Monsieur,
Je vous remercie pour votre réponse très détaillée !
C’est bien compris pour l’unicité du neutre, lorsqu’il y a existence et pour une opération donnée.
Je comprends aussi (désormais !) le raisonnement qui passe en revue tous les éléments comme neutre potentiel.
Je vous souhaite une bonne journée,
A bientôt
Bonjour Monsieur,
Merci pour cet article instructif et détaillé.
Pour les questions de fin : je tente ma chance 😊
Considérons un tableau carré de n lignes et n colonnes. Afin que cela soit plus clair, on peut ajouter une colonne (qui n’appartient pas au tableau !) à gauche de la première colonne avec dans celle-ci tous les éléments de l’ensemble E à n éléments -donc distincts- (notons les : X1, …, Xn, notons de plus * une loi de composition interne sur E). Procédons de façon analogue en ajoutant une ligne au-dessus de la première ligne avec les éléments de E. Il est alors facile de poser et visualiser que l’élément de la ligne i et de la colonne j du tableau est Xi*Xj.
0) Pour une loi donnée, chaque « case » du tableau peut donner lieu à n possibilités, on retrouve donc le fait qu’il y n^(n^2) lois possibles sur E, puisque le tableau comporte n^2 cases ;
1) Nous cherchons désormais à dénombrer les lois commutatives sur E. Raisonnons de nouveau à l’aide du tableau, celui-ci est composé d’une diagonale, d’un triangle inférieur et d’un triangle supérieur. La commutativité signifie que la connaissance d’un des deux triangles détermine l’autre triangle. De ce fait l’exposant sera cette fois-ci le cardinal de la diagonale auquel on ajoute celui d’un triangle (ce qui donne le cardinal d’un triangle un peu plus grand). Le nombre de lois commutatives sur E est donc n^(n(n+1)/2) ;
2) Nous cherchons le nombre de lois sur E possédant un unique élément neutre. Fixons Xn comme étant l’élément neutre. Ainsi la dernière ligne (et la dernière colonne) est la liste des éléments de E, quelle que soit la loi possédant un élément neutre. Nous sommes ramenés à un tableau carré de taille n-1, mais avec toujours n possibilités pour chaque case, le nombre cherché est donc n^((n-1)^2).
->on suppose implicitement que toutes ces lois possédant un élément neutre ont le même élément neutre (ce qui est peut-être faux). J’ai l’impression que ce n’est pas un problème dans le cadre de ce dénombrement ?
2)bis S’il existe k éléments neutres distincts (est-ce possible?), nous sommes ramenés à un tableau carré de taille n-k, le nombre cherché est donc dans ce cas n^((n-k)^2)
3) Ce n’était pas demandé, mais puisque ça ne coûte pas cher 😊, nous voyons aisément en combinant les raisonnements précédents, que le nombre de lois commutatives sur E possédant un unique élément neutre est n^(n(n-1)/2).
Bien à vous.
Bonjour et désolé pour le délai de réponse.
Ce qui vous expliquez dans votre préambule est correct. Pour le formuler un peu différemment : une opération sur un ensemble de cardinal
de cardinal  n’étant rien d’autre qu’une application de
n’étant rien d’autre qu’une application de 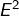 dans
dans  , il existe au total
, il existe au total 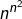 opérations, d’après la formule générale donnant le nombre d’applications d’un ensemble fini
opérations, d’après la formule générale donnant le nombre d’applications d’un ensemble fini 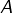 vers un ensemble fini
vers un ensemble fini 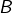 , à savoir
, à savoir 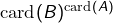 .
.
Ok aussi pour votre 1er point, que je reformule à ma façon (mais sans rien ajouter à votre preuve … simple variante de rédaction). Enumérons les éléments de en posant
en posant 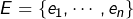 et notons
et notons 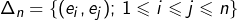 (ce qui correspond très exactement à votre triangle supérieur, diagonale comprise). Se donner une opération commutative sur
(ce qui correspond très exactement à votre triangle supérieur, diagonale comprise). Se donner une opération commutative sur  revient à se donner une application de
revient à se donner une application de 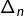 vers
vers  . Il existe donc
. Il existe donc 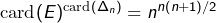 telles opérations.
telles opérations. et
et 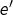 sont neutres, alors
sont neutres, alors 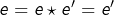 , la première égalité découlant du fait que
, la première égalité découlant du fait que 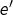 est neutre et la seconde du fait que
est neutre et la seconde du fait que  est neutre. Bref, soit il n’existe pas de neutre, soit il en existe un seul. A partir de là, on va dénombrer dans un premier temps les opérations pour lesquelles un élément
est neutre. Bref, soit il n’existe pas de neutre, soit il en existe un seul. A partir de là, on va dénombrer dans un premier temps les opérations pour lesquelles un élément  particulier est neutre. Notons
particulier est neutre. Notons 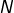 leur nombre, qui ne dépend pas de la valeur de
leur nombre, qui ne dépend pas de la valeur de  . Le nombre d’opérations possédant un neutre sera alors donné par
. Le nombre d’opérations possédant un neutre sera alors donné par 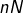 . Enfin, se donner une opération pour laquelle
. Enfin, se donner une opération pour laquelle  est neutre revient à se donner une application de
est neutre revient à se donner une application de 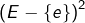 dans
dans  , donc
, donc 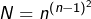 . Finalement, il existe
. Finalement, il existe 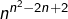 opérations possédant un neutre.
opérations possédant un neutre.
Concernant le dénombrement des opérations possédant un neutre, une petite erreur s’est glissée dans votre raisonnement. Il ne peut en effet pas exister plus d’un élément neutre, car si
On termine avec les opérations commutatives possédant un neutre. Un raisonnement similaire montre qu’il en existe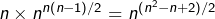 .
.