Lettre I
IDENTITÉ (application)
Etant donné un ensemble non vide ![]() on appelle identité de
on appelle identité de ![]() (ou application identique de
(ou application identique de ![]() l’application
l’application
![]()
Le graphe de ![]() est la diagonale de
est la diagonale de ![]() c’est-à-dire l’ensemble
c’est-à-dire l’ensemble ![]()
D’évidence, ![]() est une bijection qui coïncide avec sa bijection réciproque. Plus généralement, toute application
est une bijection qui coïncide avec sa bijection réciproque. Plus généralement, toute application ![]() telle que
telle que ![]() est bijective et coïncide avec sa réciproque (une telle application est appelée une involution).
est bijective et coïncide avec sa réciproque (une telle application est appelée une involution).
Si ![]() sont deux ensembles non vides, alors pour toute application
sont deux ensembles non vides, alors pour toute application ![]() :
:
![]()
![]()
En algèbre linéaire : si ![]() est un espace vectoriel sur un corps
est un espace vectoriel sur un corps ![]() les endomorphismes de la forme
les endomorphismes de la forme ![]() (pour
(pour ![]() sont appelés homothéties. Ils constituent le centre de la
sont appelés homothéties. Ils constituent le centre de la ![]() algèbre
algèbre ![]()
IDENTITÉ REMARQUABLE
On entend généralement par identité remarquable une égalité faisant intervenir une ou plusieurs variable(s), qui est vraie pour toute(s) valeur(s) de la (des) variable(s).
Les exemples les plus célèbres sont certainement :
(1) ![]()
(2) ![]()
Cette vidéo aborde de manière élémentaire la question des identités remarquables.
La relation (1) se généralise en la formule du binôme :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\forall\left(a,b\right)\in\mathbb{C}^{2},\thinspace\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k}b^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f8b1ea977a5ed4d7480d6eb1a7f394d_l3.png)
La relation (2) se généralise sous la forme :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}-\left\{ 0,1\right\} ,\forall\left(a,b\right)\in\mathbb{C}^{2},\thinspace a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{n-k}b^{k-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c73bd46f1a641ab8979e76ae6d743ec6_l3.png)
Voici quelques identités remarquables, plus « exotiques » :
Exemple 1
Pour tout ![]() :
:
![]()
Exemple 2
Pour tout ![]() :
:
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left(a+bj+cj^{2}\right)\left(a+bj^{2}+cj\right) & = & a^{2}+b^{2}+c^{2}-ab-ac-bc\\ & = & \frac{1}{2}\left[\left(a-b\right)^{2}+\left(b-c\right)^{2}+\left(c-a\right)^{2}\right]\\ & \geqslant & 0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c8ec6357c65e04288bdb6cb1daa4d3c_l3.png)
Exemple 3
Pour tout ![]() l’on pose :
l’on pose :
![]()
![]()
Ceci montre notamment que, pour ![]() réels :
réels :![]() avec égalité si, et seulement si, deux au moins des trois nombres
avec égalité si, et seulement si, deux au moins des trois nombres ![]() sont nuls.
sont nuls.
On entend généralement par identité remarquable une égalité faisant intervenir une ou plusieurs variable(s), qui est vraie pour toute(s) valeur(s) de la (des) variable(s).
Les exemples les plus célèbres sont certainement :
(1) ![]()
(2) ![]()
Cette vidéo aborde de manière élémentaire la question des identités remarquables.
La relation (1) se généralise en la formule du binôme :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\forall\left(a,b\right)\in\mathbb{C}^{2},\thinspace\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k}b^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f8b1ea977a5ed4d7480d6eb1a7f394d_l3.png)
La relation (2) se généralise sous la forme :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}-\left\{ 0,1\right\} ,\forall\left(a,b\right)\in\mathbb{C}^{2},\thinspace a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{n-k}b^{k-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c73bd46f1a641ab8979e76ae6d743ec6_l3.png)
Voici quelques identités remarquables, plus « exotiques » :
Exemple 1
Pour tout ![]() :
:
![]()
Exemple 2
Pour tout ![]() :
:
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*} \left(a+bj+cj^{2}\right)\left(a+bj^{2}+cj\right) & = & a^{2}+b^{2}+c^{2}-ab-ac-bc\\ & = & \frac{1}{2}\left[\left(a-b\right)^{2}+\left(b-c\right)^{2}+\left(c-a\right)^{2}\right]\\ & \geqslant & 0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c8ec6357c65e04288bdb6cb1daa4d3c_l3.png)
Exemple 3
Pour tout ![]() l’on pose :
l’on pose :
![]()
![]()
Ceci montre notamment que, pour ![]() réels :
réels :![]() avec égalité si, et seulement si, deux au moins des trois nombres
avec égalité si, et seulement si, deux au moins des trois nombres ![]() sont nuls.
sont nuls.
Exemple 4
Pour tout couple ![]() de réels positifs :
de réels positifs :
![]()
Elle fait aussi l’objet du challenge n° 67
INDICATRICE (fonction)
Etant donnés un ensemble ![]() et une partie
et une partie ![]() de
de ![]() , la fonction indicatrice de
, la fonction indicatrice de ![]() est l’application :
est l’application :
![]()
Exemples
Si ![]() est une partie finie d’un ensemble
est une partie finie d’un ensemble ![]() , alors
, alors
![]()
La fonction indicatrice de ![]() est une application discontinue en tout point.
est une application discontinue en tout point.
Si ![]() est un intervalle de
est un intervalle de ![]() , de longueur
, de longueur ![]() , alors
, alors ![]() est une densité de probabilité pour la loi uniforme sur
est une densité de probabilité pour la loi uniforme sur ![]() .
.
Si ![]() est un espace probabilisé et
est un espace probabilisé et ![]() un événement, la variable aléatoire indicatrice de
un événement, la variable aléatoire indicatrice de ![]() vérifie
vérifie ![]() .
.
INTÈGRE (anneau)
Définition
Un anneau ![]() est dit intègre s’il est non nul, commutatif et si de plus :
est dit intègre s’il est non nul, commutatif et si de plus :
![]()

Cette célèbre phrase, entendue dans les cours d’enseignement secondaire, exprime l’intégrité de l’anneau des nombres réels.
En fait, les nombres réels forment un corps et tout corps est un anneau intègre (mais la réciproque est fausse, comme on le voit avec l’anneau ![]() par exemple).
par exemple).
Comme exemples d’anneaux non intègres, citons :
- les anneaux quotients
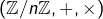 pour
pour 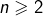 , non premier.
, non premier. - l’anneau
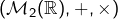 .
. - l’anneau des applications continues de
 dans
dans  .
.
On peut montrer que tout anneau intègre fini est un corps.
Pour un anneau commutatif ![]() , l’intégrité de
, l’intégrité de ![]() équivaut à celle de l’anneau de polynômes
équivaut à celle de l’anneau de polynômes ![]() .
.
Pour finir, signalons l’important :
Théorème
Pour tout anneau intègre ![]() , la relation
, la relation ![]() définie sur
définie sur ![]() par :
par :
![]()
On note ![]() la classe d’équivalence de
la classe d’équivalence de ![]() .
.
En posant :
![]()
En outre l’application ![]() est un morphisme injectif d’anneaux, ce qui permet d’identifier
est un morphisme injectif d’anneaux, ce qui permet d’identifier ![]() à un sous-anneau de
à un sous-anneau de ![]() .
.
![]() est appelé le corps des fractions de
est appelé le corps des fractions de ![]() . C’est ainsi que l’on construit
. C’est ainsi que l’on construit ![]() (corps des nombres rationnels) à partir de
(corps des nombres rationnels) à partir de ![]() (anneau des entiers) ou encore
(anneau des entiers) ou encore ![]() (corps des fractions rationnelles) à partir de
(corps des fractions rationnelles) à partir de ![]() (anneau des polynômes).
(anneau des polynômes).
INTERMÉDIAIRES (théorème des valeurs)
Si l’on considère un intervalle I non trivial ainsi qu’une application ![]() continue, alors
continue, alors ![]() est un intervalle (au sujet de la notation
est un intervalle (au sujet de la notation ![]() et de la notion d’image directe, voir cet article).
et de la notion d’image directe, voir cet article).
Ceci signifie que pour tout couple de réels atteints par ![]() chaque réel compris entre ces deux-là est aussi atteint par
chaque réel compris entre ces deux-là est aussi atteint par ![]() Un énoncé équivalent est le suivant :
Un énoncé équivalent est le suivant :
Théorème des valeurs intermédiaires
Si ![]() est un intervalle non trivial, si
est un intervalle non trivial, si ![]() est continue et s’il existe
est continue et s’il existe ![]() vérifiant
vérifiant ![]() alors il existe
alors il existe ![]() tel que
tel que ![]()
La condition ![]() signifie que les réels
signifie que les réels ![]() et
et ![]() sont non nuls et de signes contraires.
sont non nuls et de signes contraires.
Ce que dit ce théorème est assez intuitif : si par exemple la température est passée de +5°C hier soir à -2°C ce matin, alors il y a certainement eut un moment (ou plusieurs …), dans la nuit, où la température était exactement de 0°C. A condition bien sûr qu’on admette que la température varie « continûment » …
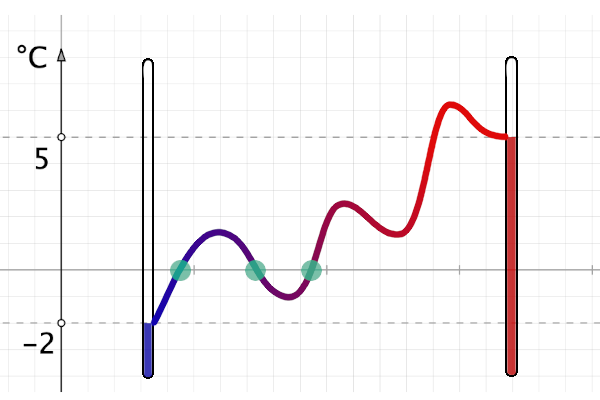
Une illustration amusante du TVI (théorème des valeurs intermédiaires) est la suivante : si un cycliste parcourt une distance de 20 km en 2 heures (selon un mouvement non supposé uniforme : il peut accélérer, ralentir, s’arrêter pour faire pipi …), alors il existe à coup sûr un intervalle de temps de 1 heure au cours duquel il a parcouru exactement 10 km.
Autre exemple : étant donné un cerceau métallique, chauffé de manière non supposée uniforme, il existe forcément deux points diamétralement opposés ou règne la même température.
Plus sérieusement, le TVI permet d’affirmer l’existence de solutions à certaines équations. Par exemple, l’application ![]() possède certainement un point fixe. En effet, l’équation
possède certainement un point fixe. En effet, l’équation ![]() équivaut à
équivaut à ![]() or l’application
or l’application ![]() est continue et prend des valeurs de signes opposés :
est continue et prend des valeurs de signes opposés :
![]()
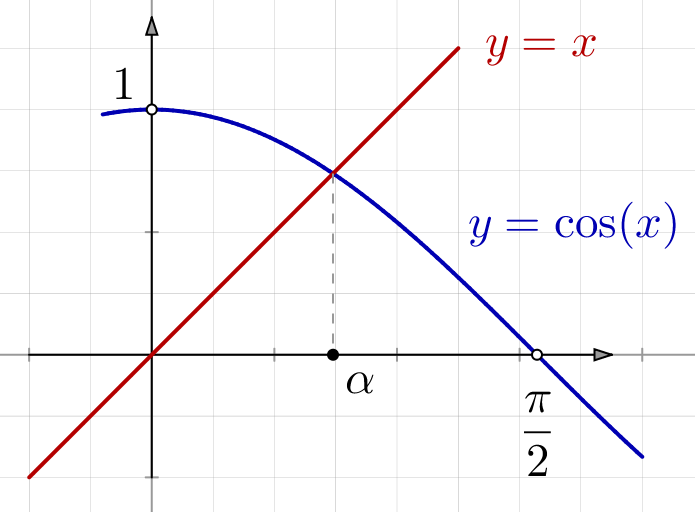
Il se trouve en outre que ![]() est strictement croissante (donc injective), ce qui fait de
est strictement croissante (donc injective), ce qui fait de ![]() l’unique point fixe de
l’unique point fixe de ![]()
A un niveau plus avancé, le TVI se généralise comme suit :
Théorème
Soient ![]() des espaces topologiques et
des espaces topologiques et ![]() une application continue. Si
une application continue. Si ![]() est une partie connexe de
est une partie connexe de ![]() alors
alors ![]() est une partie connexe de
est une partie connexe de ![]()
Il s’agit bien d’une généralisation, car les parties connexes de ![]() sont les intervalles.
sont les intervalles.
INTERVALLE
Définition
Un intervalle de ![]() est une partie
est une partie ![]() de
de ![]() vérifiant la condition :
vérifiant la condition :
![]()
On classe les intervalles en sous-catégories (ci-dessous, ![]() sont tels que
sont tels que ![]() :
:
- la partie vide :
![Rendered by QuickLaTeX.com \[\emptyset\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d6ba46edb8fb61f6691beaf5ce422172_l3.png)
- les singletons :
![Rendered by QuickLaTeX.com \[\left\{ a\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-62517c15bdf74d75f2aa37a44f78b55f_l3.png)
- les segments non triviaux :
![Rendered by QuickLaTeX.com \[\left[a,b\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09605dc258196800a69c7b347e2a9b5d_l3.png)
- les intervalles semi-ouverts bornés :
![Rendered by QuickLaTeX.com \[\left]a,b\right]\quad\text{ou bien}\quad\left[a,b\right[\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-697071dab4d10f27ba986169667b7b5a_l3.png)
- les intervalles ouverts bornés :
![Rendered by QuickLaTeX.com \[\left]a,b\right[\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-088b46652dba07f18ef7bbe334b95a65_l3.png)
- les intervalles ouverts non bornés autres que
 :
:![Rendered by QuickLaTeX.com \[\left]-\infty,a\right[\quad\text{ou bien}\quad\left]a,+\infty\right[\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b862f10e018efd32be26da6147e6959e_l3.png)
- les intervalles fermés non bornés autres que
 :
:![Rendered by QuickLaTeX.com \[\left]-\infty,a\right]\quad\text{ou bien}\quad\left[a,+\infty\right[\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a2e04f9524dd7d4c525fd7c392a0667_l3.png)

La longueur d’un intervalle borné non vide ![]() est :
est : ![]()
Par convention ![]() et
et ![]() si
si ![]() est non borné.
est non borné.
Un intervalle est qualifié de trivial s’il est vide ou réduit à un singleton. Cela revient à dire qu’il est de longueur nulle.
Les intervalles sont présents dans les énoncés d’importants théorèmes d’analyse réelle. Par exemple :
- Si
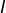 est un intervalle non trivial et
est un intervalle non trivial et 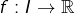 est continue et prend des valeurs positives et des valeurs négatives, alors
est continue et prend des valeurs positives et des valeurs négatives, alors  s’annule.
s’annule. - Si
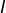 est un intervalle non trivial et si
est un intervalle non trivial et si 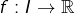 est continue et injective, alors
est continue et injective, alors  est strictement monotone.
est strictement monotone. - Si
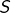 est un segment (non trivial) et
est un segment (non trivial) et 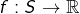 continue, alors
continue, alors  est bornée et atteint ses bornes.
est bornée et atteint ses bornes.
Remarque
La notion de segment peut-être étendue à un quelconque ![]() espace vectoriel
espace vectoriel ![]() Etant donnés deux vecteurs
Etant donnés deux vecteurs ![]() :
:
![]()
INVOLUTION
Définition
Etant donné un ensemble non vide ![]() on appelle involution de
on appelle involution de ![]() toute application
toute application ![]() vérifiant
vérifiant ![]()
Une telle application est nécessairement bijective.
Une involution est parfois appelée une symétrie (notamment en algèbre linéaire, lorsqu’il s’agit d’un endomorphisme involutif).
Exemple 1
Parmi les applications affines ![]() les involutions sont :
les involutions sont :
- d’une part
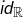 (qui correspond à
(qui correspond à 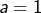 et
et 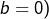
- et d’autre part celles associées à
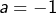 (et
(et 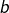 quelconque)
quelconque)
Exemple 2
L’application ![]() est une involution.
est une involution.
Exemple 3
La seule involution croissante de ![]() est
est ![]()
Exemple 4
Si ![]() est un
est un ![]() espace vectoriel de dimension finie et si
espace vectoriel de dimension finie et si ![]() est un endomorphisme involutif de
est un endomorphisme involutif de ![]() alors
alors ![]() est diagonalisable et
est diagonalisable et ![]() est un projecteur.
est un projecteur.
Exemple 5
Dans le groupe symétrique ![]() les transpositions sont des involutions mais ce ne sont pas les seules. Si l’on note
les transpositions sont des involutions mais ce ne sont pas les seules. Si l’on note ![]() le nombre d’involutions dans
le nombre d’involutions dans ![]() alors pour tout
alors pour tout ![]() :
:
![]()

