Lettre T
TELESCOPIQUE
Etant donnée une liste ![]() de nombres réels, la somme :
de nombres réels, la somme :
![Rendered by QuickLaTeX.com \[S=\sum_{k=1}^{n}\left(x_{k}-x_{k-1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-84cb1d3d22be1dc35eccf213abb2dd7b_l3.png)
![]()
Cette sommation est qualifiée de télescopique, car tout se passe comme si l’on repliait une longue vue d’autrefois … après coup, seuls l’oculaire et l’objectif sont encore visibles :

La raison de cette simplification est que les termes se simplifient de proche en proche, à l’exception des termes extrêmes, qui ne trouvent pas de contrepartie (illustration pour ![]() ) :
) :
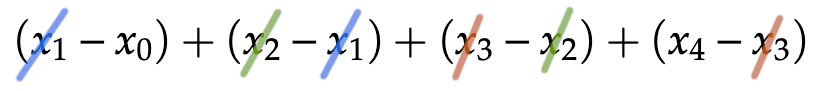
Pour une preuve rigoureuse, une petite récurrence fait l’affaire.
Cette technique est largement utilisée pour calculer explicitement
certaines sommes ou sommes de séries. Elle est aussi évoquée dans cet article, où vous pourrez trouver d’autres exemples que ceux développés ci-après.
Exemple 1
Si l’on pose 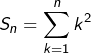 pour tout
pour tout ![]() alors la somme :
alors la somme :
![Rendered by QuickLaTeX.com \[T_{n}=\sum_{k=1}^{n}\left[\left(k+1\right)^{3}-k^{3}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a27c139b1f7f2e1d101e005d60cd991d_l3.png)
➢ D’une part :
![]()
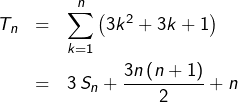
![]()
![Rendered by QuickLaTeX.com \[\boxed{S_{n}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d9cb5c0a498dbbb86c34194dd260a13c_l3.png)
Exemple 2
Calculons la somme de la série convergente :
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant2}\,\frac{F_{n}}{F_{n-1}\,F_{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec6ad9c0a3669d10e6d06d12cf6d2642_l3.png)
Pour tout ![]() :
:
![]()
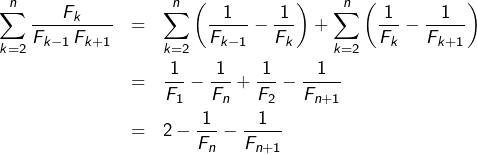
![Rendered by QuickLaTeX.com \[\boxed{\sum_{n=2}^{+\infty}\,\frac{F_{n}}{F_{n-1}\,F_{n+1}}=2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7dc7c7ea6ae1670d2e84cabd079401a9_l3.png)
Pour un autre exemple de calcul de somme de série faisant intervenir une sommation télescopique et les nombres de Fibonacci, voir l’exercice n° 5 de cette fiche.
Bien sûr, cette technique s’adapte aussi aux produits.
Si ![]() est une liste de réels non nuls, alors :
est une liste de réels non nuls, alors :
![Rendered by QuickLaTeX.com \[\prod_{k=1}^{n}\frac{y_{k}}{y_{k-1}}=\frac{y_{n}}{y_{0}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-87741d1b4a4ead38dab3d989920622ee_l3.png)
Exemple 3
Calculons explicitement, pour tout entier ![]() le produit :
le produit :
![Rendered by QuickLaTeX.com \[P_{n}=\prod_{k=2}^{n}\left(1-\frac{1}{k^{2}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-002757ed96d437fe651ca6489ca10b2e_l3.png)
![Rendered by QuickLaTeX.com \[P_{n}=\prod_{k=2}^{n}\frac{k^{2}-1}{k^{2}}=\prod_{k=2}^{n}\frac{\left(k-1\right)\left(k+1\right)}{k^{2}}=U_{n}V_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53c828975277e77e6edc442c1cb18d0c_l3.png)
![Rendered by QuickLaTeX.com \[U_{n}=\prod_{k=2}^{n}\frac{k-1}{k}\quad\text{et}\quad V_{n}=\prod_{k=2}^{n}\frac{k+1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2e19567dd542056c24952f8e731a5cd0_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{P_{n}=\frac{n+1}{2n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c7a4c4f44b4ddaf7c333ab2c4b57e128_l3.png)
![Rendered by QuickLaTeX.com \[\prod_{k=2}^{\infty}\left(1-\frac{1}{k^{2}}\right)=\frac{1}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9aae6ac2c872429c6c529ae6e2cd5018_l3.png)
TRANSITIVITÉ
La transitivité est une propriété que possèdent certaines relations binaires et que l’on pourrait bien caricaturer par le dicton populaire :
les amis de mes amis sont mes amis
Plus sérieusement, si ![]() est une relation binaire sur un ensemble
est une relation binaire sur un ensemble ![]() on dit que
on dit que ![]() est transitive lorsque :
est transitive lorsque :
![]()
Par exemple, les relations suivantes sont transitives :
- la relation d’égalité dans un ensemble quelconque,
- la relation d’inclusion dans l’ensemble des parties d’un ensemble,
- la relation
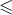 usuelle dans
usuelle dans 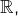
- la relation de divisibilité dans
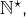
- l’ordre lexicographique (c’est-à-dire l’ordre usuel du dictionnaire) dans l’ensemble des mots sur un alphabet quelconque.
Voici maintenant un exemple de relation binaire non transitive : considérons l’ensemble des mots de la langue française. Etant donnés deux mots ![]() et
et ![]() on notera
on notera ![]() lorsque
lorsque ![]() et
et ![]() ont au moins une lettre en commun.
ont au moins une lettre en commun.
On voit bien que : bleu ![]() vert (le lettre ‘e’ est commune)
vert (le lettre ‘e’ est commune)
et vert ![]() roti (les lettres ‘r’ et ‘t’ sont communes)
roti (les lettres ‘r’ et ‘t’ sont communes)
mais bleu n’est pas en relation avec roti, car ces deux mots n’ont aucune lettre en commun.
Une question classique de combinatoire consiste à dénombrer les relations binaires sur un ensemble de cardinal ![]() (il en existe
(il en existe ![]() et à compter combien d’entre elles sont :
et à compter combien d’entre elles sont :
- réflexives : il en existe
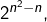
- symétriques : il en existe
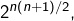
- réflexives, symétriques et transitives (relations d’équivalence) : il en existe
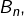 où
où 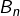 est le
est le 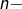 ème nombre de Bell. La suite
ème nombre de Bell. La suite 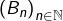 vérifie la relation de récurrence forte :
vérifie la relation de récurrence forte : ![Rendered by QuickLaTeX.com \[ B_{0}=1\qquad\text{et}\qquad\forall n\in\mathbb{N},\,B_{n+1}=\sum_{k=0}^{n}\,\binom{n}{k}B_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09aecac2804050afbb075318c75d0c15_l3.png)
A ce jour, aucune formule explicite n’est connue pour le nombre de relations transitives.
TRIANGULAIRE (inégalité)
Dans un triangle, la longueur de l’un quelconque des trois côtés est majorée par la somme des deux autres. Quitte à représenter chaque point du plan par son affixe (complexe), cette propriété s’énonce ainsi :
(![]() )
) ![]()
(![]() )
) ![]()
Détail de l’équivalence
En supposant ![]() on peut remplacer
on peut remplacer ![]() par
par ![]()
![]() par
par ![]() et
et ![]() par
par ![]() ce qui donne
ce qui donne ![]()
Réciproquement, en supposant ![]() on peut remplacer
on peut remplacer ![]() par
par ![]() et
et ![]() par
par ![]() ce qui donne
ce qui donne ![]()
La relation ![]() est appelée inégalité triangulaire dans
est appelée inégalité triangulaire dans ![]() En voici deux corollaires importants :
En voici deux corollaires importants :
![]()
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}-\left\{ 0,1\right\} ,\thinspace\forall\left(z_{1},\cdots,z_{n}\right)\in\mathbb{C}^{n},\thinspace\left|\sum_{k=1}^{n}z_{k}\right|\leqslant\sum_{k=1}^{n}\left|z_{k}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d7e74533b82017ffcfe35bc116c3ccb_l3.png)
On pourra consulter cette vidéo pour une preuve de ![]() et des deux corollaires, et cette autre pour des exemples d’utilisation.
et des deux corollaires, et cette autre pour des exemples d’utilisation.
Plus généralement, si ![]() est un
est un ![]() ou
ou ![]() -espace vectoriel et si
-espace vectoriel et si ![]() est une norme (ou même une semi-norme) sur
est une norme (ou même une semi-norme) sur ![]() , alors
, alors ![]() pour tout couple
pour tout couple ![]() de vecteurs de
de vecteurs de ![]()
Par exemple, si ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[\left(\int_{0}^{1}\left|f\left(t\right)+g\left(t\right)\right|^{p}\thinspace dt\right)^{1/p}\leqslant\left(\int_{0}^{1}\left|f\left(t\right)\right|^{p}\thinspace dt\right)^{1/p}+\left(\int_{0}^{1}\left|g\left(t\right)\right|^{p}\thinspace dt\right)^{1/p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9852f29a5ed64e37318b22fcb7286e42_l3.png)
![]()
TRIANGULAIRE (matrice)
Soit ![]() un entier naturel non nul et soit
un entier naturel non nul et soit ![]() un corps.
un corps.
Définition
Une matrice carrée ![]() est dite triangulaire supérieure lorsque ses termes sous-diagonaux sont tous nuls.
est dite triangulaire supérieure lorsque ses termes sous-diagonaux sont tous nuls.
En posant ![]() cette condition prend la forme :
cette condition prend la forme :
![]()
On dit qu’une matrice est triangulaire inférieure lorsque sa transposée est triangulaire supérieure. L’ensemble de ces matrices est noté ![]()
Exemple
La matrice :
![Rendered by QuickLaTeX.com \[\left[\begin{array}{ccccc}0 & 1 & 0 & -1 & \frac{1}{2}\\0 & 1 & 4 & 6 & 0\\0 & 0 & 2 & 9 & 1\\0 & 0 & 0 & e & -\frac{1}{3}\\0 & 0 & 0 & 0 & \pi\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-64eb169fb6198bfa1d8e7f342bfa063c_l3.png)
L’ensemble ![]() contient la matrice nulle et la matrice unité, est stable par combinaison linéaire et par produit. C’est donc une sous-algèbre de
contient la matrice nulle et la matrice unité, est stable par combinaison linéaire et par produit. C’est donc une sous-algèbre de ![]() Sa dimension est :
Sa dimension est :
![]()
Même chose pour ![]() via l’isomorphisme
via l’isomorphisme ![]()
Proposition 1
Une matrice triangulaire est inversible si, et seulement si, ses termes diagonaux sont tous non nuls.
Cette proposition se prouve directement.
Elle peut aussi être vue comme conséquence de la :
Proposition 2
Le déterminant d’une matrice triangulaire est égal au produit de ses termes diagonaux.
Plus généralement, le déterminant d’une matrice triangulaire par blocs est égal au produit des déterminants de ses blocs diagonaux.
Exemple
Après avoir calculé :
![Rendered by QuickLaTeX.com \[\left|\begin{array}{cc} 2 & -1\\ 1 & 2 \end{array}\right|=5\qquad\text{et}\qquad\left|\begin{array}{ccc} 2 & 1 & 1\\ 1 & 2 & 3\\ 0 & -1 & -4 \end{array}\right|=-7\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-981e2a6645b9761ccb06099dd8dbeab9_l3.png)
![Rendered by QuickLaTeX.com \[\left|\begin{array}{ccccc} 2 & -1 & 0 & 0 & 0\\ 1 & 2 & 0 & 0 & 0\\ 0 & 0 & 2 & 1 & 1\\ 0 & 0 & 1 & 2 & 3\\ 0 & 0 & 0 & -1 & -4 \end{array}\right|=-35 \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f7237ffbdc7eeacfabaa2892ec69588d_l3.png)
Proposition 3
Toute matrice triangulaire stricte (c’est-à-dire : dont les termes diagonaux sont tous nuls) est nilpotente.
Exemple
C’est en particulier le cas de la matrice suivante (cellule de Jordan de taille ![]() :
:
![Rendered by QuickLaTeX.com \[J_{n}=\left[\begin{array}{ccccc}0 & 1 & 0 & \cdots & 0\\0 & 0 & 1 & \ddots & \vdots\\\vdots & \ddots & \ddots & \ddots & 0\\\vdots & & \ddots & \ddots & 1\\0 & \cdots & \cdots & 0 & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1424329e72f2645673c4da3d20913c68_l3.png)
Proposition 4
Toute matrice ![]() dont le polynôme caractéristique est scindé dans
dont le polynôme caractéristique est scindé dans ![]() est semblable à une matrice triangulaire supérieure, c’est-à-dire qu’il existe
est semblable à une matrice triangulaire supérieure, c’est-à-dire qu’il existe ![]() et
et ![]() telles que :
telles que :
![]()
TRIANGULAIRE (nombre)
Les entiers :
![]()
L’illustration suivante explique l’origine de cette terminologie. On y voit un empilement de :
![]()

La formule suivante est archi-classique :
Proposition
Pour tout ![]() :
:
![]()
Il est intéressant de noter que si les deux membres de cette égalité représentent le même nombre, la quantité de calcul nécessaire n’est pas identique dans les deux cas (les formules n’ont pas la même complexité) : ![]() additions d’un côté et, de l’autre, une addition, une multiplication et une division par 2.
additions d’un côté et, de l’autre, une addition, une multiplication et une division par 2.
L’égalité se prouve aisément par récurrence. On peut aussi voir que :
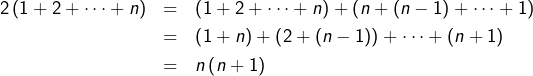
Les nombres triangulaires sont des nombres polygonaux particuliers. Le théorème de Fermat-Cauchy dit que, pour tout ![]() tout entier naturel est la somme d’au plus
tout entier naturel est la somme d’au plus ![]() nombres
nombres ![]() gonaux.
gonaux.
Le cas ![]() a été résolu par Lagrange en 1770 (c’est le théorème des quatre carrés). Le cas
a été résolu par Lagrange en 1770 (c’est le théorème des quatre carrés). Le cas ![]() a été résolu plus tard (en 1796) par Gauss. Le cas général est dû à Cauchy (1813). Quant à Fermat, il a formulé ce résultat en 1638, annoncé qu’il en publierait une preuve, ce qu’il n’a jamais fait.
a été résolu plus tard (en 1796) par Gauss. Le cas général est dû à Cauchy (1813). Quant à Fermat, il a formulé ce résultat en 1638, annoncé qu’il en publierait une preuve, ce qu’il n’a jamais fait.

