Solution pour le challenge n° 64

Solution pour le challenge 64

Notons :

$S=\sum_{1\leqslant i<j\leqslant n}\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)$

Le terme général de :

$E=\sum_{1\leqslant i,j\leqslant n}\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)$

dépend symétriquement du couple $\left(i,j\right)$ et vaut $0$ si $i=j.$ Par conséquent : $E=2S$ .

Par ailleurs, on obtient en développant :

$\begin{eqnarray*}E & = & \sum_{1\leqslant i,j\leqslant n}a_{j}b_{j}+\sum_{1\leqslant i,j\leqslant n}a_{i}b_{i}-\sum_{1\leqslant i,j\leqslant n}a_{j}b_{i}-\sum_{1\leqslant i,j\leqslant n}a_{i}b_{j}\\ & = & 2n\sum_{j=1}^{n}a_{j}b_{j}-2\left(\sum_{i=1}^{n}a_{i}\right)\left(\sum_{j=1}^{n}b_{j}\right) \end{eqnarray*}$

Il en résulte que :

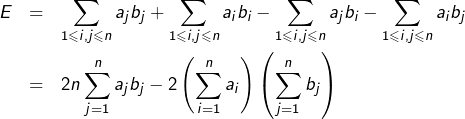
$\sum_{1\leqslant i<j\leqslant n}\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)=n\thinspace\sum_{j=1}^{n}a_{j}b_{j}-\left(\sum_{i=1}^{n}a_{i}\right)\left(\sum_{j=1}^{n}b_{j}\right)$

Le calcul ci-dessus est dû à J.M. Ferrard (cf. commentaire au bas de cette page).

Autre calcul, moins simple … (cliquer pour voir)

On développe, pour tout $\left(i,j\right)\in\left\llbracket 1,n\right\rrbracket ^{2}$ :
$\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)=a_{i}b_{i}+a_{j}b_{j}-a_{i}b_{j}-a_{j}b_{i}$
puis on somme :

$\begin{eqnarray*}&&\sum_{1\leqslant i<j\leqslant n}\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)\\&=&\sum_{1\leqslant i\leqslant j\leqslant n}\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)\\&=&\sum_{j=1}^{n}ja_{j}b_{j}+\sum_{i=1}^{n}\left(n+1-i\right)a_{i}b_{i}\\&&-\sum_{1\leqslant i\leqslant j\leqslant n}\left(a_{i}b_{j}+a_{j}b_{i}\right)\\&=&\left(n+1\right)\sum_{i=1}^{n}a_{i}b_{i}\\&&-\sum_{1\leqslant i\leqslant j\leqslant n}\left(a_{i}b_{j}+a_{j}b_{i}\right)\end{eqnarray*}$

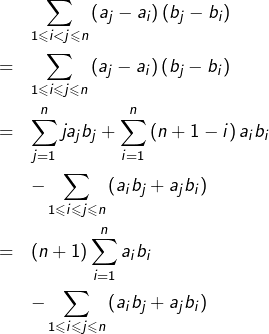
Or :

$\begin{eqnarray*}&&\sum_{1\leqslant i\leqslant j\leqslant n}\left(a_{i}b_{j}+a_{j}b_{i}\right)\\& = & \sum_{j=1}^{n}\left(\sum_{i=1}^{j}a_{i}\right)b_{j}\\&&+\sum_{i=1}^{n}\left(\sum_{j=i}^{n}a_{j}\right)b_{i}\\& = & \sum_{j=1}^{n}\left[\left(\sum_{i=1}^{j-1}a_{i}\right)+a_{j}\right]b_{j}\\&&+\sum_{j=1}^{n}\left(\sum_{i=j}^{n}a_{i}\right)b_{j}\\ & = & \sum_{j=1}^{n}a_{j}b_{j}+\left(\sum_{i=1}^{n}a_{i}\right)\left(\sum_{j=1}^{n}b_{j}\right) \end{eqnarray*}$

et donc, par différence :
$\displaystyle{\sum_{1\leqslant i<j\leqslant n}\left(a_{j}-a_{i}\right)\left(b_{j}-b_{i}\right)=n\thinspace\sum_{j=1}^{n}a_{j}b_{j}-\left(\sum_{i=1}^{n}a_{i}\right)\left(\sum_{j=1}^{n}b_{j}\right)}$

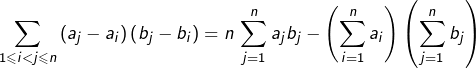
Si les listes $\left(a_{i}\right)_{1\leqslant i\leqslant n}$ et $\left(b_{i}\right)_{1\leqslant i\leqslant n}$ sont croissantes, alors le membre de gauche de l’égalité ci-dessus est positif ou nul, donc :

$\boxed{\left(\sum_{i=1}^{n}a_{i}\right)\left(\sum_{j=1}^{n}b_{j}\right)\leqslant n\sum_{j=1}^{n}a_{j}b_{j}}$

résultat connu sous le nom d’inégalité de Tchebytchev.

Considérons maintenant deux applications $f,g:\left[a,b\right]\rightarrow\mathbb{R}$ croissantes. Pour tout $n\in\mathbb{N}^{\star},$ posons :
$\displaystyle{x_{n,k}=a+\frac{k\left(b-a\right)}{n}\quad0\leqslant k\leqslant n}$
ainsi que :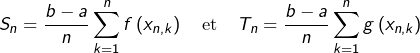
$\displaystyle{S_{n}=\frac{b-a}{n}\sum_{k=1}^{n}f\left(x_{n,k}\right)\quad\text{et}\quad T_{n}=\frac{b-a}{n}\sum_{k=1}^{n}g\left(x_{n,k}\right)}$

$S_{n}$ et $T_{n}$ sont des sommes de Riemann pour $f$ et à $g$ , associées à la subdivision régulière de pas $\frac{b-a}{n}.$

Les listes $\left(f\left(x_{n,k}\right)\right)_{1\leqslant k\leqslant n}$ et $\left(g\left(x_{n,k}\right)\right)_{1\leqslant k\leqslant n}$ étant croissantes, on voit en appliquant $\left(T\right)$ que :
$\displaystyle{\left(\sum_{k=1}^{n}f\left(x_{n,k}\right)\right)\left(\sum_{k=1}^{n}g\left(x_{n,k}\right)\right)\leqslant n\thinspace\sum_{k=1}^{n}f\left(x_{n,k}\right)g\left(x_{n,k}\right)}$

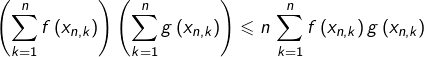
Après multiplication de chaque membre par $\frac{\left(b-a\right)^{2}}{n^{2}}$ , il en résulte :

( $\spadesuit$ ) $S_{n}T_{n}\leqslant\left(b-a\right)\thinspace P_{n}$

où l’on a posé :

$P_{n}=\frac{b-a}{n}\sum_{k=1}^{n}f\left(x_{n,k}\right)g\left(x_{n,k}\right)$

qui est une somme de Riemann attachée au produit $fg,$ toujours pour la même subdivision.

En passant à la limite lorsque $n\rightarrow+\infty$ dans $\left(\spadesuit\right)$ et d’après le théorème de convergence des sommes de Riemann :
$\boxed{\left(\int_{a}^{b}f\left(t\right)\thinspace dt\right)\left(\int_{a}^{b}g\left(t\right)\thinspace dt\right)\leqslant\left(b-a\right)\int_{a}^{b}f\left(t\right)g\left(t\right)\thinspace dt}$

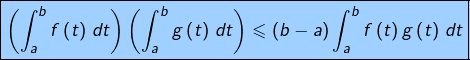
Pour consulter l’énoncé, c’est ici

Partager cet article

Cet article a 2 commentaires

René Adad 7 Juil 2021 Répondre

Merci pour ce commentaire qui rend effectivement la preuve plus simple ! J’ai inséré votre calcul dans le corps du texte.
jmf 7 Juil 2021 Répondre

Bonjour

Pour la première partie de la démonstration, il y a une preuve plus simple en remarquant que l’expression (aj-ai)(bj-bi) est symétrique en i,j, et qu’elle est nulle si i=j.

La double somme avec la condition i<j est donc la moitié de la somme sur le carré [1,n]x[1,n]. Et si on développe cette dernière on arrive immédiatement au résultat.

Cet article a 2 commentaires

Laisser un commentaire Annuler la réponse