Challenge 36 : Ecarts bornés … ou pas !

  • Auteur/autrice de la publication :
  • Post category:Challenge

icone-challenge-math-OS

On considère un nombre réel k\in\left]0,1\right[ et une application f:\mathbb{R}\rightarrow\mathbb{R} telle que, pour tout \left(x,y\right)\in\mathbb{R}^2 :

    \[\left|f\left(x\right)-f\left(y\right)\right|\leqslant k\left|x-y\right|\]

Etant donné s\in\mathbb{R} on définit deux suites \left(x_{n}\right)_{n\in\mathbb{N}} et \left(y_{n}\right)_{n\in\mathbb{N}} en posant :

  • x_{0}=y_{0}=s
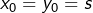
  • et pour tout n\in\mathbb{N} :

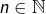    \[\left{ \begin{array}{ccc}x_{n+1} & = & f\left(x_{n}\right)\\\\y_{n+1} & = & \left\lfloor f\left(y_{n}\right)\right\rfloor\end{array}\right.\]

Le symbole \left\lfloor T\right\rfloor désigne la partie entière (par défaut) du réel T.

Montrer que la suite \left(x_{n}-y_{n}\right)_{n\in\mathbb{N}} est bornée.

Cette conclusion persiste-t-elle si l’on suppose k=1 ?

➥ Pour en savoir plus sur la fonction partie entière, on pourra consulter le lexique ou bien cette video.

Une solution est disponible ici

Partager cet article
    
Étiquettes : , , , , , , , , , , , , , , ,

Laisser un commentaire