
Dans l’article Qu’est-ce qu’une preuve par récurrence ?, la notion de démonstration par récurrence a été présentée dans son plus simple appareil et accompagnée de quelques exemples simples.
Pour l’essentiel, on y a expliqué qu’étant donnés un entier naturel ![]() et un énoncé
et un énoncé ![]() faisant intervenir un entier
faisant intervenir un entier ![]() il suffit pour montrer que
il suffit pour montrer que ![]() est vrai pour tout
est vrai pour tout ![]() d’établir deux choses :
d’établir deux choses :
➢ ![]() est vrai
est vrai
➢ Pour tout ![]() si
si ![]() est vrai, alors
est vrai, alors ![]() est aussi vrai.
est aussi vrai.
Ceci a été expliqué mais pas démontré…
Une preuve rigoureuse, lorsque ![]() , fait l’objet de la première section du présent article.
, fait l’objet de la première section du présent article.
Le cas général est analogue.
1 – Le principe de récurrence « classique »
On utilisera dans ce qui suit la propriété fondamentale suivante :
Proposition
Toute partie non vide de ![]() possède un plus petit élément.
possède un plus petit élément.
Considérons un énoncé ![]() portant sur un entier
portant sur un entier ![]() .
.
Supposons :
➣ d’une part, que ![]() est vrai (initialisation)
est vrai (initialisation)
➣ et d’autre part, que si ![]() est vrai pour un certain
est vrai pour un certain ![]() alors
alors ![]() est aussi vrai (hérédité).
est aussi vrai (hérédité).
Notons ![]() l’ensemble des entiers naturels
l’ensemble des entiers naturels ![]() pour lesquels
pour lesquels ![]() est vrai. On va établir, en raisonnant par l’absurde, que
est vrai. On va établir, en raisonnant par l’absurde, que ![]() ce qui signifiera exactement que
ce qui signifiera exactement que ![]() est vrai pour tout
est vrai pour tout ![]()
Supposons donc ![]() ce qui revient à dire que
ce qui revient à dire que ![]() (le complémentaire de
(le complémentaire de ![]() dans
dans ![]() est non vide. On peut alors considérer le plus petit élément de
est non vide. On peut alors considérer le plus petit élément de ![]() qu’on notera
qu’on notera ![]()
L’hypothèse ![]() montre que
montre que ![]() L’entier naturel
L’entier naturel ![]() n’appartient pas à
n’appartient pas à ![]() car il est inférieur au plus petit élément de cet ensemble; il appartient donc à
car il est inférieur au plus petit élément de cet ensemble; il appartient donc à ![]() et, vue l’hypothèse d’hérédité, son successeur
et, vue l’hypothèse d’hérédité, son successeur ![]() appartient aussi à
appartient aussi à ![]() Bref :
Bref : ![]() et
et ![]() ce qui est absurde.
ce qui est absurde.
On a bien prouvé que ![]() .
.
Aux exemples de preuves par récurrence présentés dans l’article Qu’est-ce qu’une preuve par récurrence, je propose d’ajouter le suivant, que je trouve particulièrement élégant.
2 – Pavage par des triminos
Recouvrir un damier de ![]() cases à l’aide de dominos (chaque domino recouvrant 2 cases) est une opération banale.
cases à l’aide de dominos (chaque domino recouvrant 2 cases) est une opération banale.
Et si l’on retire une case ? Cette opération est-elle encore possible ?
Evidemment non, puisqu’il reste un nombre impair de cases.
Ok. Et si l’on retire deux cases diagonalement opposées, le pavage redevient-il possible ?

Une astuce classique consiste à imaginer que les cases du damier ont été coloriées (blanches et noires, en alternance). Les deux cases supprimées étant de la même couleur, le nombre de cases blanches restantes est distinct du nombre de cases noires restantes ! Ceci montre l’impossibilité de la construction.

A présent, changeons complètement la règle du jeu : remplaçons les dominos par des « triminos », c’est-à-dire des pièces de la forme ci-contre.
Un trimino recouvre trois cases, disposées en ‘L’. On peut, en le faisant pivoter, le positionner de quatre manières.
Considérons un damier de format ![]() (avec
(avec ![]() qui comporte donc
qui comporte donc ![]() cases. Est-il possible de le recouvrir intégralement au moyen de triminos ?
cases. Est-il possible de le recouvrir intégralement au moyen de triminos ?
Il est clair que non, puisque ![]() n’est pas multiple de 3.
n’est pas multiple de 3.
Bon, d’accord… Et si l’on retire une case (peu importe laquelle) ? Cette fois l’argument arithmétique ne donne rien (au sens où aucune contradiction n’apparaît) car ![]() est multiple de
est multiple de ![]() .
.
Cette dernière affirmation peut se justifier d’au moins deux façons :
➢ Soit en raisonnant par récurrence : ![]() est un multiple de 3 (initialisation) et si
est un multiple de 3 (initialisation) et si ![]() avec
avec ![]() entier, alors
entier, alors ![]() est multiple de 3.
est multiple de 3.
➢ Soit en factorisant à l’aide de l’identité remarquable
![]()
![]()
Il s’avère que notre damier ![]() privé d’une case peut, quel que soit
privé d’une case peut, quel que soit ![]() et quelle que soit la case retirée, être recouvert par des triminos, ce que nous allons maintenant démontrer … par récurrence.
et quelle que soit la case retirée, être recouvert par des triminos, ce que nous allons maintenant démontrer … par récurrence.
L’initialisation est évidente : pour ![]() la zone est recouvrir a précisément la forme d’un trimino.
la zone est recouvrir a précisément la forme d’un trimino.
Supposons maintenant avoir réglé la question pour une certaine valeur de ![]() et considérons alors un damier de format
et considérons alors un damier de format ![]() privé d’un case.
privé d’un case.
Cette case (C) est contenue dans l’un des quatre sous-damiers de format ![]() : en haut à droite (HD), en haut à gauche (HG), en bas à droite (BD) ou en bas à gauche (BG). Pour fixer les idées (comme on dit), mettons qu’il s’agisse de (BG). Dans l’illustration ci-dessous, la case (C) est représentée en rouge.
: en haut à droite (HD), en haut à gauche (HG), en bas à droite (BD) ou en bas à gauche (BG). Pour fixer les idées (comme on dit), mettons qu’il s’agisse de (BG). Dans l’illustration ci-dessous, la case (C) est représentée en rouge.

En appliquant l’hypothèse de récurrence, on peut recouvrir (BG) privé de (C) :

Ensuite (astuce géniale !), on place un trimino au centre de la figure, de manière à occuper une case
de chacun des trois sous-damiers (HD), (HG) et (BD). Ce trimino est représenté ci-dessous en jaune :

Notons (C1), (C2) et (C3) ces trois cases. On peut appliquer l’hypothèse de récurrence :
➢ à (HD) privé de (C1)
➢ à (HG) privé de (C2)
➢ à (BD) privé de (C3)
et le tour est joué !

3 – Récurrences mal engagées
On tombe parfois sur des énoncés héréditaires, mais qui sont faux pour toutes les valeurs de ![]()
Le secret ? Un défaut d’initialisation !
Considérons par exemple l’énoncé ![]() suivant : « l’entier
suivant : « l’entier ![]() est multiple de
est multiple de ![]() « .
« .
Si l’on suppose ![]() vrai pour un certain
vrai pour un certain ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() et donc :
et donc :
![]()
Autrement dit
Mais il n’existe aucune valeur de
Le vice de forme est parfois mieux caché… Nous allons « démontrer » l’étonnant résultat suivant :
Etant donné un entier ![]() et
et ![]() points
points ![]() du plan, ces points sont nécessairement alignés.
du plan, ces points sont nécessairement alignés.
Manifestement, cette affirmation est vraie pour ![]() et pour
et pour ![]() Supposons-la vraie au rang
Supposons-la vraie au rang ![]() pour un certain
pour un certain ![]() et considérons
et considérons ![]() points
points ![]() On sait, par hypothèse de récurrence, que
On sait, par hypothèse de récurrence, que ![]() sont alignés et même chose pour
sont alignés et même chose pour ![]() Mais la droite qui porte les points
Mais la droite qui porte les points ![]() et celle qui porte
et celle qui porte ![]() sont nécessairement confondues, puisqu’elles ont en commun les points
sont nécessairement confondues, puisqu’elles ont en commun les points ![]() et
et ![]()
Pourtant, le résultat annoncé ne tient pas debout. Alors … où est l’erreur ?
La réponse à cette question est donnée en fin d’article 🙂
4 – Récurrences du second ordre
Principe
Considérons un énoncé ![]() portant sur un entier naturel
portant sur un entier naturel ![]() et supposons que :
et supposons que :
➡ ![]() et
et ![]() sont vrais,
sont vrais,
➡ Pour tout ![]() si
si ![]() et
et ![]() sont vrais alors
sont vrais alors ![]() est aussi vrai.
est aussi vrai.
Dans ces conditions, ![]() est vrai pour tout
est vrai pour tout ![]()
On peut aisément déduire ceci du principe de récurrence standard (cf. section 1), en appliquant ce dernier à l’énoncé ![]() suivant : «
suivant : « ![]() et
et ![]() sont vrais ». En effet :
sont vrais ». En effet :
➡ D’une part ![]() est vrai d’après l’hypothèse 1.
est vrai d’après l’hypothèse 1.
➡ D’autre part, si ![]() est vrai pour un certain
est vrai pour un certain ![]() cela signifie que
cela signifie que ![]() et
et ![]() sont vrais, donc (seconde hypothèse)
sont vrais, donc (seconde hypothèse) ![]() est vrai et donc
est vrai et donc ![]() aussi.
aussi.
Ainsi ![]() est vrai pour tout
est vrai pour tout ![]() ce qui prouve que
ce qui prouve que ![]() est vrai pour tout
est vrai pour tout ![]()
Examinons, dans les deux sections suivantes, quatre exemples d’utilisation.
5 – Deux exemples anecdotiques
Exemple 1
La suite de Fibonacci ![]() est définie par les relations :
est définie par les relations :
![]()
Vérifions que, pour tout ![]() :
:
![]()
Cette inégalité est clairement vérifiée aux rangs 0 et 1.
Supposons-la vraie aux rangs ![]() et
et ![]() pour un certain
pour un certain ![]() Alors :
Alors :
![]()
On pourra regarder l’exercice n° 2 de la fiche 01 sur la récurrence pour une minoration analogue de ![]()
Exemple 2
Posons pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[I_{n}=\int_{0}^{1}\frac{t^{n}}{\left(t+1\right)^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af7afcf66cf6654cafd41b579a42a842_l3.png)
![]()
Le calcul direct de ![]() n’ayant pas l’air évident, on commence par établir une relation de récurrence d’ordre
n’ayant pas l’air évident, on commence par établir une relation de récurrence d’ordre ![]() vérifiée par la suite
vérifiée par la suite ![]() L’idée est de se débarrasser du dénominateur en combinant trois termes consécutifs de cette suite. Pour tout
L’idée est de se débarrasser du dénominateur en combinant trois termes consécutifs de cette suite. Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\frac{t^{n+2}+2t^{n+1}+t^{n}}{\left(t+1\right)^{2}}=\frac{t^{n}\left(t^{2}+2t+1\right)}{\left(t+1\right)^{2}}=t^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-442e3314384ef34a5186a9b7ad86a492_l3.png)
![]()
Venons-en à la propriété annoncée dans l’encadré. On constate que :
![Rendered by QuickLaTeX.com \[I_{0}=\int_{0}^{1}\,\frac{1}{\left(t+1\right)^{2}}\,dt=\left[-\frac{1}{t+1}\right]_{0}^{1}=1-\frac{1}{2};\mbox{ soit : }\boxed{I_{0}=\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e498b8363b73ae764d6b3e6057434f3_l3.png)
![Rendered by QuickLaTeX.com \[I_{1}=\int_{0}^{1}\,\frac{t}{\left(t+1\right)^{2}}\,dt=\int_{0}^{1}\,\frac{\left(t+1\right)-1}{\left(t+1\right)^{2}}\,dt=\int_{0}^{1}\,\frac{1}{t+1}\,dt-I_{0};\mbox{ soit : }\boxed{I_{1}=\ln\left(2\right)-\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fd9f39c4a0d608975b2cee9e396f19d1_l3.png)
Alors, d’après ![]() , il en va de même pour
, il en va de même pour ![]() :
:
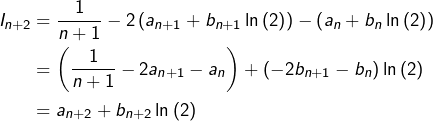
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{ccc}a_{n+2} & = & \frac{1}{n+1}-2a_{n+1}-a_{n}\in\mathbb{Q}\\\\b_{n+2} & = & -2b_{n+1}-b_{n}\in\mathbb{Q}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f46fe8c270775f16d8434459e10a969b_l3.png)
Remarque
La preuve par récurrence qui précède ne constitue pas la seule façon d’atteindre la conclusion. Si l’on sait décomposer une fraction rationnelle en éléments simples, on écrit pour tout ![]() :
:
![]()
Ceci donne aussitôt la réponse, après intégration sur
6 – Deux exemples plus sérieux
Exemple A
Considérons deux nombres réels ![]() tels que
tels que ![]() et soient
et soient ![]() les solutions (réelles) de l’équation du second degré
les solutions (réelles) de l’équation du second degré ![]() On sait que
On sait que ![]() On définit une famille de suites réelles par la relation de récurrence :
On définit une famille de suites réelles par la relation de récurrence :
![]()
La donnée des deux premiers termes ![]() et
et ![]() identifie alors une suite réelle et une seule. Comment exprimer
identifie alors une suite réelle et une seule. Comment exprimer ![]() de manière explicite en fonction de
de manière explicite en fonction de ![]()
![]() et
et ![]() pour tout
pour tout ![]() ?
?
Avec un peu d’algèbre linéaire, on peut parvenir de façon « naturelle » à cet objectif. Mais nous allons couper court et démontrer de façon rapide qu’il existe des réels ![]() tels que, pour tout
tels que, pour tout ![]() :
:
![]()
On commence par déterminer ![]() et
et ![]() de telle sorte que l’égalité ci-dessus soit vraie aux rangs 0 et 1, autrement dit que :
de telle sorte que l’égalité ci-dessus soit vraie aux rangs 0 et 1, autrement dit que :
![]()
![]()
Désormais, ![]() et
et ![]() étant ainsi définis, on suppose que pour un certain
étant ainsi définis, on suppose que pour un certain ![]() :
:
![]()
![]()
![]()
Mais on ne perd pas de vue que ![]() sont solutions de l’équation
sont solutions de l’équation ![]() ce qui permet de remplacer dans l’expression précédente
ce qui permet de remplacer dans l’expression précédente ![]() par
par ![]() et, de même,
et, de même, ![]() par
par ![]()
Au final :
![]()
Remarque
En appliquant ce qui précède à la célèbre suite de Fibonacci (voir au début de la section 5 pour sa définition), on voit qu’il existe des réels ![]() tels que :
tels que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace F_{n}=\lambda\left(\frac{1+\sqrt{5}}{2}\right)^{n}+\mu\left(\frac{1-\sqrt{5}}{2}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5bf3c129fe4a70a1e6616cc17afe5cb2_l3.png)
Comme ![]() et
et ![]() on vérifie (en résolvant donc un petit système) que :
on vérifie (en résolvant donc un petit système) que :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N},\:F_{n}=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5dcf98fc7945bcfe2df4da85e015a84_l3.png)
Exemple B
Les célèbres « polynômes de Tchebytchev » (de première espèce) peuvent être mis en évidence via une récurrence du second ordre.
Prouvons qu’il existe, pour chaque ![]() une unique fonction polynôme
une unique fonction polynôme ![]() à coefficients entiers telle que :
à coefficients entiers telle que :
![]()
Traitons d’emblée la question de l’unicité.
S’il existe, pour un certain ![]() deux fonctions polynômes
deux fonctions polynômes ![]() et
et ![]() vérifiant :
vérifiant :
![]()
![]()
Pour l’existence, on raisonne par récurrence.
Aucun problème pour les rangs 0 et 1; il est évident que ![]() et
et ![]() conviennent.
conviennent.
Supposons, pour un certain ![]() l’existence de fonctions polynômes à coefficients entiers
l’existence de fonctions polynômes à coefficients entiers ![]() et
et ![]() vérifiant la propriété. Alors, pour tout
vérifiant la propriété. Alors, pour tout ![]() :
:
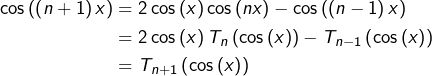
Manifestement ![]() est encore polynomiale et à coefficients entiers.
est encore polynomiale et à coefficients entiers.
Voir l’exercice n° 6 de la fiche 01 sur la récurrence pour un résultat analogue (polynômes de Tchebytchev de deuxième espèce).
7 – Récurrences finies
Proposition
Considérons un entier ![]() ainsi qu’un énoncé
ainsi qu’un énoncé ![]() portant sur un entier naturel
portant sur un entier naturel ![]() Supposons que :
Supposons que :
➡ ![]() est vrai,
est vrai,
➡ Pour tout ![]() si
si ![]() est vrai, alors
est vrai, alors ![]() est aussi vrai.
est aussi vrai.
Dans ces conditions, ![]() est vrai pour tout
est vrai pour tout ![]() .
.
Voici un exemple d’utilisation.
Inégalité de type Bernoulli
Un cas particulier de la très classique inégalité de Bernoulli (voir l’exercice n° 2 de la fiche récurrence – 01), nous dit que si ![]() sont deux entiers tels que
sont deux entiers tels que ![]() et
et ![]() alors :
alors :
![]()
On va montrer ici que si ![]() alors :
alors :
![]()
Pour cela, fixons ![]() et effectuons une récurrence (finie) sur
et effectuons une récurrence (finie) sur ![]()
Pour ![]() c’est clair ! Et si l’inégalité est vraie pour un certain entier
c’est clair ! Et si l’inégalité est vraie pour un certain entier ![]() tel que
tel que ![]() alors :
alors :
![]()
![]()
![]()
8 – Récurrences fortes
Principe
Considérons un énoncé ![]() portant sur un entier naturel
portant sur un entier naturel ![]() et supposons que :
et supposons que :
➡ ![]() est vrai,
est vrai,
➡ Pour tout ![]() si
si ![]() est vrai pour tout
est vrai pour tout ![]() alors
alors ![]() est aussi vrai.
est aussi vrai.
Dans ces conditions, ![]() est vrai pour tout
est vrai pour tout ![]()
Tout comme pour les récurrences du second ordre, ceci découle du principe de récurrence standard, appliqué à l’énoncé ![]() suivant : «
suivant : « ![]() est vrai pour tout
est vrai pour tout ![]() « .
« .
Un exemple à la fois simple et fondamental de récurrence forte ? La preuve de l’existence de diviseurs premiers.
De façon précise, on prouve que tout entier ![]() possède au moins un diviseur premier. C’est bien le cas pour
possède au moins un diviseur premier. C’est bien le cas pour ![]() (initialisation).
(initialisation).
Pour l’hérédité, on suppose que pour un certain ![]() et pour tout
et pour tout ![]() l’entier
l’entier ![]() possède au moins un diviseur premier. On s’intéresse alors à
possède au moins un diviseur premier. On s’intéresse alors à ![]() : si cet entier est premier, c’est réglé et sinon il possède un diviseur
: si cet entier est premier, c’est réglé et sinon il possède un diviseur ![]() tel que
tel que ![]() L’hypothèse de récurrence montre que
L’hypothèse de récurrence montre que ![]() possède un diviseur premier et donc
possède un diviseur premier et donc ![]() aussi.
aussi.
Dans les deux sections qui suivent, deux exemples beaucoup moins immédiats sont décortiqués.
9 – Nombres harmoniques
Dans ce qui suit, on note ![]() le
le ![]() ème nombre harmonique, défini par :
ème nombre harmonique, défini par :
![]()
Autrement dit, ![]() est la
est la ![]() ème somme partielle de la série harmonique.
ème somme partielle de la série harmonique.
Le calcul des premiers termes de la suite ![]() conduit à :
conduit à :
![]()
![]()
Toutes ces fractions sont écrites sous forme irréductible. Il semble que la suite des numérateurs augmente rapidement, tout comme celle des dénominateurs.
On peut montrer que la suite ![]() diverge vers
diverge vers ![]() et, plus précisément, que :
et, plus précisément, que :
![]()
![]()
On va plutôt soulever une question de nature arithmétique :
Question
Les nombres ![]() sont évidemment tous rationnels.
sont évidemment tous rationnels.
Mais certains d’entre-eux sont-ils entiers ?
Nous allons voir qu’à l’exception de ![]() (qui vaut
(qui vaut ![]() aucun terme de cette suite n’est entier.
aucun terme de cette suite n’est entier.
Voici l’angle d’attaque proposé :
Etant donnés deux entiers naturels non nuls ![]() et
et ![]() , on ne peut pas décider si le nombre rationnel
, on ne peut pas décider si le nombre rationnel ![]() est entier ou non, en connaissant seulement les parités de
est entier ou non, en connaissant seulement les parités de ![]() et de
et de ![]() … sauf dans un cas : celui où
… sauf dans un cas : celui où ![]() est impair et
est impair et ![]() est pair (auquel cas
est pair (auquel cas ![]() n’est pas entier).
n’est pas entier).
On va montrer que, pour tout ![]() le
le ![]() ème nombre harmonique
ème nombre harmonique ![]() peut s’écrire :
peut s’écrire :
![]()
Visiblement : ![]() est de cette forme.
est de cette forme.
Supposons (HR) que, pour tout entier ![]() tel que
tel que ![]() on ait :
on ait :
![]()
Alors :
![]()
Et si ![]() est pair, alors on observe, en posant
est pair, alors on observe, en posant ![]() que :
que :
![]()
![]()
Le rationnel ![]() est de la forme
est de la forme ![]() avec
avec ![]() impair (on le voit en réduisant au même dénominateur). Par ailleurs, d’après l’hypothèse de récurrence, on peut écrire :
impair (on le voit en réduisant au même dénominateur). Par ailleurs, d’après l’hypothèse de récurrence, on peut écrire :
![]()
![]()
10 – Une récurrence… à l’envers !
L’inégalité entre moyennes arithmétique et géométrique est un résultat important, qui fait partie du cortège des inégalités dites « usuelles ».
Théorème
Soit ![]() un entier supérieur ou égal à 2.
un entier supérieur ou égal à 2.
Pour tout ![]() uplet
uplet ![]() de réels strictement positifs :
de réels strictement positifs :
![]()
Dans le cas particulier où ![]() ce théorème dit que si
ce théorème dit que si ![]() et
et ![]() alors :
alors :
![]()
Pour ![]() quelconque, on voit généralement cette inégalité comme conséquence de la convexité de la fonction exponentielle (pour les détails, voir à la fin de cette section). Mais historiquement, ce n’est pas ainsi que la première démonstration a été obtenue.
quelconque, on voit généralement cette inégalité comme conséquence de la convexité de la fonction exponentielle (pour les détails, voir à la fin de cette section). Mais historiquement, ce n’est pas ainsi que la première démonstration a été obtenue.
On doit à Cauchy une très jolie preuve qui fonctionne un peu comme une récurrence, mais à l’envers. Elle repose sur le principe suivant :
Principe
On considère un énoncé ![]() satisfaisant aux deux hypothèses suivantes :
satisfaisant aux deux hypothèses suivantes :
➡ pour tout ![]() si
si ![]() est vrai alors
est vrai alors ![]() est aussi vrai,
est aussi vrai,
➡ il existe une suite ![]() d’entiers naturels :
d’entiers naturels :
- qui diverge vers
- telle que
 est vrai pour tout
est vrai pour tout 
Dans ces conditions, ![]() est vrai pour tout
est vrai pour tout ![]()
Le premier point justifie que l’on parle ici de récurrence à l’envers. Bien entendu, ce premier point est insuffisant, à lui seul, pour atteindre la conclusion.
Mais l’association des deux hypothèses fonctionne à merveille ! Intuitivement, pour prouver que ![]() est vrai pour un certain
est vrai pour un certain ![]() on va d’abord invoquer le second point et trouver un entier
on va d’abord invoquer le second point et trouver un entier ![]() tel que
tel que ![]() soit vrai; puis, grâce au premier point, « redescendre » de
soit vrai; puis, grâce au premier point, « redescendre » de ![]() à
à ![]() (en
(en ![]() itérations).
itérations).
La première étape consiste donc à vérifier que si l’inégalité ![]() est vraie au rang
est vraie au rang ![]() alors elle est aussi vraie au rang
alors elle est aussi vraie au rang ![]()
Et la seconde consistera ensuite à montrer que ![]() est vraie au rang
est vraie au rang ![]() pour tout
pour tout ![]() (autrement dit, la suite
(autrement dit, la suite ![]() utilisée sera la suite géométrique
utilisée sera la suite géométrique ![]()
Etape 1 (cliquer pour déplier / replier)
On suppose ici que, pour un certain ![]() et pour tout
et pour tout ![]() uplet
uplet ![]() de réels strictement positifs :
de réels strictement positifs :
![]()
Soient alors ![]() L’astuce consiste à écrire la moyenne géométrique de ces
L’astuce consiste à écrire la moyenne géométrique de ces ![]() réels comme celle de
réels comme celle de ![]() réels et d’appliquer l’hypothèse. Or justement, en raison de l’égalité :
réels et d’appliquer l’hypothèse. Or justement, en raison de l’égalité :
![]()
![]()
![]()
![]()
Etape 2 (cliquer pour déplier / replier)
On prouve ici, par une récurrence « standard », que pour tout ![]() :
:
![]()
![]()
Supposons l’inégalité ![]() établie au rang
établie au rang ![]() et soit
et soit ![]() une séquence de
une séquence de ![]() réels strictement positifs. On observe que :
réels strictement positifs. On observe que :
![]()
![]()
![]()
![]()
Ainsi :
![]()
Une preuve plus simple (cliquer pour déplier / replier)
Terminons cette section en donnant une preuve plus directe (ou moins alambiquée, comme on voudra), qui repose sur la convexité de la fonction exponentielle.
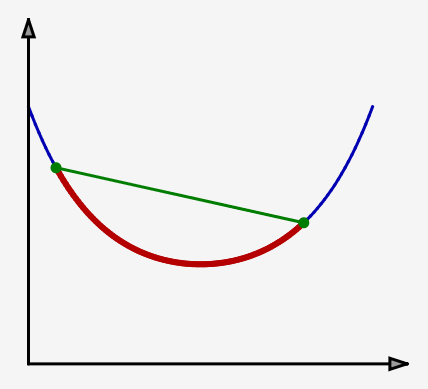
Rappelons qu’une fonction ![]() définie sur un intervalle
définie sur un intervalle ![]() et à valeurs dans
et à valeurs dans ![]() est dite convexe lorsque « toute portion de son graphe est située en-dessous de la corde correspondante », comme on le comprend sur l’illustration ci-contre.
est dite convexe lorsque « toute portion de son graphe est située en-dessous de la corde correspondante », comme on le comprend sur l’illustration ci-contre.
La version formalisée de cette définition est :
![]()
On peut montrer que si ![]() est dérivable, alors sa convexité équivaut à la croissance de sa dérivée (et il en résulte aussitôt que, pour
est dérivable, alors sa convexité équivaut à la croissance de sa dérivée (et il en résulte aussitôt que, pour ![]() deux fois dérivable, la convexité de
deux fois dérivable, la convexité de ![]() équivaut à la positivité de sa dérivée seconde).
équivaut à la positivité de sa dérivée seconde).
Enfin, si ![]() est convexe, alors (inégalité de Jensen discrète) pour tout entier
est convexe, alors (inégalité de Jensen discrète) pour tout entier ![]() pour tout
pour tout ![]() tel que
tel que ![]() et pour tout
et pour tout ![]() :
:
![]()
Ces généralités étant rappelées, et vu que la fonction exponentielle est convexe, on a pour tout ![]() et pour tout
et pour tout ![]() uplet
uplet ![]() de réels strictement positifs :
de réels strictement positifs :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\left(x_{1}\cdots x_{n}\right)^{1/n}\leqslant\frac{1}{n}\left(x_{1}+\cdots+x_{n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bf3d4424a2cd11de53df238232474919_l3.png)
L’inégalité voulue est ainsi établie.
11 – Retour sur un raisonnement invalide
A la section 3, nous avons présenté un résultat manifestement faux.
L’erreur résidait dans le fait que si ![]() les points
les points ![]() et
et ![]() sont confondus et ne définissent donc pas une droite !
sont confondus et ne définissent donc pas une droite !
Pour que cette prétendue preuve soit valide, encore eut-il fallu que l’on puisse initialiser la récurrence avec ![]() c’est qui est bien entendu impossible (on sait bien que trois points quelconques du plan ne sont en général pas alignés).
c’est qui est bien entendu impossible (on sait bien que trois points quelconques du plan ne sont en général pas alignés).
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Ça ne passe toujours pas. L’exercice illustratif (qui utilise une récurrence descendante forte) concernait la fonction de 91 de Mac Carthy que l’on trouve par exemple sur Wikipedia 🙂
***Quelques mots ne sont pas passés ! Je remets le paragraphe sans omission:
– Une variante parfois utile est la récurrence descendante: si E(N) est vrai, et si E(n) vrai entraîne E(n-1) vrai pour tout n entier relatif <=N, alors E(n) est vrai pour tout n entier relatif 100, et f(f(n+11)) pour n<=100, montrer que pour tout n<=101: f(n)=91.
Bonjour Monsieur,
Merci pour cet article généreux 🙂
Quelques petites remarques de forme:
-Partie 2: au début, dans la marge de droite, la figure présentant un trimino ne s’affiche pas;
-Partie 7: la phrase « dans ces conditions… » qui suit la proposition devait probablement être incluse dans l’encadré de couleur matérialisant la proposition;
-Partie 7: un peu plus bas, le lien renvoyant vers la fiche récurrence ne semble plus actif;
-Partie 10: dans la deuxième flèche du principe, il est possible d’ajouter que la suite (u(n)) est constituée d’entiers naturels « supérieurs ou égaux à 2 » afin que l’énoncé Eu(n) ait toujours un sens.
Quelques commentaires pour les autres lecteurs intéressés, ou vous-même si vous souhaitez rebondir sur certains d’entre eux:
-La récurrence du second ordre a été présentée dans la partie 4. On peut également utiliser des récurrences de tout ordre k supérieur ou égal à 3. Par exemple pour le cas du troisième ordre et pour des énoncés E(n) sur les entiers naturels n, l’initialisation consistera à montrer que E(0) E(1) et E(2) sont vrais, tandis que pour l’hérédité il faudra montrer que E(n) E(n+1) et E(n+2) vrais entraînent E(n+3) vrai;
-La démonstration de l’exemple A de la partie 6 qui fournit l’existence de lambda et mu, assure également l’unicité de ces deux réels;
-Une variante parfois utile est la récurrence descendante: si E(N) vrai, et si E(n) vrai entraîne E(n-1) vrai pour tout n entier relatif <=N, alors E(n) est vrai pour tout n entier relatif 100, et f(f(n+11)) pour n<=100, montrer que pour tout n<=101 on a f(n)=91;
-La récursivité, notion très utilisée en informatique, fait penser au raisonnement par récurrence;
-J'ai aperçu dans un devoir de prépa des "définitions et démonstrations par induction structurelle", et cela avait l'air proche de la notion de récurrence et intéressant ! ;
-Dans le même genre que le point précédent, toujours dans un devoir de prépa, il était présenté la notion de "récurrence transfinie sur un ensemble bien ordonné".
Enfin, si vous le voulez bien, plus tard lorsque vous aurez le temps pour cela, je me permets d’insister sur mon dernier commentaire présent à la suite de l'article « Négation, contraposée, réciproque », car je sens que vous aurez certainement des livres de qualité à conseiller aux lecteurs du site !
Bien à vous