1 – Une question de parité
Tout le monde sait ce qu’est un nombre pair : il s’agit tout simplement du double d’un nombre entier.
Par exemple, 1450 est pair puisque 1450 = 2 ![]() 725.
725.
Un nombre entier non pair est dit impair. On peut l’écrire sous la forme ![]() , où
, où ![]() est entier. Détaillons cette dernière affirmation :
est entier. Détaillons cette dernière affirmation :
Si ![]() est un entier impair, notons
est un entier impair, notons ![]() le plus grand entier pair inférieur à
le plus grand entier pair inférieur à ![]()
On constate que ![]() Il en résulte que
Il en résulte que ![]()
Il est facile de voir que la somme de deux entiers pairs ![]() et
et ![]() est encore un entier pair. En effet, en notant
est encore un entier pair. En effet, en notant ![]() et
et ![]() il vient
il vient ![]() Et comme
Et comme ![]() est entier (c’est la somme de deux entiers), alors
est entier (c’est la somme de deux entiers), alors ![]() est pair.
est pair.
Enonçons une règle plus générale :
Parité de la somme de deux entiers
Etant donnés deux entiers ![]() et
et ![]() deux cas se présentent :
deux cas se présentent :
- Si
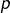 et
et 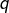 sont de même parité (tous deux pairs, ou bien tous
sont de même parité (tous deux pairs, ou bien tous
deux impairs), alors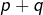 est pair.
est pair. - Si
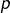 et
et 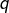 sont de parités contraires, alors
sont de parités contraires, alors 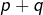 est impair.
est impair.
Le lecteur est invité à établir ce résultat, en exercice.
A présent, posons-nous la question suivante :
Question :
Etant donné un entier naturel ![]() quelle est la parité de
quelle est la parité de ![]() ?
?
Notons ![]() et regardons ce qui se passe pour les petites valeurs de
et regardons ce qui se passe pour les petites valeurs de ![]()
De simples calculs révèlent que :
![]()
![]()
On conjecture aussitôt que ![]() est impair, quel que soit
est impair, quel que soit ![]() ce qui est facile à établir directement ! On peut en effet écrire, pour tout
ce qui est facile à établir directement ! On peut en effet écrire, pour tout ![]() :
:
![]()
Et d’autre part, l’entier ![]() est évidemment impair.
est évidemment impair.
Ainsi ![]() est impair, puisque c’est la somme de deux entiers de parités contraires.
est impair, puisque c’est la somme de deux entiers de parités contraires.
Notre conjecture est devenue un théorème. Un théorème bien modeste, certes, mais que nous reprendrons à la section 4, en guise d’exemple de preuve par récurrence.
2 – Fausses Impressions
L’examen des quelques premières valeurs de ![]() pouvait-il suffire à nous convaincre de la validité de notre précédente conjecture ? La réponse est non, comme le prouvent les deux exemples suivants.
pouvait-il suffire à nous convaincre de la validité de notre précédente conjecture ? La réponse est non, comme le prouvent les deux exemples suivants.
Exemple 1
Pour tout entier ![]() notons
notons ![]() l’entier naturel dont l’écriture décimale comporte
l’entier naturel dont l’écriture décimale comporte ![]() chiffres ‘3’ suivis d’un ‘1’. Ainsi :
chiffres ‘3’ suivis d’un ‘1’. Ainsi :
![]()
![]() est-il toujours un nombre premier ?
est-il toujours un nombre premier ?
On constate que ![]()
![]()
![]()
![]()
![]()
![]() et
et ![]() sont tous premiers. Les quelques premières valeurs de
sont tous premiers. Les quelques premières valeurs de ![]() nous mettent donc sur la piste d’un « oui » !
nous mettent donc sur la piste d’un « oui » !
![]()
Et pour en savoir davantage sur les nombres premiers, on pourra consulter l’article Mysterieux nombres premiers.
Exemple 2
Etant donné un entier ![]() plaçons
plaçons ![]() points distincts sur un cercle et relions chacun d’eux à tous les autres. Ceci fait apparaître plusieurs régions à l’intérieur du disque : on notera
points distincts sur un cercle et relions chacun d’eux à tous les autres. Ceci fait apparaître plusieurs régions à l’intérieur du disque : on notera ![]() leur nombre. La question naturelle est : existe-t-il une formule simple pour
leur nombre. La question naturelle est : existe-t-il une formule simple pour ![]() ?
?
Notons, avant d’aller plus loin qu’il n’est du tout clair, a priori, que le nombre de régions dépende seulement de ![]() : cet entier pourrait très bien dépendre de la configuration choisie… mais passons.
: cet entier pourrait très bien dépendre de la configuration choisie… mais passons.
Effectuons la construction décrite plus haut pour les valeurs de n comprises entre 2 et 5 :
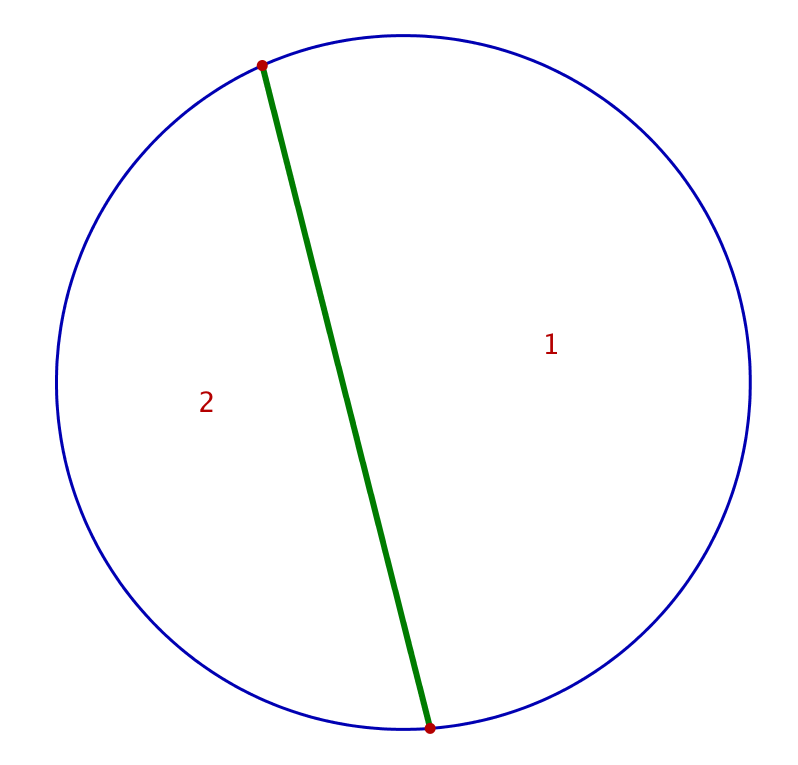
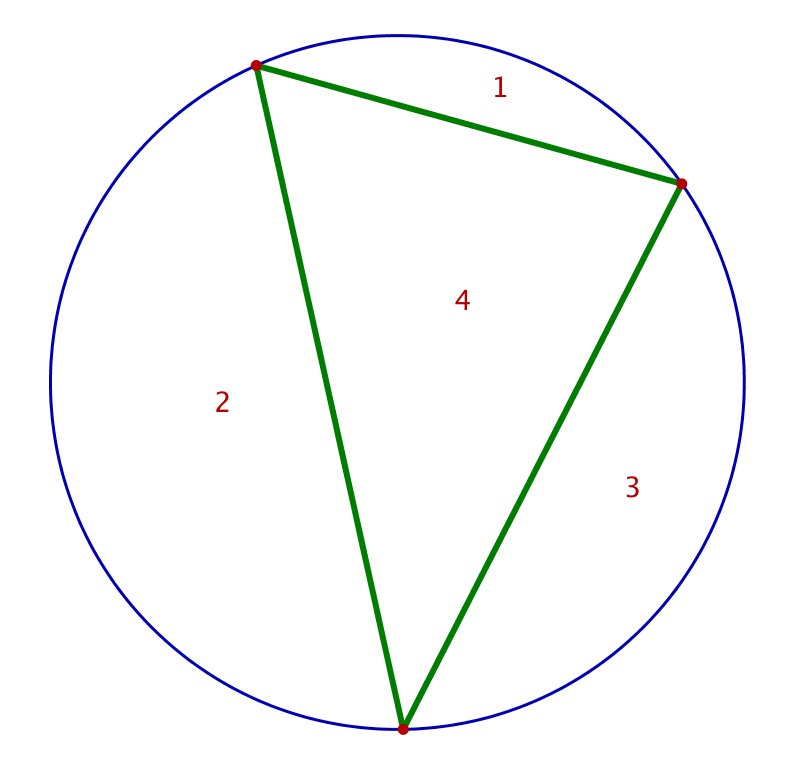
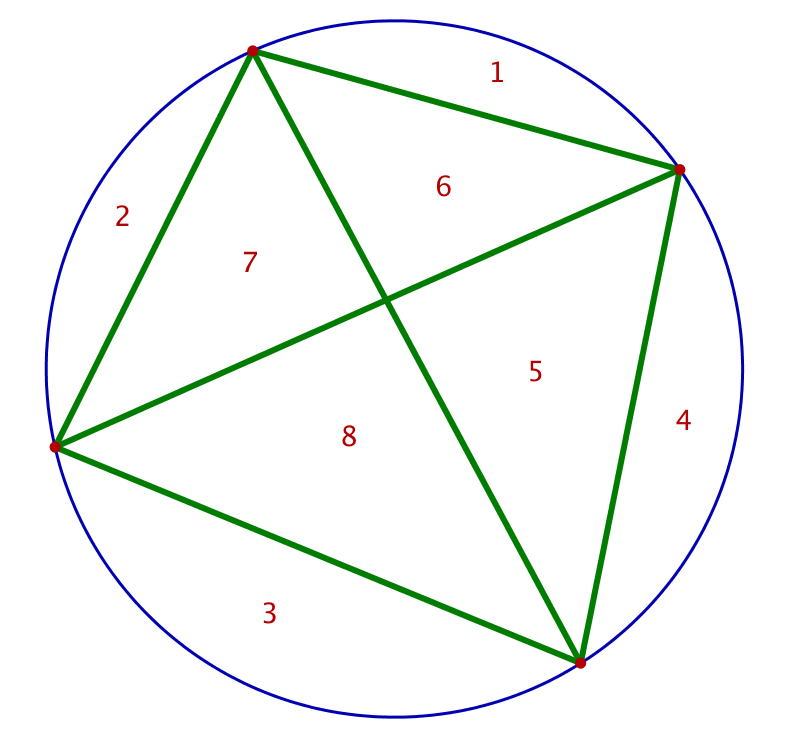
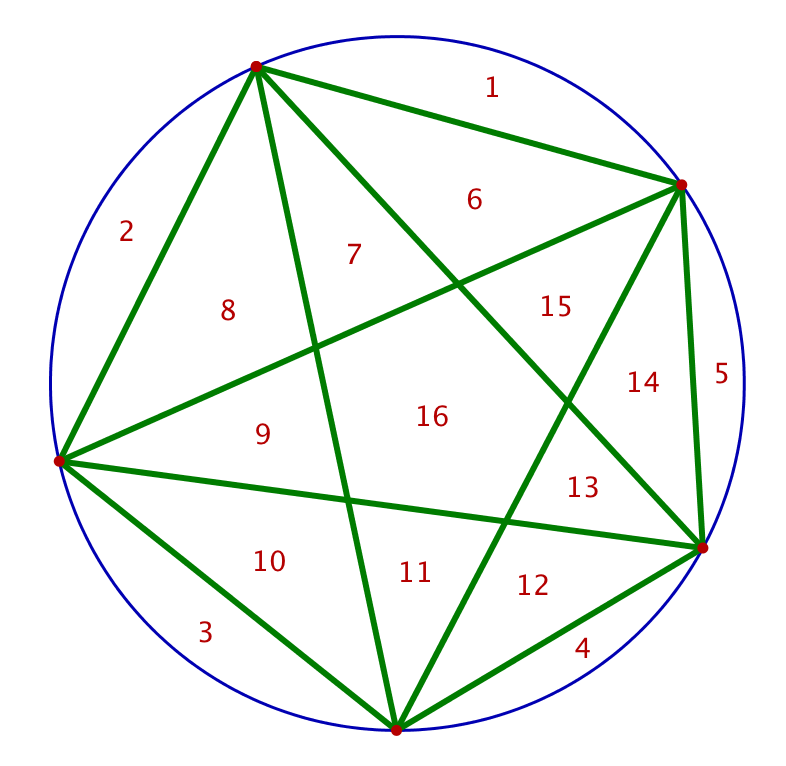
On trouve donc :
![]()
Sauf que cette conjecture est fausse ! En effet, ![]() (et non pas
(et non pas ![]() :
:
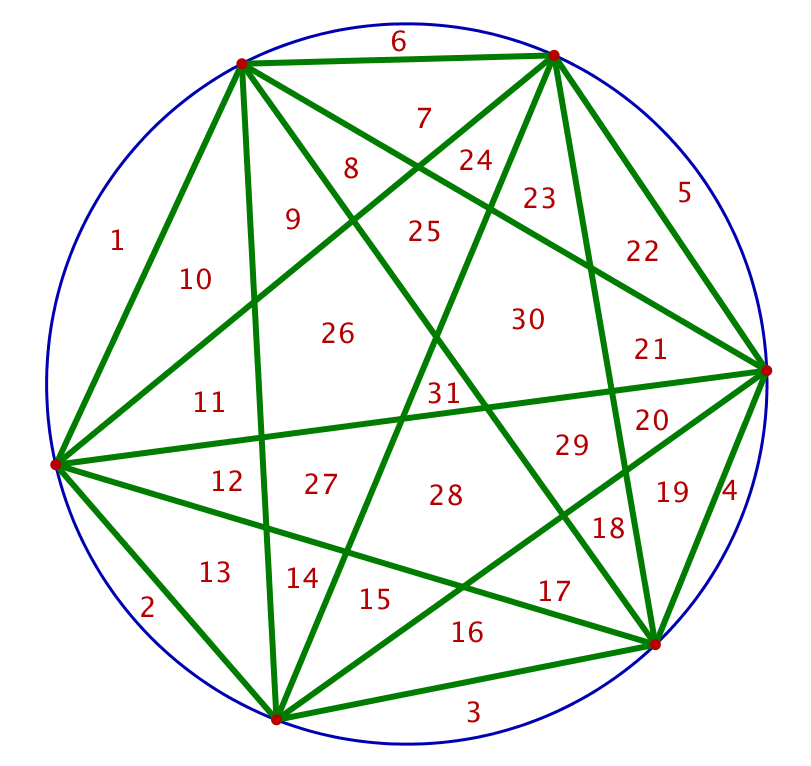
Au fait …
3 – Preuve par récurrence : Comment ça marche ?
On s’intéresse à un énoncé qui fait intervenir un entier naturel ![]() et dont la « valeur de vérité » dépend de
et dont la « valeur de vérité » dépend de ![]() Autrement dit, cet énoncé peut être vrai pour certaines valeurs de
Autrement dit, cet énoncé peut être vrai pour certaines valeurs de ![]() et faux pour d’autres.
et faux pour d’autres.
Par exemple, il pourrait s’agir de :
 : « la somme des
: « la somme des  premiers nombres impairs est un carré parfait »,
premiers nombres impairs est un carré parfait »,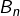 : « le produit de
: « le produit de  entiers consécutifs est multiple de
entiers consécutifs est multiple de 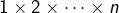 « ,
« ,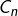 : «
: « 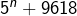 un nombre premier ».
un nombre premier ».
Il se trouve que ![]() est vrai pour tout
est vrai pour tout ![]() (voir section 6 du présent article) et qu’il en va de même pour
(voir section 6 du présent article) et qu’il en va de même pour ![]() (voir l’article Le produit de k entiers consécutifs est multiple de k!).
(voir l’article Le produit de k entiers consécutifs est multiple de k!).
En revanche, ![]() est vrai pour certaines valeurs de
est vrai pour certaines valeurs de ![]() (par exemple tous les entiers de 0 à 10, mais pas seulement : les entiers 13, 17, 18, 19 et 24 conviennent aussi) mais pas pour d’autres.
(par exemple tous les entiers de 0 à 10, mais pas seulement : les entiers 13, 17, 18, 19 et 24 conviennent aussi) mais pas pour d’autres.
Et comme les mathématiques ne sont pas une science facile (ça se saurait…), ne perdons pas de vue qu’il existe des énoncés qui sont vrais pour toutes les valeurs particulières de ![]() qu’on a pu tester, mais dont personne n’est à ce jour capable de démontrer la validité pour tout
qu’on a pu tester, mais dont personne n’est à ce jour capable de démontrer la validité pour tout ![]() Par exemple :
Par exemple :
![]() : Pour tout
: Pour tout ![]() le nombre pair
le nombre pair ![]() est la somme de deux nombres premiers.
est la somme de deux nombres premiers.
Il s’agit de la célèbre conjecture de Goldbach. A ce sujet, le lecteur intéressé pourra consulter l’article Qu’est-ce qu’une conjecture ? mais revenons à nos moutons…
La question centrale est :
Question :
Etant donnés : • un énoncé ![]() portant sur un entier naturel
portant sur un entier naturel ![]() , • un entier naturel
, • un entier naturel ![]() ,
,
Comment peut-on prouver que ![]() est vrai pour tout
est vrai pour tout ![]() ?
?
Le raisonnement par récurrence apporte une réponse. Voici en quoi il consiste :
Réponse
➡ On prouve d’une part que ![]() est vrai.
est vrai.
➡ On prouve d’autre part que, si ![]() est vrai pour un certain
est vrai pour un certain ![]() alors
alors ![]() est aussi vrai.
est aussi vrai.
Le premier point constitue l’initialisation. Le second indique que l’énoncé est héréditaire (c’est-à-dire que sa validité se transmet de chaque entier ![]() à son successeur).
à son successeur).
Intuitivement, comme ![]() est vrai alors
est vrai alors ![]() aussi d’après l’hérédité. Puis, comme
aussi d’après l’hérédité. Puis, comme ![]() est vrai, alors
est vrai, alors ![]() aussi toujours d’après l’hérédité. De même, puisque
aussi toujours d’après l’hérédité. De même, puisque ![]() est vrai, alors
est vrai, alors ![]() aussi … et ainsi de suite …
aussi … et ainsi de suite …
En quelque sorte, l’initialisation constitue un « germe » et l’hérédité permet à ce germe de « s’auto développer » à l’infini.
Il est temps pour nous d’aborder quelques exemples fondamentaux de démonstrations par récurrence.
4 – Notre tout premier exemple
Revenons à la question examinée à la section 1. Il s’agissait de prouver que ![]() est impair, quel que soit l’entier naturel
est impair, quel que soit l’entier naturel ![]()
Pour ![]() c’est vrai ! Ceci règle l’initialisation.
c’est vrai ! Ceci règle l’initialisation.
Et si ![]() est impair pour un certain
est impair pour un certain ![]() alors :
alors :
![]()
Nous disposons donc de deux démonstrations d’un même résultat : directement (cf. section 1) et par récurrence. Passons à un autre exemple.
5 – Un grand classique !
Dans ce qui suit, la somme des entiers de 1 jusqu’à ![]() sera notée
sera notée ![]() Autrement dit :
Autrement dit :
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d413ea005547fe5b3af318bed45f92_l3.png)
Pour commencer, calculons ![]() pour de petites valeurs de
pour de petites valeurs de ![]() :
:
![]()

Avec un peu d’attention, on observe que, par exemple :
![]()
Conjecture
Pour tout ![]() la somme des
la somme des ![]() premiers entiers est
premiers entiers est ![]()
Nous allons maintenant démontrer ceci, par récurrence.
Pour l’initialisation, il s’agit de vérifier que ![]() et c’est bien le cas.
et c’est bien le cas.
Pour l’hérédité, on suppose que ![]() pour un certain
pour un certain ![]() et l’on prouve que, sous cette hypothèse :
et l’on prouve que, sous cette hypothèse : ![]()
Voici comment :
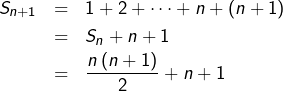
![]()
![]()
Signalons que ce résultat est parfaitement accessible sans récurrence. On raconte que le grand mathématicien allemand Carl Friedrich Gauss découvrit, lorsqu’il était encore enfant, la preuve suivante. Le double de la somme demandée se ré-écrit en associant les termes ![]() et
et ![]() les termes
les termes ![]() et
et ![]() etc … ce qui fait apparaître
etc … ce qui fait apparaître ![]() groupes de deux termes, chaque groupe formant un total de
groupes de deux termes, chaque groupe formant un total de ![]() En symboles :
En symboles :
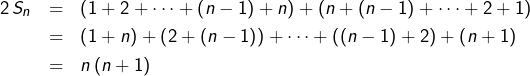
![]()
6 – La somme des n premiers nombres impairs
Le premier nombre impair (positif) est 1. Les trois suivants sont 3, 5 et 7. Quel est le ![]() ème ?
ème ?
Il n’est pas difficile de deviner la formule générale :
Conjecture 1
Pour tout ![]() le
le ![]() ème nombre impair est
ème nombre impair est ![]()
A ce stade, deux situations sont envisageables : si cette affirmation vous paraît évidente, nous allons pouvoir passer directement à la suite ! Et sinon, il va falloir l’établir… par récurrence.
Preuve de la conjecture 1 (cliquer pour déplier / replier)
Notons donc ![]() le
le ![]() ème nombre impair. Il est clair que
ème nombre impair. Il est clair que ![]() ce qui règle la question de l’initialisation. Ensuite, en supposant que
ce qui règle la question de l’initialisation. Ensuite, en supposant que ![]() pour un certain entier
pour un certain entier ![]() on observe que :
on observe que :
![]()
Passons à la question qui nous occupe dans cette section : que vaut la somme des ![]() premiers nombres impairs ?
premiers nombres impairs ?
En la notant ![]() on calcule aisément :
on calcule aisément :
![]()

De toute évidence, ce sont les dix premiers carrés parfaits qui apparaissent ici. On est donc naturellement que conduit à la :
Conjecture 2
Pour tout ![]() la somme des
la somme des ![]() premiers nombres impairs est
premiers nombres impairs est ![]()
Après avoir conjecturé, il faut démontrer. Et vous commencez à connaître la chanson : on va procéder par récurrence.
Preuve de la conjecture 2 (cliquer pour déplier / replier)
Pour l’initialisation, on se borne à observer que :
![]()
Pour l’hérédité, on suppose que ![]() pour un certain
pour un certain ![]() on calcule alors :
on calcule alors :
![]()
Nos connaissances de collège sur les identités remarquables nous permettent de reconnaître que cette dernière quantité n’est autre que ![]()
C’est exactement ce qu’on voulait obtenir.
Notons que, comme pour le résultat établi à la section 5, une preuve directe est envisageable. Il suffit (en utilisant la notation ![]() introduite à la section précédente) d’observer que :
introduite à la section précédente) d’observer que :
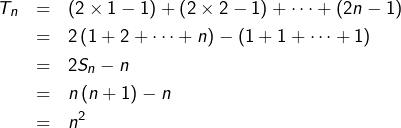
C’est la troisième fois qu’on démontre un résultat par récurrence… pour se rendre compte ensuite qu’on pouvait l’établir directement. Le principal avantage d’une preuve directe est qu’on n’a pas besoin de conjecturer le résultat à démontrer ! Ce résultat apparaît « naturellement », au terme d’un calcul.
Mais le raisonnement par récurrence n’en est pas pour autant inutile ! Dans beaucoup de situations, on ne sait pas vraiment faire autrement. Les deux sections suivantes proposent des exemples de telles situations.
7 – Une identité remarquable
Proposition
Pour tout entier ![]() et tout nombre réel
et tout nombre réel ![]() on a la formule de factorisation :
on a la formule de factorisation :
![]()
Preuve de la proposition (cliquer pour déplier / replier)
Démontrons ceci par récurrence (le réel ![]() étant fixé). Pour
étant fixé). Pour ![]() c’est une égalité bien connue depuis le collège :
c’est une égalité bien connue depuis le collège :
![]()
Supposons l’égalité ![]() vraie pour un certain
vraie pour un certain ![]() alors :
alors :
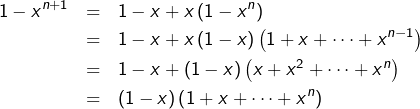
La formule ![]() est fondamentale. Pour
est fondamentale. Pour ![]() elle prend la forme :
elle prend la forme :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{u_{0}+u_{1}+\cdots+u_{n-1}=u_{0}\frac{1-x^{n}}{1-x}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-71e385a9a643acf1ac52d250a71bd0a1_l3.png)
![]()
Passons à un exemple à la fois plus anecdotique et plus élaboré.
8 – Une suite ultimement croissante
Fixons un réel ![]() et considérons la suite
et considérons la suite ![]() définie par :
définie par :
![]()
![]()
![]()
Nous allons prouver que, peu importe la valeur choisie pour ![]() la suite
la suite ![]() est « strictement croissante à partir d’un certain rang », c’est-à-dire :
est « strictement croissante à partir d’un certain rang », c’est-à-dire :
Proposition A
Il existe ![]() tel que
tel que ![]() pour tout
pour tout ![]()
Pour cela, commençons par établir un résultat plus faible, à savoir :
Proposition B
Il existe un entier ![]() tel que
tel que ![]()
Dans le cas contraire, à savoir que ![]() pour tout
pour tout ![]() la suite serait décroissante donc majorée (par
la suite serait décroissante donc majorée (par ![]() ce qui est absurde puisque
ce qui est absurde puisque ![]() pour tout
pour tout ![]() (et ceci impose bien sûr que
(et ceci impose bien sûr que ![]()
Le résultat ![]() est acquis. Montrons maintenant
est acquis. Montrons maintenant ![]() en procédant par récurrence.
en procédant par récurrence.
On sait déjà que ![]() ce qui donne l’initialisation.
ce qui donne l’initialisation.
Supposons que, pour un certain ![]() on ait :
on ait : ![]() Alors :
Alors :
![]()
9 – Une remarque « philosophique » pour conclure
Pour s’assurer de la validité d’un énoncé ![]() quelle que soit la valeur de l’entier naturel
quelle que soit la valeur de l’entier naturel ![]() la première idée qui peut venir à l’esprit est de tester successivement les cas
la première idée qui peut venir à l’esprit est de tester successivement les cas ![]()
![]()
![]() etc…
etc…
Deux problèmes majeurs surviennent :
- L’examen d’un nombre fini de cas ne peut pas suffire (voir la deuxième section du présent article)
- L’examen de tous les cas, un à un, est impossible… puisqu’il en existe une infinité !
La puissance du raisonnement par récurrence apparaît en pleine lumière : on traite une infinité de cas en utilisant seulement un nombre fini de mots !
A méditer …
Je vous remercie d’avoir pris le temps de me lire jusqu’au bout 🙂
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.


Ah oui ! Merci pour cette précision 😊
Bonjour,
Merci pour cet article.
C’est une micro remarque, mais avant la partie 7 vous annoncez des résultats difficilement démontrables par voie directe, mais l’exemple de la partie 7 peut se faire en faisant apparaître une somme télescopique dans le membre de droite ?
Bien à vous.
Vous avez en partie raison. On peut en effet écrire ceci, pour tout réel (ou complexe) et tout entier
et tout entier  :
:
Cela dit, si l’on gratte un peu, comment se démontre la formule des sommes télescopiques ? Par récurrence …